|
List Of Mathematical Topics In Quantum Theory
{{Short description, List article This is a list of mathematical topics in Quantum mechanics, quantum theory, by Wikipedia page. See also list of functional analysis topics, list of Lie group topics, list of quantum-mechanical systems with analytical solutions. Mathematical formulation of quantum mechanics * bra–ket notation * canonical commutation relation * complete set of commuting observables * Heisenberg picture * Hilbert space * Interaction picture * Measurement in quantum mechanics * quantum field theory * quantum logic * quantum operation * Schrödinger picture * semiclassical physics, semiclassical * statistical ensemble * wavefunction * wave–particle duality * Wightman axioms * WKB approximation Schrödinger equation * quantum mechanics, matrix mechanics, Hamiltonian (quantum mechanics) * particle in a box * particle in a ring * particle in a spherically symmetric potential * quantum harmonic oscillator * hydrogen atom * ring wave guide * particle in a one-dimensiona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Ensemble
In physics, specifically statistical mechanics, an ensemble (also statistical ensemble) is an idealization consisting of a large number of virtual copies (sometimes infinitely many) of a system, considered all at once, each of which represents a possible state that the real system might be in. In other words, a statistical ensemble is a set of systems of particles used in statistical mechanics to describe a single system. The concept of an ensemble was introduced by J. Willard Gibbs in 1902. A thermodynamic ensemble is a specific variety of statistical ensemble that, among other properties, is in statistical equilibrium (defined below), and is used to derive the properties of thermodynamic systems from the laws of classical or quantum mechanics. Physical considerations The ensemble formalises the notion that an experimenter repeating an experiment again and again under the same macroscopic conditions, but unable to control the microscopic details, may expect to observe a ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
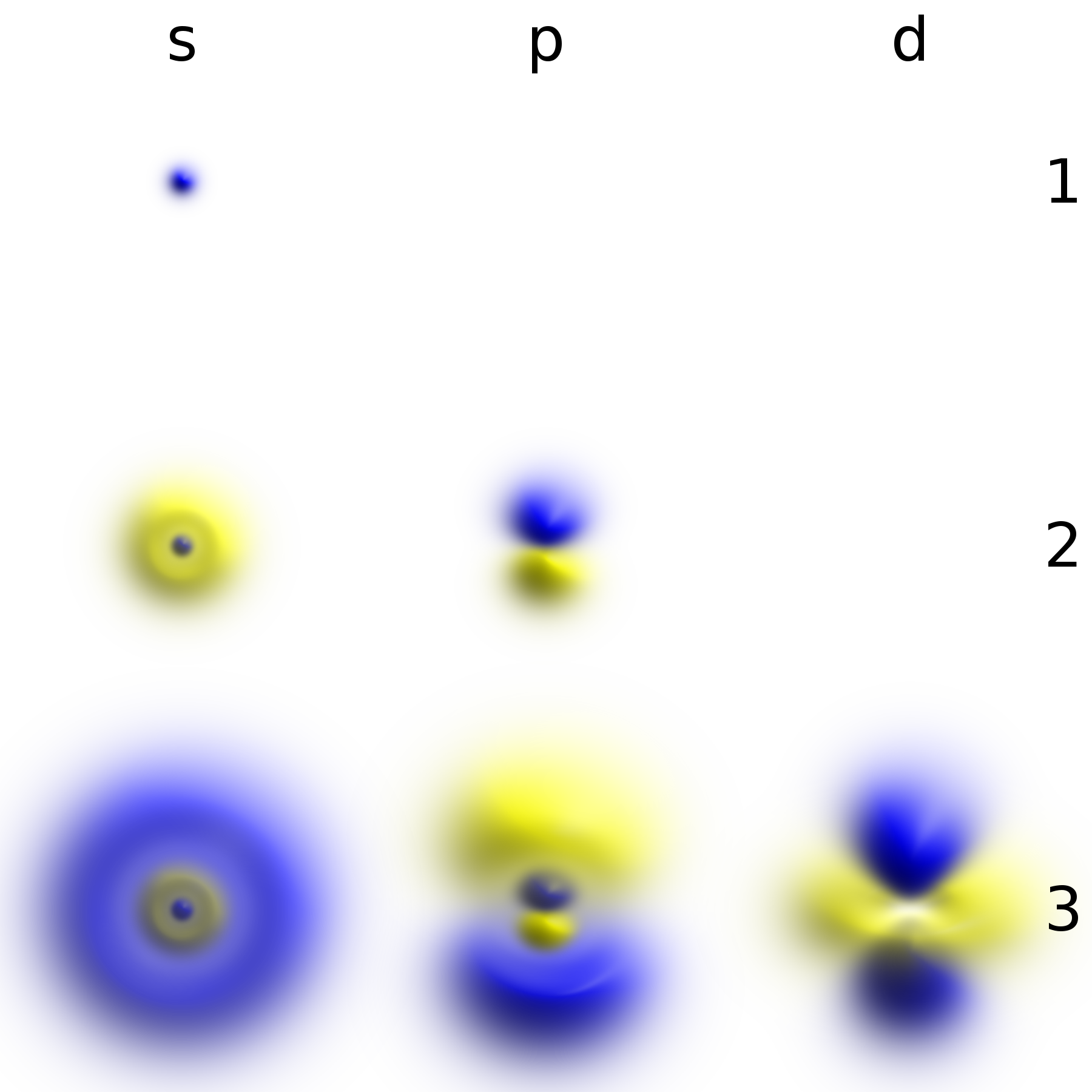
Hydrogen Atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively charged proton and a single negatively charged electron bound to the nucleus by the Coulomb force. Atomic hydrogen constitutes about 75% of the baryonic mass of the universe. In everyday life on Earth, isolated hydrogen atoms (called "atomic hydrogen") are extremely rare. Instead, a hydrogen atom tends to combine with other atoms in compounds, or with another hydrogen atom to form ordinary ( diatomic) hydrogen gas, H2. "Atomic hydrogen" and "hydrogen atom" in ordinary English use have overlapping, yet distinct, meanings. For example, a water molecule contains two hydrogen atoms, but does not contain atomic hydrogen (which would refer to isolated hydrogen atoms). Atomic spectroscopy shows that there is a discrete infinite set of states in which a hydrogen (or any) atom can exist, contrary to the predictions of classical physics. Attempts to develop a th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Harmonic Oscillator
量子調和振動子 は、調和振動子, 古典調和振動子 の 量子力学, 量子力学 類似物です。任意の滑らかな ポテンシャル エネルギー, ポテンシャル は通常、安定した 平衡点 の近くで 調和振動子#単純調和振動子, 調和ポテンシャル として近似できるため、最も量子力学における重要なモデル系。さらに、これは正確な量子力学システムのリスト, 解析解法が知られている数少ない量子力学系の1つである。 author=Griffiths, David J. , title=量子力学入門 , エディション=2nd , 出版社=プレンティス・ホール , 年=2004 , isbn=978-0-13-805326-0 , author-link=David Griffiths (物理学者) , URL アクセス = 登録 , url=https://archive.org/details/introductiontoel00grif_0 One-dimensional harmonic oscillator Hamiltonian and energy eigenstates 粒子の ハミルトニアン (量子力学), ハミルトニアン は次の� ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle In A Spherically Symmetric Potential
In the quantum mechanics description of a particle in spherical coordinates, a spherically symmetric potential, is a potential that depends only on the distance between the particle and a defined centre point. One example of a spherical potential is the electron within a hydrogen atom. The electron's potential depends only on its distance from the proton in the atom's nucleus. This spherical potential can be derived from Coulomb's law. In the general case, the dynamics of a particle in a spherically symmetric potential are governed by a Hamiltonian of the following form: \hat = \frac + V(r) Where m_0 is the mass of the particle, \hat is the momentum operator, and the potential V(r) depends only on r, the modulus of the radius vector. The possible quantum states of the particle are found by using the above Hamiltonian to solve the Schrödinger equation for its eigenvalues, which are wave functions. To describe these spherically symmetric systems, it is natural to use ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle In A Ring
In quantum mechanics, the case of a particle in a one-dimensional ring is similar to the particle in a box. The Schrödinger equation for a free particle which is restricted to a ring (technically, whose configuration space is the circle S^1) is : -\frac\nabla^2 \psi = E\psi Wave function Using polar coordinates on the 1-dimensional ring of radius R, the wave function depends only on the angular coordinate, and so Problems and Solutions to accompany Physical Chemistry: a Molecular Approach : \nabla^2 = \frac \frac Requiring that the wave function be periodic in \ \theta with a period 2 \pi (from the demand that the wave functions be single-valued functions on the circle), and that they be normalized leads to the conditions : \int_^ \left, \psi ( \theta ) \^2 \, d\theta = 1\ , and : \ \psi (\theta) = \ \psi ( \theta + 2\pi) Under these conditions, the solution to the Schrödinger equation is given by : \psi_(\theta) = \frac\, e^ Energy eigenvalues The energy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle In A Box
In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems. In classical systems, for example, a particle trapped inside a large box can move at any speed within the box and it is no more likely to be found at one position than another. However, when the well becomes very narrow (on the scale of a few nanometers), quantum effects become important. The particle may only occupy certain positive energy levels. Likewise, it can never have zero energy, meaning that the particle can never "sit still". Additionally, it is more likely to be found at certain positions than at others, depending on its energy level. The particle may never be detected at certain positions, known as spatial nodes. The particle in a box mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
Hamiltonian may refer to: * Hamiltonian mechanics, a function that represents the total energy of a system * Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system ** Dyall Hamiltonian, a modified Hamiltonian with two-electron nature ** Molecular Hamiltonian, the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule * Hamiltonian (control theory), a function used to solve a problem of optimal control for a dynamical system * Hamiltonian path, a path in a graph that visits each vertex exactly once * Hamiltonian group, a non-abelian group the subgroups of which are all normal * Hamiltonian economic program, the economic policies advocated by Alexander Hamilton, the first United States Secretary of the Treasury See also * Alexander Hamilton (1755 or 1757–1804), American statesman and one of the Founding Fathers of the US * Hamilton (other) * List of things named after William Rowan Hamilton {{ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Mechanics
Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925. It was the first conceptually autonomous and logically consistent formulation of quantum mechanics. Its account of quantum jumps supplanted the Bohr model's electron orbits. It did so by interpreting the physical properties of particles as matrices that evolve in time. It is equivalent to the Schrödinger wave formulation of quantum mechanics, as manifest in Dirac's bra–ket notation. In some contrast to the wave formulation, it produces spectra of (mostly energy) operators by purely algebraic, ladder operator methods. Relying on these methods, Wolfgang Pauli derived the hydrogen atom spectrum in 1926, before the development of wave mechanics. Development of matrix mechanics In 1925, Werner Heisenberg, Max Born, and Pascual Jordan formulated the matrix mechanics representation of quantum mechanics. Epiphany at Helgoland In 1925 Werner Heisenberg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Schrödinger Equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933. Conceptually, the Schrödinger equation is the quantum counterpart of Newton's second law in classical mechanics. Given a set of known initial conditions, Newton's second law makes a mathematical prediction as to what path a given physical system will take over time. The Schrödinger equation gives the evolution over time of a wave function, the quantum-mechanical characterization of an isolated physical system. The equation can be derived from the fact that the time-evolution operator must be unitary, and must therefore be generated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
WKB Approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear differential equations with spatially varying coefficients. It is typically used for a semiclassical calculation in quantum mechanics in which the wavefunction is recast as an exponential function, semiclassically expanded, and then either the amplitude or the phase is taken to be changing slowly. The name is an initialism for Wentzel–Kramers–Brillouin. It is also known as the LG or Liouville–Green method. Other often-used letter combinations include JWKB and WKBJ, where the "J" stands for Jeffreys. Brief history This method is named after physicists Gregor Wentzel, Hendrik Anthony Kramers, and Léon Brillouin, who all developed it in 1926. In 1923, mathematician Harold Jeffreys had developed a general method of approximating solutions to linear, second-order differential equations, a class that includes the Schrödinger equation. The Schrödinger equat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |




.png)