|
Lindenmayer System
An L-system or Lindenmayer system is a parallel rewriting system and a type of formal grammar. An L-system consists of an alphabet of symbols that can be used to make strings, a collection of production rules that expand each symbol into some larger string of symbols, an initial "axiom" string from which to begin construction, and a mechanism for translating the generated strings into geometric structures. L-systems were introduced and developed in 1968 by Aristid Lindenmayer, a Hungarian theoretical biologist and botanist at the University of Utrecht. Lindenmayer used L-systems to describe the behaviour of plant cells and to model the growth processes of plant development. L-systems have also been used to model the morphology of a variety of organisms and can be used to generate self-similar fractals. Origins As a biologist, Lindenmayer worked with yeast and filamentous fungi and studied the growth patterns of various types of bacteria, such as the cyanobacteria '' Anabaena ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dragon Trees
A dragon is a Magic (supernatural), magical legendary creature that appears in the folklore of multiple cultures worldwide. Beliefs about dragons vary considerably through regions, but European dragon, dragons in Western cultures since the High Middle Ages have often been depicted as winged, horned, and capable of breathing fire. Chinese dragon, Dragons in eastern cultures are usually depicted as wingless, four-legged, Snake, serpentine creatures with above-average intelligence. Commonalities between dragons' traits are often a hybridization of Reptile, reptilian, mammalian, and Bird, avian features. Etymology The word ''dragon'' entered the English language in the early 13th century from Old French , which, in turn, comes from Latin (genitive ), meaning "huge serpent, dragon", from , (genitive , ) "serpent". [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
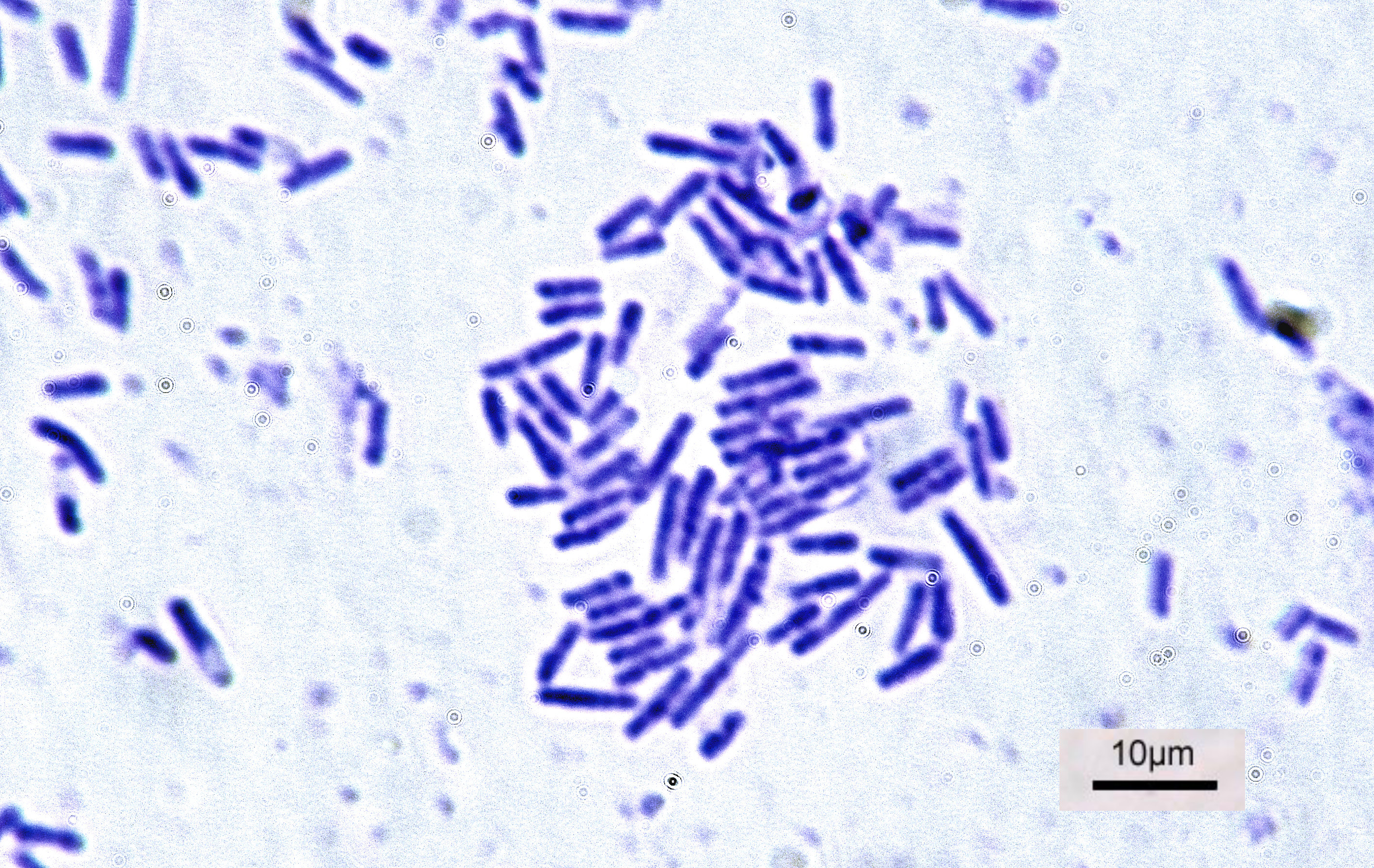
Bacteria
Bacteria (; : bacterium) are ubiquitous, mostly free-living organisms often consisting of one Cell (biology), biological cell. They constitute a large domain (biology), domain of Prokaryote, prokaryotic microorganisms. Typically a few micrometres in length, bacteria were among the first life forms to appear on Earth, and are present in most of its habitats. Bacteria inhabit the air, soil, water, Hot spring, acidic hot springs, radioactive waste, and the deep biosphere of Earth's crust. Bacteria play a vital role in many stages of the nutrient cycle by recycling nutrients and the nitrogen fixation, fixation of nitrogen from the Earth's atmosphere, atmosphere. The nutrient cycle includes the decomposition of cadaver, dead bodies; bacteria are responsible for the putrefaction stage in this process. In the biological communities surrounding hydrothermal vents and cold seeps, extremophile bacteria provide the nutrients needed to sustain life by converting dissolved compounds, suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turtle Graphics
In computer graphics, turtle graphics are vector graphics using a relative cursor (the "turtle") upon a Cartesian plane (x and y axis). Turtle graphics is a key feature of the Logo programming language. It is also a simple and didactic way of dealing with moving frames. Overview The turtle has three attributes: a location, an orientation (or direction), and a pen. The pen, too, has attributes: color, width, and on/off state (also called ''down'' and ''up''). The turtle moves with commands that are relative to its own position, such as "move forward 10 spaces" and "turn left 90 degrees". The pen carried by the turtle can also be controlled, by enabling it, setting its color, or setting its width. A student could understand (and predict and reason about) the turtle's motion by imagining what they would do if they were the turtle. Seymour Papert called this "body syntonic" reasoning. A full turtle graphics system requires control flow, procedures, and recursion: many turtl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractint
Fractint (originally FRACT386) is a freeware computer program to render and display many kinds of fractals. The program originated on MS-DOS, then was ported to the Atari ST, Linux, and Macintosh. During the early 1990s, Fractint was the definitive fractal generating program for personal computers. The name is a portmanteau of ''fractal'' and ''integer'', since the first versions of Fractint used only integer arithmetic (also known as fixed-point arithmetic), for faster rendering on computers without math coprocessors. Since then, floating-point arithmetic and arbitrary-precision arithmetic modes have been added. FractInt can draw most kinds of fractals that have appeared in the literature. It also has a few "fractal types" that are not strictly speaking fractals, but may be more accurately described as display hacks. These include cellular automata. Development Fractint originally appeared in 1988 as FRACT386, a computer program for rendering fractals very quickly on the I ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
D0L System
In mathematics and computer science, a morphic word or substitutive word is an infinite sequence of symbols which is constructed from a particular class of endomorphism of a free monoid. Every automatic sequence is morphic. Definition Let ''f'' be an endomorphism of the free monoid ''A''∗ on an alphabet ''A'' with the property that there is a letter ''a'' such that ''f''(''a'') = ''as'' for a non-empty string ''s'': we say that ''f'' is prolongable at ''a''. The word : a s f(s) f(f(s)) \cdots f^(s) \cdots \ is a pure morphic or pure substitutive word. Note that it is the limit of the sequence ''a'', ''f''(''a''), ''f''(''f''(''a'')), ''f''(''f''(''f''(''a''))), ... It is clearly a fixed point of the endomorphism ''f'': the unique such sequence beginning with the letter ''a''.Lothaire (2011) p. 10Honkala (2010) p.505 In general, a morphic word is the image of a pure morphic word under a coding, that is, a morphism that maps letter to letter. If a morphic word is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Context-free Grammar
In formal language theory, a context-free grammar (CFG) is a formal grammar whose production rules can be applied to a nonterminal symbol regardless of its context. In particular, in a context-free grammar, each production rule is of the form : A\ \to\ \alpha with A a ''single'' nonterminal symbol, and \alpha a string of terminals and/or nonterminals (\alpha can be empty). Regardless of which symbols surround it, the single nonterminal A on the left hand side can always be replaced by \alpha on the right hand side. This distinguishes it from a context-sensitive grammar, which can have production rules in the form \alpha A \beta \rightarrow \alpha \gamma \beta with A a nonterminal symbol and \alpha, \beta, and \gamma strings of terminal and/or nonterminal symbols. A formal grammar is essentially a set of production rules that describe all possible strings in a given formal language. Production rules are simple replacements. For example, the first rule in the picture, : \lan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Language
In logic, mathematics, computer science, and linguistics, a formal language is a set of strings whose symbols are taken from a set called "alphabet". The alphabet of a formal language consists of symbols that concatenate into strings (also called "words"). Words that belong to a particular formal language are sometimes called ''well-formed words''. A formal language is often defined by means of a formal grammar such as a regular grammar or context-free grammar. In computer science, formal languages are used, among others, as the basis for defining the grammar of programming languages and formalized versions of subsets of natural languages, in which the words of the language represent concepts that are associated with meanings or semantics. In computational complexity theory, decision problems are typically defined as formal languages, and complexity classes are defined as the sets of the formal languages that can be parsed by machines with limited computational power. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Law Of Identity
In logic, the law of identity states that each thing is identical with itself. It is the first of the traditional three laws of thought, along with the law of noncontradiction, and the law of excluded middle. However, few systems of logic are built on just these laws. History Ancient philosophy The earliest recorded use of the law appears in Plato's dialogue '' Theaetetus'' (185a), wherein Socrates attempts to establish that what we call "sounds" and "colours" are two different classes of thing: It is used explicitly only once in Aristotle, in a proof in the '' Prior Analytics'': Medieval philosophy Aristotle believed the law of non-contradiction to be the most fundamental law. Both Thomas Aquinas (''Met.'' IV, lect. 6) and Duns Scotus (''Quaest. sup. Met.'' IV, Q. 3) follow Aristotle in this respect. Antonius Andreas, the Spanish disciple of Scotus (d. 1320), argues that the first place should belong to the law "Every Being is a Being" (''Omne Ens est Ens'', Qq. in Met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tuple
In mathematics, a tuple is a finite sequence or ''ordered list'' of numbers or, more generally, mathematical objects, which are called the ''elements'' of the tuple. An -tuple is a tuple of elements, where is a non-negative integer. There is only one 0-tuple, called the ''empty tuple''. A 1-tuple and a 2-tuple are commonly called a singleton and an ordered pair, respectively. The term ''"infinite tuple"'' is occasionally used for ''"infinite sequences"''. Tuples are usually written by listing the elements within parentheses "" and separated by commas; for example, denotes a 5-tuple. Other types of brackets are sometimes used, although they may have a different meaning. An -tuple can be formally defined as the image of a function that has the set of the first natural numbers as its domain. Tuples may be also defined from ordered pairs by a recurrence starting from an ordered pair; indeed, an -tuple can be identified with the ordered pair of its first elements and its t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chomsky Hierarchy
The Chomsky hierarchy in the fields of formal language theory, computer science, and linguistics, is a containment hierarchy of classes of formal grammars. A formal grammar describes how to form strings from a formal language's alphabet that are valid according to the language's syntax. The linguist Noam Chomsky theorized that four different classes of formal grammars existed that could generate increasingly complex languages. Each class can also completely generate the language of all inferior classes (set inclusive). History The general idea of a hierarchy of grammars was first described by Noam Chomsky in "Three models for the description of language" during the formalization of transformational-generative grammar (TGG). Marcel-Paul Schützenberger also played a role in the development of the theory of formal languages; the paper "The algebraic theory of context free languages" describes the modern hierarchy, including context-free grammars. Independently, alongside linguis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Semi-Thue Grammar
In theoretical computer science and mathematical logic a string rewriting system (SRS), historically called a semi-Thue system, is a rewriting system over strings from a (usually finite) alphabet. Given a binary relation R between fixed strings over the alphabet, called rewrite rules, denoted by s\rightarrow t, an SRS extends the rewriting relation to all strings in which the left- and right-hand side of the rules appear as substrings, that is usv\rightarrow utv, where s, t, u, and v are strings. The notion of a semi-Thue system essentially coincides with the presentation of a monoid. Thus they constitute a natural framework for solving the word problem for monoids and groups. An SRS can be defined directly as an abstract rewriting system. It can also be seen as a restricted kind of a term rewriting system, in which all function symbols have an arity of at most 1. As a formalism, string rewriting systems are Turing complete. The semi-Thue name comes from the Norwegian mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artificial Life
Artificial life (ALife or A-Life) is a field of study wherein researchers examine systems related to natural life, its processes, and its evolution, through the use of simulations with computer models, robotics, and biochemistry. The discipline was named by Christopher Langton, an American computer scientist, in 1986. In 1987, Langton organized the first conference on the field, in Los Alamos, New Mexico. There are three main kinds of alife, named for their approaches: ''soft'', from software; ''hard'', from computer hardware, hardware; and ''wet artificial life, wet'', from biochemistry. Artificial life researchers study traditional biology by trying to recreate aspects of biological phenomena. Overview Artificial life studies the fundamental processes of living systems in artificial environments in order to gain a deeper understanding of the complex information processing that define such systems. These topics are broad, but often include Evolutionary algorithm, evolutionar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |