|
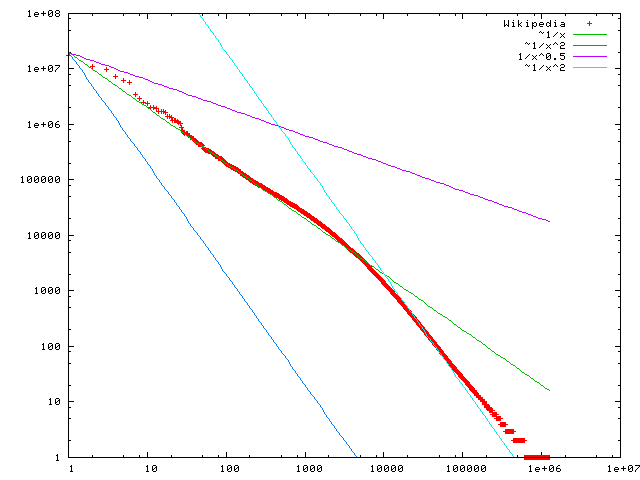
King Effect
In statistics, economics, and econophysics, the king effect is the phenomenon in which the top one or two members of a ranked set show up as clear outliers. These top one or two members are unexpectedly large because they do not conform to the statistical distribution or rank-distribution which the remainder of the set obeys. Distributions typically followed include the power-law distribution, that is a basis for the stretched exponential function, and parabolic fractal distribution. The King effect has been observed in the distribution of: * French city sizes (where the point representing Paris is the "king", failing to conform to the stretched exponential), and similarly for other countries with a primate city, such as the United Kingdom (London), and the extreme case of Bangkok (see list of cities in Thailand). * Country populations (where only the points representing China and India fail to fit a stretched exponential). Note, however, that the king effect is not limited ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank Order Countries
A rank is a position in a hierarchy. It can be formally recognized—for example, cardinal, chief executive officer, general, professor—or unofficial. People Formal ranks * Academic rank * Corporate title * Diplomatic rank * Hierarchy of the Catholic Church * Imperial, royal and noble ranks * Military rank * Police rank Unofficial ranks * Social class * Social position * Social status Either * Seniority Mathematics * Rank (differential topology) * Rank (graph theory) * Rank (linear algebra), the dimension of the vector space generated (or spanned) by a matrix's columns * Rank (set theory) * Rank (type theory) * Rank of an abelian group, the cardinality of a maximal linearly independent subset * Rank of a free module * Rank of a greedoid, the maximal size of a feasible set * Rank of a group, the smallest cardinality of a generating set for the group * Rank of a Lie group – see Cartan subgroup * Rank of a matroid, the maximal size of an independent set * Rank of a pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabolic Fractal Distribution
Parabolic usually refers to something in a shape of a parabola, but may also refer to a parable. Parabolic may refer to: *In mathematics: **In elementary mathematics, especially elementary geometry: **Parabolic coordinates **Parabolic cylindrical coordinates **Möbius transformation#Parabolic transforms, parabolic Möbius transformation **Parabolic geometry (other) **Fermat's spiral, Parabolic spiral **Parabolic line **In advanced mathematics: ***Parabolic cylinder function ***Parabolic induction ***Parabolic Lie algebra ***Parabolic partial differential equation *In physics: **Parabolic trajectory *In technology: **Parabolic antenna **Parabolic microphone **Parabolic reflector **Parabolic trough - a type of solar thermal energy collector **Parabolic flight - a way of achieving weightlessness **Fishing rod#Specifications, Parabolic action, or parabolic bending curve - a term often used to refer to a progressive bending curve in fishing rods. *In commodities and stock market ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Didier Sornette
Didier Sornette (born 25 June 1957 in Paris) is a French researcher studying subjects including complex systems and risk management. He is Professor on the Chair of Entrepreneurial Risks at the ETH Zurich, Swiss Federal Institute of Technology Zurich (ETH Zurich) and is also a professor of the Swiss Finance Institute, He was previously a Professor of Geophysics at UCLA, Los Angeles California (1996–2006) and a Research Professor at the French National Centre for Scientific Research (1981–2006). Theory of earthquakes and fault networks With his long-time collaborator Dr. Guy Ouillon, Sornette has been leading a research group on the “Physics of earthquakes” over the last 25 years. The group is active in the modelling of earthquakes, landslides, and other natural hazards, combining concepts and tools from statistical physics, statistics, tectonics, seismology and more. First located at the Laboratory of Condensed Matter Physics (University of Nice, France), then at the Eart ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zipf's Law
Zipf's law (; ) is an empirical law stating that when a list of measured values is sorted in decreasing order, the value of the -th entry is often approximately inversely proportional to . The best known instance of Zipf's law applies to the frequency table of words in a text or corpus of natural language: \ \mathsf\ \propto\ \frac ~. It is usually found that the most common word occurs approximately twice as often as the next common one, three times as often as the third most common, and so on. For example, in the Brown Corpus of American English text, the word "''the''" is the most frequently occurring word, and by itself accounts for nearly 7% of all word occurrences (69,971 out of slightly over 1 million). True to Zipf's law, the second-place word "''of''" accounts for slightly over 3.5% of words (36,411 occurrences), followed by "''and''" (28,852). It is often used in the following form, called Zipf-Mandelbrot law: \ \mathsf\ \propto\ \frac\ where \ a\ a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Countries And Dependencies By Population
This is a list of countries and dependencies by population. It includes sovereign states, inhabited dependent territories and, in some cases, constituent countries of sovereign states, with inclusion within the list being primarily based on the ISO standard ISO 3166-1. For instance, the United Kingdom is considered a single entity, while the constituent countries of the Kingdom of the Netherlands are considered separately. In addition, this list includes certain states with limited recognition not found in ISO 3166-1. Also given in a percentage is each country's population compared with the world population, which the United Nations estimated at 8.232 billion as of 2025. Method Figures used in this chart are based on the most up-to-date estimates or projections by the national census authority, where available, and are usually rounded off. Where updated national data are not available, figures are based on the estimates or projections for 2024 by the Population Divisi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Cities In Thailand
Thailand divides its settlements (''thesaban'') into three categories by size: city municipalities (''thesaban nakhon''), towns (''thesaban mueang'') and townships (or subdistrict municipality) (''thesaban tambon''). There are 33 city municipalities as of November 2024. The national capital Bangkok and the special governed city Pattaya fall outside these divisions. They are "self-governing districts". Due to the outdated nature of the ''thesaban'' system, any city municipality's growth subsequent to its settlement designation is not included in both area and population numbers. For this reason, the Department of Public Works and Town & Country Planning, and each province's Provincial Administrative Organization regularly revise and publish up-to-date city boundaries () to reflect population growth. These revisions are royally decreed and published in the ''Royal Gazette (Thailand), Royal Thai Government Gazette''. The term เขตเมือง/''khet mueang'' can also be tran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bangkok
Bangkok, officially known in Thai language, Thai as Krung Thep Maha Nakhon and colloquially as Krung Thep, is the capital and most populous city of Thailand. The city occupies in the Chao Phraya River delta in central Thailand and has an estimated population of 10 million people as of 2024, 13% of the country's population. Over 17.4 million people (25% of Thailand's population) live within the surrounding Bangkok Metropolitan Region as of the 2021 estimate, making Bangkok a megacity and an extreme primate city, dwarfing Thailand's other urban centres in both size and importance to the national economy. Bangkok traces its roots to a small trading post during the Ayutthaya Kingdom, Ayutthaya era in the 15th century, which eventually grew and became the site of two capital cities, Thonburi Kingdom, Thonburi in 1767 and Rattanakosin Kingdom (1782–1932), Rattanakosin in 1782. Bangkok was at the heart of the modernization of Siam during the late 19th century, as the count ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Primate City
A primate city is a city that is the largest in its country, province, state, or region, and disproportionately larger than any others in the urban hierarchy. A ''primate city distribution'' is a rank-size distribution that has one very large city with many much smaller cities and towns and no intermediate-sized urban centers, creating a statistical king effect. The ''law of the primate city'' was first proposed by the geographer Mark Jefferson in 1939. He defines a primate city as being "at least twice as large as the next largest city and more than twice as significant." Aside from size and population, a primate city will usually have precedence in all other aspects of its country's society such as economics, politics, culture, and education. Primate cities also serve as targets for the majority of a country or region's internal migration. In geography, the phenomenon of excessive concentration of population and development of the main city of a country or a region (often ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stretched Exponential Function
The stretched exponential function f_\beta (t) = e^ is obtained by inserting a fractional power law into the exponential function. In most applications, it is meaningful only for arguments between 0 and +∞. With , the usual exponential function is recovered. With a ''stretching exponent'' ''β'' between 0 and 1, the graph of log ''f'' versus ''t'' is characteristically ''stretched'', hence the name of the function. The compressed exponential function (with ) has less practical importance, with the notable exceptions of , which gives the normal distribution In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac ..., and of compressed exponential relaxation in the dynamics of amorphous solids. In mathematics, the stretched exponential is also known as the Cumulative distribution fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a relative change in the other quantity proportional to the change raised to a constant exponent: one quantity varies as a power of another. The change is independent of the initial size of those quantities. For instance, the area of a square has a power law relationship with the length of its side, since if the length is doubled, the area is multiplied by 2, while if the length is tripled, the area is multiplied by 3, and so on. Empirical examples The distributions of a wide variety of physical, biological, and human-made phenomena approximately follow a power law over a wide range of magnitudes: these include the sizes of craters on the moon and of solar flares, cloud sizes, the foraging pattern of various species, the sizes of activity patterns of neuronal populations, the frequencies of words ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rank–size Distribution
Rank–size distribution is the distribution of size by rank, in decreasing order of size. For example, if a data set consists of items of sizes 5, 100, 5, and 8, the rank-size distribution is 100, 8, 5, 5 (ranks 1 through 4). This is also known as the rank–frequency distribution, when the source data are from a frequency distribution. These are particularly of interest when the data vary significantly in scales, such as city size or word frequency. These distributions frequently follow a power law distribution, or less well-known ones such as a stretched exponential function or parabolic fractal distribution, at least approximately for certain ranges of ranks; see below. A rank-size distribution is not a probability distribution or cumulative distribution function. Rather, it is a discrete form of a quantile function (inverse cumulative distribution) in reverse order, giving the size of the element at a given rank. Simple rank–size distributions In the case of city populati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |