RankŌĆōsize Distribution on:
[Wikipedia]
[Google]
[Amazon]
 RankŌĆōsize distribution is the distribution of size by rank, in decreasing order of size. For example, if a data set consists of items of sizes 5, 100, 5, and 8, the rank-size distribution is 100, 8, 5, 5 (ranks 1 through 4). This is also known as the rankŌĆōfrequency distribution, when the source data are from a
RankŌĆōsize distribution is the distribution of size by rank, in decreasing order of size. For example, if a data set consists of items of sizes 5, 100, 5, and 8, the rank-size distribution is 100, 8, 5, 5 (ranks 1 through 4). This is also known as the rankŌĆōfrequency distribution, when the source data are from a
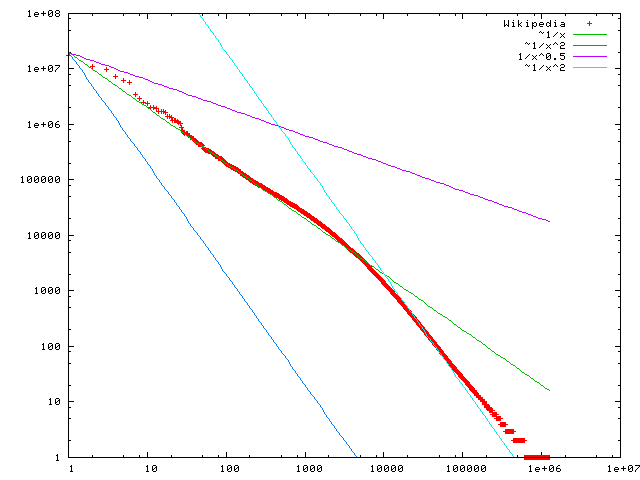 A rank-size (or rankŌĆōfrequency) distribution is often segmented into ranges. This is frequently done somewhat arbitrarily or due to external factors, particularly for
A rank-size (or rankŌĆōfrequency) distribution is often segmented into ranges. This is frequently done somewhat arbitrarily or due to external factors, particularly for
Rand Fishkin, November 24th, 2009 also belly,Digg that Fat Belly!
Robert Young, Sep. 4, 2006 torso, and body.The Small Head, the Medium Body, and the Long Tail .. so, where's Microsoft?
, 12 Mar 2005, Lawrence Liu's Report from the Inside These frequently have some adjectives added, most significantly ''
The Use of Agent-Based Models in Regional Science
Ćöan agent-based simulation study that explains rankŌĆōsize distribution.
 RankŌĆōsize distribution is the distribution of size by rank, in decreasing order of size. For example, if a data set consists of items of sizes 5, 100, 5, and 8, the rank-size distribution is 100, 8, 5, 5 (ranks 1 through 4). This is also known as the rankŌĆōfrequency distribution, when the source data are from a
RankŌĆōsize distribution is the distribution of size by rank, in decreasing order of size. For example, if a data set consists of items of sizes 5, 100, 5, and 8, the rank-size distribution is 100, 8, 5, 5 (ranks 1 through 4). This is also known as the rankŌĆōfrequency distribution, when the source data are from a frequency distribution
In statistics, the frequency or absolute frequency of an Event (probability theory), event i is the number n_i of times the observation has occurred/been recorded in an experiment or study. These frequencies are often depicted graphically or tabu ...
. These are particularly of interest when the data vary significantly in scales, such as city size or word frequency. These distributions frequently follow a power law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a relative change in the other quantity proportional to the ...
distribution, or less well-known ones such as a stretched exponential function or parabolic fractal distribution
Parabolic usually refers to something in a shape of a parabola, but may also refer to a parable.
Parabolic may refer to:
*In mathematics:
**In elementary mathematics, especially elementary geometry:
**Parabolic coordinates
**Parabolic cylindrical ...
, at least approximately for certain ranges of ranks; see below.
A rank-size distribution is not a probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
or cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
. Rather, it is a discrete form of a quantile function
In probability and statistics, the quantile function is a function Q: ,1\mapsto \mathbb which maps some probability x \in ,1/math> of a random variable v to the value of the variable y such that P(v\leq y) = x according to its probability distr ...
(inverse cumulative distribution) in reverse order, giving the size of the element at a given rank.
Simple rankŌĆōsize distributions
In the case of city populations, the resulting distribution in a country, a region, or the world will be characterized by its largest city, with other cities decreasing in size respective to it, initially at a rapid rate and then more slowly. This results in a few large cities and a much larger number of cities orders of magnitude smaller. For example, a rank 3 city would have one-third the population of a country's largest city, a rank 4 city would have one-fourth the population of the largest city, and so on.Segmentation
 A rank-size (or rankŌĆōfrequency) distribution is often segmented into ranges. This is frequently done somewhat arbitrarily or due to external factors, particularly for
A rank-size (or rankŌĆōfrequency) distribution is often segmented into ranges. This is frequently done somewhat arbitrarily or due to external factors, particularly for market segmentation
In marketing, market segmentation or customer segmentation is the process of dividing a consumer or business market into meaningful sub-groups of current or potential customers (or consumers) known as ''segments''. Its purpose is to identify pr ...
, but can also be due to distinct behavior as rank varies.
Most simply and commonly, a distribution may be split in two pieces, termed the head and tail. If a distribution is broken into three pieces, the third (middle) piece has several terms, generically middle,Illustrating the Long TailRand Fishkin, November 24th, 2009 also belly,Digg that Fat Belly!
Robert Young, Sep. 4, 2006 torso, and body.The Small Head, the Medium Body, and the Long Tail .. so, where's Microsoft?
, 12 Mar 2005, Lawrence Liu's Report from the Inside These frequently have some adjectives added, most significantly ''
long tail
In statistics and business, a long tail of some distributions of numbers is the portion of the distribution having many occurrences far from the "head" or central part of the distribution. The distribution could involve popularities, random n ...
'', also ''fat belly'', ''chunky middle'', etc. In more traditional terms, these may be called ''top-tier'', ''mid-tier'', and ''bottom-tier''.
The relative sizes and weights of these segments (how many ranks in each segment, and what proportion of the total population is in a given segment) qualitatively characterize a distribution, analogously to the skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined.
For a unimodal ...
or kurtosis
In probability theory and statistics, kurtosis (from , ''kyrtos'' or ''kurtos'', meaning "curved, arching") refers to the degree of ŌĆ£tailednessŌĆØ in the probability distribution of a real-valued random variable. Similar to skewness, kurtos ...
of a probability distribution. Namely: is it dominated by a few top members (head-heavy, like profits in the recorded music industry), or is it dominated by many small members (tail-heavy, like internet search queries), or distributed in some other way? Practically, this determines strategy: where should attention be focused?
These distinctions may be made for various reasons. For example, they may arise from differing properties of the population, as in the 90ŌĆō9ŌĆō1 principle, which posits that in an internet community, 90% of the participants of a community only view content, 9% of the participants edit content, and 1% of the participants actively create new content. As another example, in marketing, one may pragmatically consider the head as all members that receive personalized attention, such as personal phone calls; while the tail is everything else, which does not receive personalized attention, for example receiving form letter
A form letter is a letter written from a template, rather than being specially composed for a specific recipient. The most general kind of form letter consists of one or more regions of boilerplate text interspersed with one or more substitution ...
s; and the line is simply set at a point that resources allow, or where it makes business sense to stop.
Purely quantitatively, a conventional way of splitting a distribution into head and tail is to consider the head to be the first ''p'' portion of ranks, which account for of the overall population, as in the 80:20 Pareto principle, where the top 20% (head) comprises 80% of the overall population. The exact cutoff depends on the distribution ŌĆō each distribution has a single such cutoff pointŌĆöand for power, laws can be computed from the Pareto index In economics the Pareto index, named after the Italian economist and sociologist Vilfredo Pareto, is a measure of the breadth of income or wealth distribution. It is one of the parameters specifying a Pareto distribution and embodies the Pareto pr ...
.
Segments may arise naturally due to actual changes in the behavior of the distribution as rank varies. Most common is the king effect
In statistics, economics, and econophysics, the king effect is the phenomenon in which the top one or two members of a ranked set show up as clear outliers. These top one or two members are unexpectedly large because they do not conform to the s ...
, where the behavior of the top handful of items does not fit the pattern of the rest, as illustrated at the top for country populations, and above for most common words in English Wikipedia. For higher ranks, behavior may change at some point, and be well-modeled by different relations in different regions; on the whole by a piecewise function. For example, if two different power laws fit better in different regions, one can use a broken power law for the overall relation; the word frequency in English Wikipedia (above) also demonstrates this.
The YuleŌĆōSimon distribution that results from preferential attachment
A preferential attachment process is any of a class of processes in which some quantity, typically some form of wealth or credit, is distributed among a number of individuals or objects according to how much they already have, so that those who ...
(intuitively, "the rich get richer" and "success breeds success") simulates a broken power law and has been shown to "very well capture" word frequency versus rank distributions. It originated from trying to explain the population versus rank in different species. It has also been shown to fit city population versus rank better.
RankŌĆōsize rule
The rank-size rule (or law) describes the remarkable regularity in many phenomena, including the distribution of city sizes, the sizes of businesses, the sizes of particles (such as sand), the lengths of rivers, the frequencies of word usage, and wealth among individuals. All are real-world observations that followpower law
In statistics, a power law is a Function (mathematics), functional relationship between two quantities, where a Relative change and difference, relative change in one quantity results in a relative change in the other quantity proportional to the ...
s, such as Zipf's law
Zipf's law (; ) is an empirical law stating that when a list of measured values is sorted in decreasing order, the value of the -th entry is often approximately inversely proportional to .
The best known instance of Zipf's law applies to the ...
, the Yule distribution, or the Pareto distribution
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial scien ...
. If one ranks the population size of cities in a given country or in the entire world and calculates the natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
of the rank and of the city population, the resulting graph will show a linear pattern. This is the rank-size distribution.
Known exceptions to simple rankŌĆōsize distributions
While Zipf's law works well in many cases, it tends to not fit the largest cities in many countries; one type of deviation is known as theKing effect
In statistics, economics, and econophysics, the king effect is the phenomenon in which the top one or two members of a ranked set show up as clear outliers. These top one or two members are unexpectedly large because they do not conform to the s ...
. A 2002 study found that Zipf's law was rejected in 53 of 73 countries, far more than would be expected based on random chance. The study also found that variations of the Pareto exponent are better explained by political variables than by economic geography variables like proxies for economies of scale
In microeconomics, economies of scale are the cost advantages that enterprises obtain due to their scale of operation, and are typically measured by the amount of Productivity, output produced per unit of cost (production cost). A decrease in ...
or transportation costs. A 2004 study showed that Zipf's law did not work well for the five largest cities in six countries.Cuberes, David, The Rise and Decline of Cities, University of Chicago, September 29, 2004, In the richer countries, the distribution was flatter than predicted. For instance, in the United States
The United States of America (USA), also known as the United States (U.S.) or America, is a country primarily located in North America. It is a federal republic of 50 U.S. state, states and a federal capital district, Washington, D.C. The 48 ...
, although its largest city, New York City
New York, often called New York City (NYC), is the most populous city in the United States, located at the southern tip of New York State on one of the world's largest natural harbors. The city comprises five boroughs, each coextensive w ...
, has more than twice the population of second-place Los Angeles
Los Angeles, often referred to by its initials L.A., is the List of municipalities in California, most populous city in the U.S. state of California, and the commercial, Financial District, Los Angeles, financial, and Culture of Los Angeles, ...
, the two cities' metropolitan areas (also the two largest in the country) are much closer in population. In metropolitan-area population, New York City is only 1.3 times larger than Los Angeles. In other countries, the largest city would dominate much more than expected. For instance, in the Democratic Republic of the Congo
The Democratic Republic of the Congo (DRC), also known as the DR Congo, Congo-Kinshasa, or simply the Congo (the last ambiguously also referring to the neighbouring Republic of the Congo), is a country in Central Africa. By land area, it is t ...
, the capital, Kinshasa
Kinshasa (; ; ), formerly named L├®opoldville from 1881ŌĆō1966 (), is the Capital city, capital and Cities of the Democratic Republic of the Congo, largest city of the Democratic Republic of the Congo. Kinshasa is one of the world's fastest-grow ...
, is more than eight times larger than the second-largest city, Lubumbashi
Lubumbashi ( , ; former ; former ) is the second-largest Cities of the Democratic Republic of the Congo, city in the Democratic Republic of the Congo, located in the country's southeasternmost part, along the border with Zambia. The capital ...
. When considering the entire distribution of cities, including the smallest ones, the rank-size rule does not hold. Instead, the distribution is log-normal
In probability theory, a log-normal (or lognormal) distribution is a continuous probability distribution of a random variable whose logarithm is normal distribution, normally distributed. Thus, if the random variable is log-normally distributed ...
. This follows from Gibrat's law
Gibrat's law, sometimes called Gibrat's rule of proportionate growth or the law of proportionate effect, is a rule defined by Robert Gibrat (1904ŌĆō1980) in 1931 stating that the proportional rate of growth of a firm is independent of its absolut ...
of proportionate growth.
Because exceptions are so easy to find, the function of the rule for analyzing cities today is to compare the city systems in different countries. The rank-size rule is a common standard by which urban primacy is established. A distribution such as that in the United States or China does not exhibit a pattern of primacy, but countries with a dominant "primate city
A primate city is a city that is the largest in its country, province, state, or region, and disproportionately larger than any others in the urban hierarchy. A ''primate city distribution'' is a rank-size distribution that has one very large ...
" clearly vary from the rank-size rule in the opposite manner. Therefore, the rule helps to classify national (or regional) city systems according to the degree of dominance exhibited by the largest city. Countries with a primate city, for example, have typically had a colonial history that accounts for that city pattern. If a normal city distribution pattern is expected to follow the rank-size rule (i.e. if the rank-size principle correlates with central place theory), then it suggests that those countries or regions with distributions that do not follow the rule have experienced some conditions that have altered the normal distribution pattern. For example, the presence of multiple regions within large nations such as China and the United States tends to favor a pattern in which more large cities appear than would be predicted by the rule. By contrast, small countries that had been connected (e.g. colonially/economically) to much larger areas will exhibit a distribution in which the largest city is much larger than would fit the rule, compared with the other citiesŌĆöthe excessive size of the city theoretically stems from its connection with a larger system rather than the natural hierarchy that central place theory would predict within that one country or region alone.
See also
* Pareto principle *Long tail
In statistics and business, a long tail of some distributions of numbers is the portion of the distribution having many occurrences far from the "head" or central part of the distribution. The distribution could involve popularities, random n ...
References
Further reading
* * * * Douglas R. White, Laurent Tambayong, and Nata┼Īa Kej┼Šar. 2008. Oscillatory dynamics of city-size distributions in world-historical systems. ''Globalization as an Evolutionary Process: Modeling Global Change''. Ed. byGeorge Modelski
George Modelski was Professor of political science in the University of Washington. Modelski was a professor there from 1967 to 1995.
Before working at the University of Washington, Modelski was a senior research fellow at the Institute of Adva ...
, Tessaleno Devezas, and William R. Thompson. London: Routledge. The Use of Agent-Based Models in Regional Science
Ćöan agent-based simulation study that explains rankŌĆōsize distribution.
External links
* {{DEFAULTSORT:Rank-size distribution Functions related to probability distributions Geography Statistical laws