|
Joseph Sauveur
Joseph Sauveur (; 24 March 1653 – 9 July 1716) was a French mathematician and physicist. He was a professor of mathematics and in 1696 became a member of the French Academy of Sciences. Life Joseph Sauveur was born in La Flèche, the son of a provincial notary. Despite a hearing and speech impairment that kept him totally mute until he was seven, Joseph benefited from a fine education at the Jesuit College of La Flèche. At seventeen, his uncle agreed to finance his studies in philosophy and theology at Paris. Joseph, however, discovered Euclid and turned to anatomy and botany. He soon met Cordemoy, reader to the son of Louis XIV; and Cordemoy soon sang his praises to Bossuet, preceptor to the Dauphin. Despite his handicap, Joseph promptly began teaching mathematics to the Dauphine's pages and also to a number of princes, among them Eugene of Savoy. By 1680, he was something of a pet at court, where he gave anatomy courses to courtiers and calculated for them the odds in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematical model, models, and mathematics#Calculus and analysis, change. History One of the earliest known mathematicians was Thales of Miletus (); he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales's theorem. The number of known mathematicians grew when Pythagoras of Samos () established the Pythagorean school, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The first woman math ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrostatics
Hydrostatics is the branch of fluid mechanics that studies fluids at hydrostatic equilibrium and "the pressure in a fluid or exerted by a fluid on an immersed body". The word "hydrostatics" is sometimes used to refer specifically to water and other liquids, but more often it includes both gases and liquids, whether compressible or incompressible. It encompasses the study of the conditions under which fluids are at rest in stable equilibrium. It is opposed to ''fluid dynamics'', the study of fluids in motion. Hydrostatics is fundamental to ''hydraulics'', the engineering of equipment for storing, transporting and using fluids. It is also relevant to geophysics and astrophysics (for example, in understanding plate tectonics and the anomalies of the Earth's gravitational field), to meteorology, to medicine (in the context of blood pressure), and many other fields. Hydrostatics offers physical explanations for many phenomena of everyday life, such as why atmospheric pressur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Octave
In music, an octave (: eighth) or perfect octave (sometimes called the diapason) is an interval between two notes, one having twice the frequency of vibration of the other. The octave relationship is a natural phenomenon that has been referred to as the "basic miracle of music", the use of which is "common in most musical systems". The interval between the first and second harmonics of the harmonic series is an octave. In Western music notation, notes separated by an octave (or multiple octaves) have the same name and are of the same pitch class. To emphasize that it is one of the perfect intervals (including unison, perfect fourth, and perfect fifth), the octave is designated P8. Other interval qualities are also possible, though rare. The octave above or below an indicated note is sometimes abbreviated ''8a'' or ''8va'' (), ''8va bassa'' (, sometimes also ''8vb''), or simply ''8'' for the octave in the direction indicated by placing this mark above or below the staff. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Harmonics
In physics, acoustics, and telecommunications, a harmonic is a sinusoidal wave with a frequency that is a positive integer multiple of the ''fundamental frequency'' of a periodic signal. The fundamental frequency is also called the ''1st harmonic''; the other harmonics are known as ''higher harmonics''. As all harmonics are periodic at the fundamental frequency, the sum of harmonics is also periodic at that frequency. The set of harmonics forms a '' harmonic series''. The term is employed in various disciplines, including music, physics, acoustics, electronic power transmission, radio technology, and other fields. For example, if the fundamental frequency is 50 Hz, a common AC power supply frequency, the frequencies of the first three higher harmonics are 100 Hz (2nd harmonic), 150 Hz (3rd harmonic), 200 Hz (4th harmonic) and any addition of waves with these frequencies is periodic at 50 Hz. In music, harmonics are used on string instruments and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vibrating String
A vibration in a string is a wave. Resonance causes a vibrating string to produce a sound with constant frequency, i.e. constant pitch. If the length or tension of the string is correctly adjusted, the sound produced is a musical tone. Vibrating strings are the basis of string instruments such as guitars, cellos, and pianos. For an homogenous string, the motion is given by the wave equation. Wave The velocity of propagation of a wave in a string (v) is proportional to the square root of the force of tension of the string (T) and inversely proportional to the square root of the linear density (\mu) of the string: v = \sqrt. This relationship was discovered by Vincenzo Galilei in the late 1500s. Derivation Source: Let \Delta x be the length of a piece of string, m its mass, and \mu its linear density. If angles \alpha and \beta are small, then the horizontal components of tension on either side can both be approximated by a constant T, for which the net horizontal for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pitch (music)
Pitch is a perception, perceptual property that allows sounds to be ordered on a frequency-related scale (music), scale, or more commonly, pitch is the quality that makes it possible to judge sounds as "higher" and "lower" in the sense associated with musical melody, melodies. Pitch is a major auditory system, auditory attribute of musical tones, along with duration (music), duration, loudness, and timbre. Pitch may be quantified as a frequency, but pitch is not a purely objective physical property; it is a subjective Psychoacoustics, psychoacoustical attribute of sound. Historically, the study of pitch and pitch perception has been a central problem in psychoacoustics, and has been instrumental in forming and testing theories of sound representation, processing, and perception in the auditory system. Perception Pitch and frequency Pitch is an auditory sensation in which a listener assigns musical tones to relative positions on a musical scale based primarily on their percep ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals (sound), radio waves, and light. The interval of time between events is called the period. It is the reciprocal of the frequency. For example, if a heart beats at a frequency of 120 times per minute (2 hertz), its period is one half of a second. Special definitions of frequency are used in certain contexts, such as the angular frequency in rotational or cyclical properties, when the rate of angular progress is measured. Spatial frequency is defined for properties that vary or cccur repeatedly in geometry or space. The unit of measurement of frequency in the International System of Units (SI) is the hertz, having the symbol Hz. Definitions and units For cyclical phenomena such as oscillations, waves, or for examp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monochord
A monochord, also known as sonometer (see below), is an ancient musical and scientific laboratory instrument, involving one (mono-) string ( chord). The term ''monochord'' is sometimes used as the class-name for any musical stringed instrument having only one string and a stick shaped body, also known as musical bows. According to the Hornbostel–Sachs system, string bows are bar zithers (311.1) while monochords are traditionally board zithers (314). The "harmonical canon", or monochord is, at its least, "merely a string having a board under it of exactly the same length, upon which may be delineated the points at which the string must be stopped to give certain notes," allowing comparison. A string is fixed at both ends and stretched over a sound box. One or more movable bridges are then manipulated to demonstrate mathematical relationships among the frequencies produced. "With its single string, movable bridge and graduated rule, the monochord (''kanōn'' reek: law str ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics technology may be called an Acoustical engineering, acoustical engineer. The application of acoustics is present in almost all aspects of modern society with the most obvious being the audio and noise control industries. Hearing (sense), Hearing is one of the most crucial means of survival in the animal world and speech is one of the most distinctive characteristics of human development and culture. Accordingly, the science of acoustics spreads across many facets of human society—music, medicine, architecture, industrial production, warfare and more. Likewise, animal species such as songbirds and frogs use sound and hearing as a key element of mating rituals or for marking territories. Art, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Collège De France
The (), formerly known as the or as the ''Collège impérial'' founded in 1530 by François I, is a higher education and research establishment () in France. It is located in Paris near La Sorbonne. The has been considered to be France's most prestigious research establishment. It is an associate member of PSL University. Research and teaching are closely linked at the , whose ambition is to teach "the knowledge that is being built up in all fields of literature, science and the arts". Overview As of 2021, 21 Nobel Prize winners and 9 Fields Medalists have been affiliated with the Collège. It does not grant degrees. Each professor is required to give lectures where attendance is free and open to anyone. Professors, about 50 in number, are chosen by the professors themselves, from a variety of disciplines, in both science and the humanities. The motto of the Collège is ''Docet Omnia'', Latin for "It teaches everything"; its goal is to "teach science in the making" and ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Étienne Loulié
Étienne Loulié (; 165416 July 1702) was a musician, pedagogue, and musical theorist. Life Born into a family of Parisian sword-finishers, Loulié learned both musical practice and musical theory as a choir boy at the Sainte-Chapelle of Paris, under the learned ''maître de musique'' René Ouvrard. In 1673 Loulié left the Chapel and entered the service of Marie de Lorraine, duchesse de Guise, as an instrumentalist (harpsichord, and organ, viol, recorder and perhaps transverse flute as well), performing chiefly in her household ensemble. From 1673 to late 1687, he therefore performed many of the compositions of Marc-Antoine Charpentier, the Guises' household composer. During the late 1680s, Loulié became involved in musical pedagogy and wrote a series of coordinated method books for music teachers. He is credited with introducing the six-fold system of meter classification still taught today. During these same years, he formed a lifelong friendship with Sébastien de Brossard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
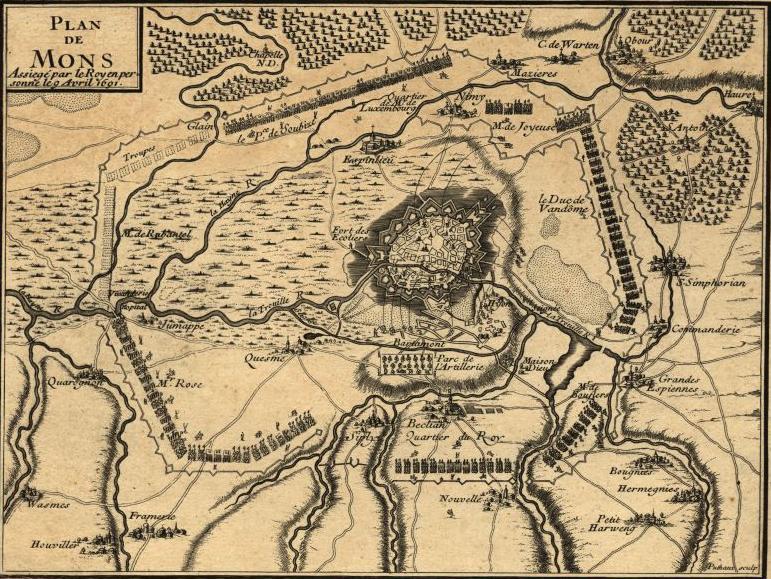
Siege Of Mons (1691)
The siege of Mons, 15 March – 10 April 1691, was a major operation fought during the Nine Years' War, and was the main French objective for the 1691 campaign in the Spanish Netherlands. The city was besieged and captured before the normal commencement of the campaigning season with minimal losses. The outcome was not in doubt, but in a conflict dominated by siege warfare, neither the French army of King Louis XIV, nor the forces of the Grand Alliance under King William III, could bring about a decisive battle. After the siege the duc de Boufflers bombarded the neutral city of Liège, whilst the duc de Luxembourg captured Halle, and scored a minor victory against the Prince of Waldeck at the Battle of Leuze in September. Strategically, however, little had changed in the war, and both combatants returned to winter quarters at the end of the campaigning season. Background French forces had secured considerable success in 1690. In July Luxembourg fought and won his tactical ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |