|
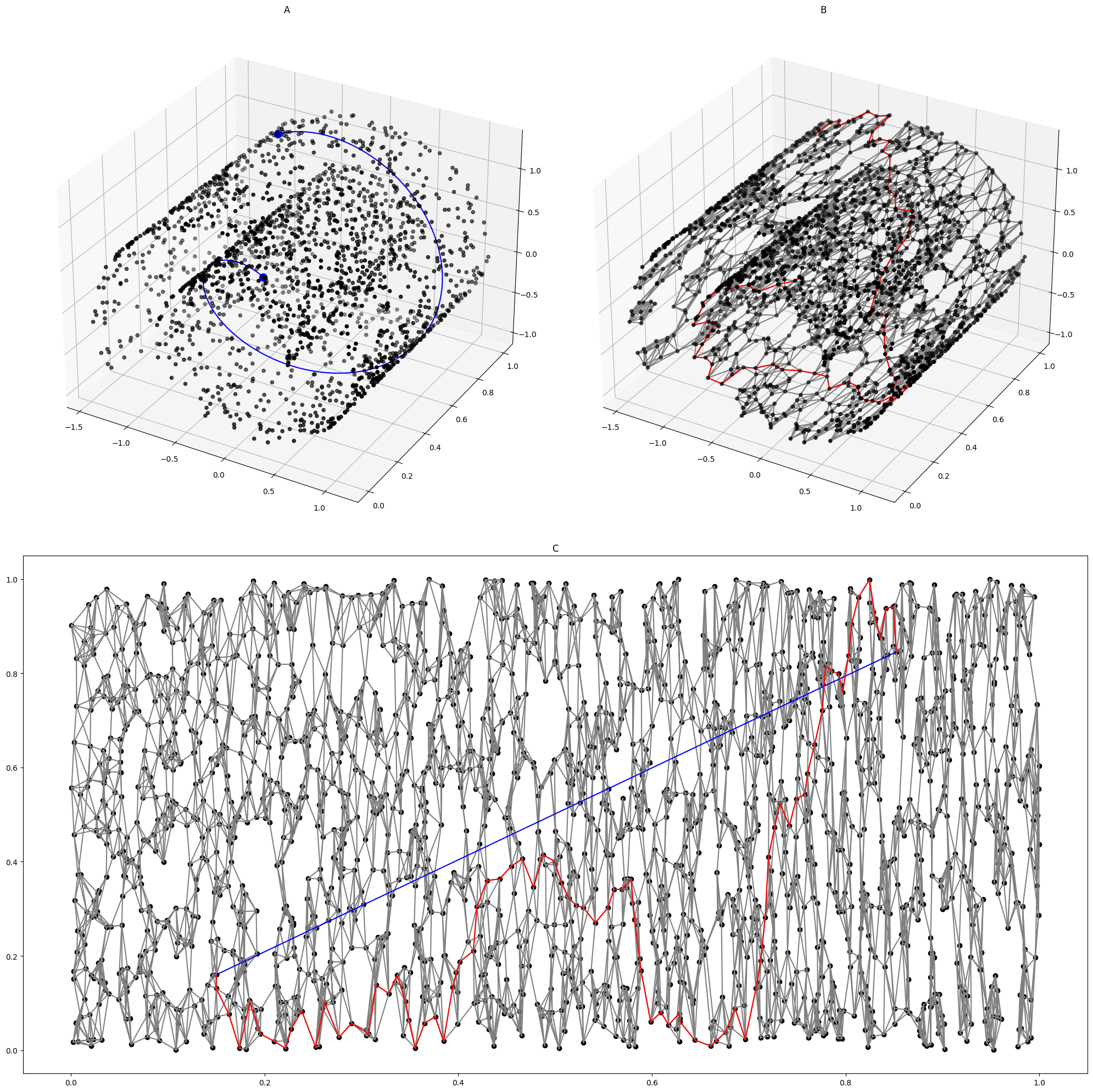
Isomap On Swiss Roll
Isomap is a nonlinear dimensionality reduction method. It is one of several widely used low-dimensional embedding methods. Isomap is used for computing a quasi-isometric, low-dimensional embedding of a set of high-dimensional data points. The algorithm provides a simple method for estimating the intrinsic geometry of a data manifold based on a rough estimate of each data point’s neighbors on the manifold. Isomap is highly efficient and generally applicable to a broad range of data sources and dimensionalities. Introduction Isomap is one representative of isometric mapping methods, and extends metric multidimensional scaling (MDS) by incorporating the geodesic distances imposed by a weighted graph. To be specific, the classical scaling of metric MDS performs low-dimensional embedding based on the pairwise distance between data points, which is generally measured using straight-line Euclidean distance. Isomap is distinguished by its use of the geodesic distance induced by a n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multidimensional Scaling
Multidimensional scaling (MDS) is a means of visualizing the level of similarity of individual cases of a data set. MDS is used to translate distances between each pair of n objects in a set into a configuration of n points mapped into an abstract Cartesian space. More technically, MDS refers to a set of related ordination techniques used in information visualization, in particular to display the information contained in a distance matrix. It is a form of non-linear dimensionality reduction. Given a distance matrix with the distances between each pair of objects in a set, and a chosen number of dimensions, ''N'', an MDS algorithm places each object into ''N''-dimensional space (a lower-dimensional representation) such that the between-object distances are preserved as well as possible. For ''N'' = 1, 2, and 3, the resulting points can be visualized on a scatter plot. Core theoretical contributions to MDS were made by James O. Ramsay of McGill University, who is also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel PCA
In the field of multivariate statistics, kernel principal component analysis (kernel PCA) is an extension of principal component analysis (PCA) using techniques of kernel methods. Using a kernel, the originally linear operations of PCA are performed in a reproducing kernel Hilbert space. Background: Linear PCA Recall that conventional PCA operates on zero-centered data; that is, :\frac\sum_^N \mathbf_i = \mathbf, where \mathbf_i is one of the N multivariate observations. It operates by diagonalizing the covariance matrix, :C=\frac\sum_^N \mathbf_i\mathbf_i^\top in other words, it gives an eigendecomposition of a matrix, eigendecomposition of the covariance matrix: :\lambda \mathbf=C\mathbf which can be rewritten as :\lambda \mathbf_i^\top \mathbf=\mathbf_i^\top C\mathbf \quad \textrm~i=1,\ldots,N. (See also: Covariance matrix#Covariance matrix as a linear operator, Covariance matrix as a linear operator) Introduction of the Kernel to PCA To understand the utility of kernel PCA, pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mercer's Theorem
In mathematics, specifically functional analysis, Mercer's theorem is a representation of a symmetric positive-definite function on a square as a sum of a convergent sequence of product functions. This theorem, presented in , is one of the most notable results of the work of James Mercer (1883–1932). It is an important theoretical tool in the theory of integral equations; it is used in the Hilbert space theory of stochastic processes, for example the Karhunen–Loève theorem; and it is also used in the reproducing kernel Hilbert space theory where it characterizes a symmetric positive-definite kernel as a reproducing kernel. Introduction To explain Mercer's theorem, we first consider an important special case; see below for a more general formulation. A ''kernel'', in this context, is a symmetric continuous function : K: ,b\times ,b\rightarrow \mathbb where K(x,y) = K(y,x) for all x,y \in ,b/math>. ''K'' is said to be a positive-definite kernel if and only if ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive Semidefinite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Method
In machine learning, kernel machines are a class of algorithms for pattern analysis, whose best known member is the support-vector machine (SVM). These methods involve using linear classifiers to solve nonlinear problems. The general task of pattern analysis is to find and study general types of relations (for example clusters, rankings, principal components, correlations, classifications) in datasets. For many algorithms that solve these tasks, the data in raw representation have to be explicitly transformed into feature vector representations via a user-specified ''feature map'': in contrast, kernel methods require only a user-specified ''kernel'', i.e., a similarity function over all pairs of data points computed using inner products. The feature map in kernel machines is infinite dimensional but only requires a finite dimensional matrix from user-input according to the representer theorem. Kernel machines are slow to compute for datasets larger than a couple of thousand exam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel PCA
In the field of multivariate statistics, kernel principal component analysis (kernel PCA) is an extension of principal component analysis (PCA) using techniques of kernel methods. Using a kernel, the originally linear operations of PCA are performed in a reproducing kernel Hilbert space. Background: Linear PCA Recall that conventional PCA operates on zero-centered data; that is, :\frac\sum_^N \mathbf_i = \mathbf, where \mathbf_i is one of the N multivariate observations. It operates by diagonalizing the covariance matrix, :C=\frac\sum_^N \mathbf_i\mathbf_i^\top in other words, it gives an eigendecomposition of a matrix, eigendecomposition of the covariance matrix: :\lambda \mathbf=C\mathbf which can be rewritten as :\lambda \mathbf_i^\top \mathbf=\mathbf_i^\top C\mathbf \quad \textrm~i=1,\ldots,N. (See also: Covariance matrix#Covariance matrix as a linear operator, Covariance matrix as a linear operator) Introduction of the Kernel to PCA To understand the utility of kernel PCA, pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Principal Component Analysis
Principal component analysis (PCA) is a linear dimensionality reduction technique with applications in exploratory data analysis, visualization and data preprocessing. The data is linearly transformed onto a new coordinate system such that the directions (principal components) capturing the largest variation in the data can be easily identified. The principal components of a collection of points in a real coordinate space are a sequence of p unit vectors, where the i-th vector is the direction of a line that best fits the data while being orthogonal to the first i-1 vectors. Here, a best-fitting line is defined as one that minimizes the average squared perpendicular distance from the points to the line. These directions (i.e., principal components) constitute an orthonormal basis in which different individual dimensions of the data are linearly uncorrelated. Many studies use the first two principal components in order to plot the data in two dimensions and to visually identi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel Transport
In differential geometry, parallel transport (or parallel translation) is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection (a covariant derivative or connection on the tangent bundle), then this connection allows one to transport vectors of the manifold along curves so that they stay '' parallel'' with respect to the connection. The parallel transport for a connection thus supplies a way of, in some sense, moving the local geometry of a manifold along a curve: that is, of ''connecting'' the geometries of nearby points. There may be many notions of parallel transport available, but a specification of one way of connecting up the geometries of points on a curve is tantamount to providing a ''connection''. In fact, the usual notion of connection is the infinitesimal analog of parallel transport. Or, ''vice versa'', parallel transport is the local realization of a connection. As parallel transport suppl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Floyd–Warshall Algorithm
In computer science, the Floyd–Warshall algorithm (also known as Floyd's algorithm, the Roy–Warshall algorithm, the Roy–Floyd algorithm, or the WFI algorithm) is an algorithm for finding shortest paths in a directed weighted graph with positive or negative edge weights (but with no negative cycles). See in particular Section 26.2, "The Floyd–Warshall algorithm", pp. 558–565 and Section 26.4, "A general framework for solving path problems in directed graphs", pp. 570–576. A single execution of the algorithm will find the lengths (summed weights) of shortest paths between all pairs of vertices. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm. Versions of the algorithm can also be used for finding the transitive closure of a relation R, or (in connection with the Schulze voting system) widest paths between all pairs of vertices in a weighted graph. History and nam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Dimensionality Reduction
Nonlinear dimensionality reduction, also known as manifold learning, is any of various related techniques that aim to project high-dimensional data, potentially existing across non-linear manifolds which cannot be adequately captured by linear decomposition methods, onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping (either from the high-dimensional space to the low-dimensional embedding or vice versa) itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis. Applications of NLDR High dimensional data can be hard for machines to work with, requiring significant time and space for analysis. It also presents a challenge for humans, since it's hard to visualize or understand data in more than three dimensions. Reducing the dimensionality of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |