|
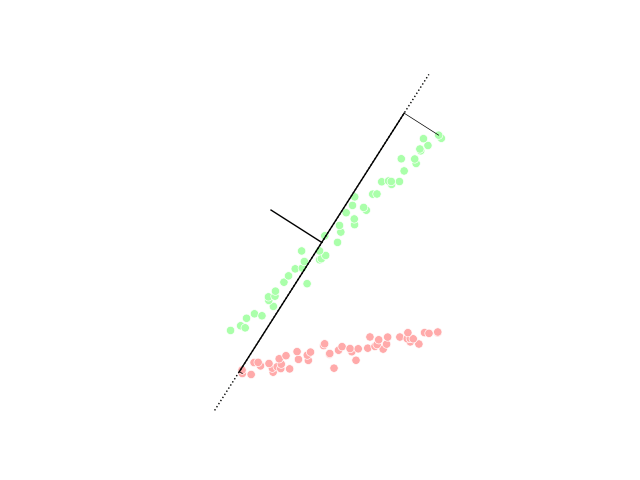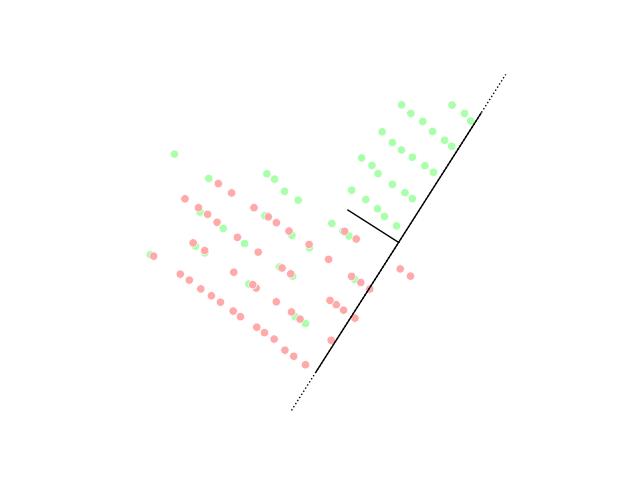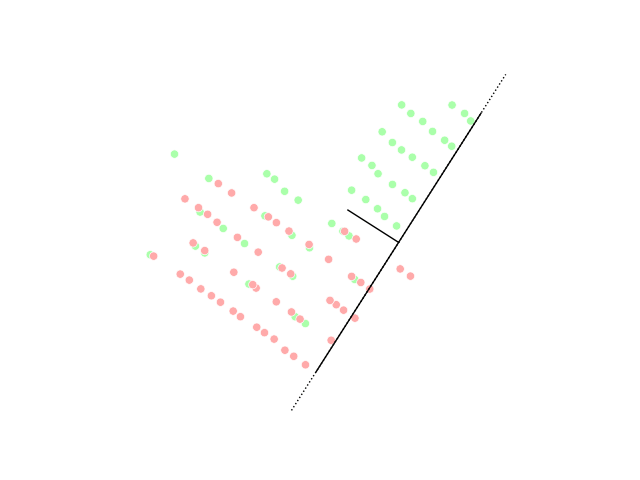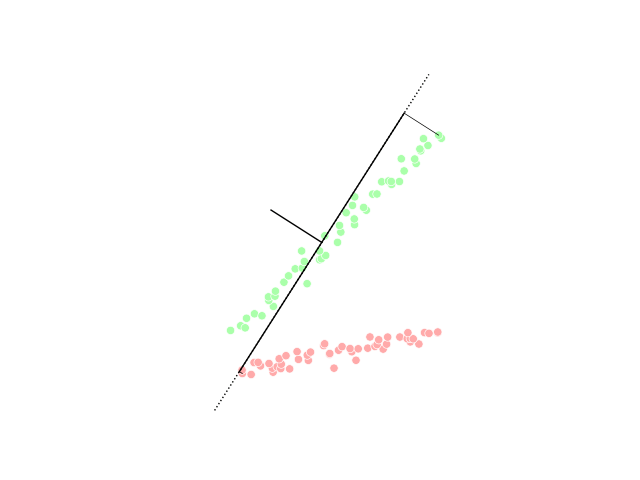
Kernel PCA
In the field of multivariate statistics, kernel principal component analysis (kernel PCA) is an extension of principal component analysis (PCA) using techniques of kernel methods. Using a kernel, the originally linear operations of PCA are performed in a reproducing kernel Hilbert space. Background: Linear PCA Recall that conventional PCA operates on zero-centered data; that is, :\frac\sum_^N \mathbf_i = \mathbf, where \mathbf_i is one of the N multivariate observations. It operates by diagonalizing the covariance matrix, :C=\frac\sum_^N \mathbf_i\mathbf_i^\top in other words, it gives an eigendecomposition of a matrix, eigendecomposition of the covariance matrix: :\lambda \mathbf=C\mathbf which can be rewritten as :\lambda \mathbf_i^\top \mathbf=\mathbf_i^\top C\mathbf \quad \textrm~i=1,\ldots,N. (See also: Covariance matrix#Covariance matrix as a linear operator, Covariance matrix as a linear operator) Introduction of the Kernel to PCA To understand the utility of kernel PCA, pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Statistics
Multivariate statistics is a subdivision of statistics encompassing the simultaneous observation and analysis of more than one outcome variable, i.e., '' multivariate random variables''. Multivariate statistics concerns understanding the different aims and background of each of the different forms of multivariate analysis, and how they relate to each other. The practical application of multivariate statistics to a particular problem may involve several types of univariate and multivariate analyses in order to understand the relationships between variables and their relevance to the problem being studied. In addition, multivariate statistics is concerned with multivariate probability distributions, in terms of both :*how these can be used to represent the distributions of observed data; :*how they can be used as part of statistical inference, particularly where several different quantities are of interest to the same analysis. Certain types of problems involving multivariate da ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Centering Matrix
In mathematics and multivariate statistics, the centering matrixJohn I. Marden, ''Analyzing and Modeling Rank Data'', Chapman & Hall, 1995, , page 59. is a symmetric and idempotent matrix, which when multiplied with a vector has the same effect as subtracting the mean of the components of the vector from every component of that vector. Definition The centering matrix of size ''n'' is defined as the ''n''-by-''n'' matrix :C_n = I_n - \tfracJ_n where I_n\, is the identity matrix of size ''n'' and J_n is an ''n''-by-''n'' matrix of all 1's. For example :C_1 = \begin 0 \end , :C_2= \left \begin 1 & 0 \\ 0 & 1 \end \right- \frac\left \begin 1 & 1 \\ 1 & 1 \end \right = \left \begin \frac & -\frac \\ -\frac & \frac \end \right , :C_3 = \left \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end \right- \frac\left \begin 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end \right = \left \begin \frac & -\frac & -\frac \\ -\frac & \frac & -\frac \\ -\frac & -\frac & \frac \end \right ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Machine Learning Algorithms
The following outline is provided as an overview of, and topical guide to, machine learning: Machine learning (ML) is a subfield of artificial intelligence within computer science that evolved from the study of pattern recognition and computational learning theory.http://www.britannica.com/EBchecked/topic/1116194/machine-learning In 1959, Arthur Samuel defined machine learning as a "field of study that gives computers the ability to learn without being explicitly programmed". ML involves the study and construction of algorithms that can learn from and make predictions on data. These algorithms operate by building a model from a training set of example observations to make data-driven predictions or decisions expressed as outputs, rather than following strictly static program instructions. How can machine learning be categorized? * An academic discipline * A branch of science ** An applied science *** A subfield of computer science **** A branch of artificial intelligenc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
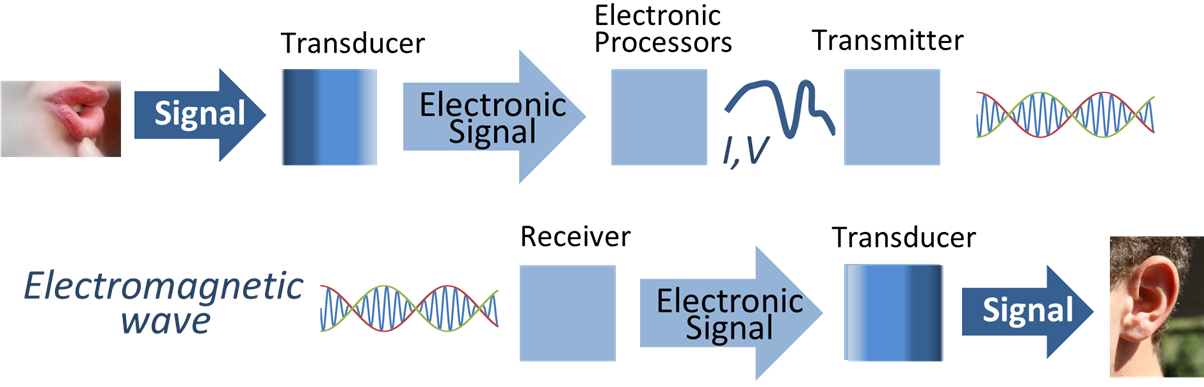
Signal Processing
Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomography, seismic signals, Altimeter, altimetry processing, and scientific measurements. Signal processing techniques are used to optimize transmissions, Data storage, digital storage efficiency, correcting distorted signals, improve subjective video quality, and to detect or pinpoint components of interest in a measured signal. History According to Alan V. Oppenheim and Ronald W. Schafer, the principles of signal processing can be found in the classical numerical analysis techniques of the 17th century. They further state that the digital refinement of these techniques can be found in the digital control systems of the 1940s and 1950s. In 1948, Claude Shannon wrote the influential paper "A Mathematical Theory of Communication" which was publis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension Reduction
Dimensionality reduction, or dimension reduction, is the transformation of data from a high-dimensional space into a low-dimensional space so that the low-dimensional representation retains some meaningful properties of the original data, ideally close to its intrinsic dimension. Working in high-dimensional spaces can be undesirable for many reasons; raw data are often sparse as a consequence of the curse of dimensionality, and analyzing the data is usually computationally intractable. Dimensionality reduction is common in fields that deal with large numbers of observations and/or large numbers of variables, such as signal processing, speech recognition, neuroinformatics, and bioinformatics. Methods are commonly divided into linear and nonlinear approaches. Linear approaches can be further divided into feature selection and feature extraction. Dimensionality reduction can be used for noise reduction, data visualization, cluster analysis, or as an intermediate step to facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spectral Clustering
In multivariate statistics, spectral clustering techniques make use of the spectrum (eigenvalues) of the similarity matrix of the data to perform dimensionality reduction before clustering in fewer dimensions. The similarity matrix is provided as an input and consists of a quantitative assessment of the relative similarity of each pair of points in the dataset. In application to image segmentation, spectral clustering is known as segmentation-based object categorization. Definitions Given an enumerated set of data points, the similarity matrix may be defined as a symmetric matrix A, where A_\geq 0 represents a measure of the similarity between data points with indices i and j. The general approach to spectral clustering is to use a standard clustering method (there are many such methods, ''k''-means is discussed below) on relevant eigenvectors of a Laplacian matrix of A. There are many different ways to define a Laplacian which have different mathematical interpretatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Dimensionality Reduction
Nonlinear dimensionality reduction, also known as manifold learning, is any of various related techniques that aim to project high-dimensional data, potentially existing across non-linear manifolds which cannot be adequately captured by linear decomposition methods, onto lower-dimensional latent manifolds, with the goal of either visualizing the data in the low-dimensional space, or learning the mapping (either from the high-dimensional space to the low-dimensional embedding or vice versa) itself. The techniques described below can be understood as generalizations of linear decomposition methods used for dimensionality reduction, such as singular value decomposition and principal component analysis. Applications of NLDR High dimensional data can be hard for machines to work with, requiring significant time and space for analysis. It also presents a challenge for humans, since it's hard to visualize or understand data in more than three dimensions. Reducing the dimensionality of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cluster Analysis
Cluster analysis or clustering is the data analyzing technique in which task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more Similarity measure, similar (in some specific sense defined by the analyst) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistics, statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis refers to a family of algorithms and tasks rather than one specific algorithm. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small Distance function, distances between cluster members, dense areas of the data space, intervals or pa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Pca Output Gaussian
Kernel may refer to: Computing * Kernel (operating system), the central component of most operating systems * Kernel (image processing), a matrix used for image convolution * Compute kernel, in GPGPU programming * Kernel method, in machine learning * Kernelization, a technique for designing efficient algorithms ** Kernel, a routine that is executed in a vectorized loop, for example in general-purpose computing on graphics processing units *KERNAL, the Commodore operating system Mathematics Objects * Kernel (algebra), a general concept that includes: ** Kernel (linear algebra) or null space, a set of vectors mapped to the zero vector ** Kernel (category theory), a generalization of the kernel of a homomorphism ** Kernel (set theory), an equivalence relation: partition by image under a function ** Difference kernel, a binary equalizer: the kernel of the difference of two functions Functions * Kernel (geometry), the set of points within a polygon from which the whole polygon boun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
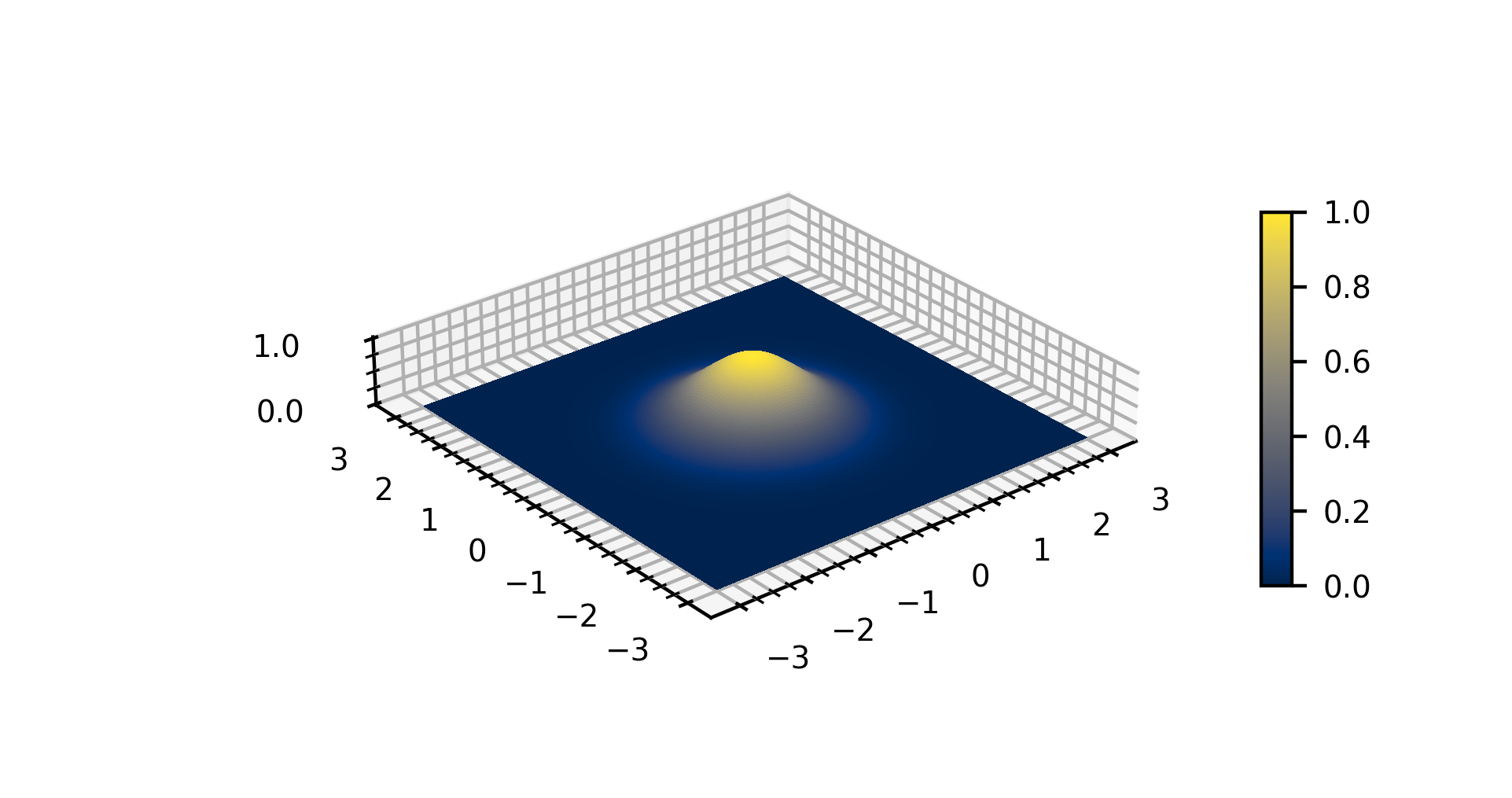
Gaussian Kernel
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real constants , and non-zero . It is named after the mathematician Carl Friedrich Gauss. The graph of a Gaussian is a characteristic symmetric " bell curve" shape. The parameter is the height of the curve's peak, is the position of the center of the peak, and (the standard deviation, sometimes called the Gaussian RMS width) controls the width of the "bell". Gaussian functions are often used to represent the probability density function of a normally distributed random variable with expected value and variance . In this case, the Gaussian is of the form g(x) = \frac \exp\left( -\frac \frac \right). Gaussian functions are widely used in statistics to describe the normal distributions, in signal processing to define Gaussian filters, in image processing where two-dimens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kernel Pca Output
Kernel may refer to: Computing * Kernel (operating system), the central component of most operating systems * Kernel (image processing), a matrix used for image convolution * Compute kernel, in GPGPU programming * Kernel method, in machine learning * Kernelization, a technique for designing efficient algorithms ** Kernel, a routine that is executed in a vectorized loop, for example in general-purpose computing on graphics processing units *KERNAL, the Commodore operating system Mathematics Objects * Kernel (algebra), a general concept that includes: ** Kernel (linear algebra) or null space, a set of vectors mapped to the zero vector ** Kernel (category theory), a generalization of the kernel of a homomorphism ** Kernel (set theory), an equivalence relation: partition by image under a function ** Difference kernel, a binary equalizer: the kernel of the difference of two functions Functions * Kernel (geometry), the set of points within a polygon from which the whole polygon boun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |