|
Iso-damping
Iso-damping is a desirable system property referring to a state where the open-loop phase Bode plot is flat—i.e., the phase derivative with respect to the frequency is zero, at a given frequency called the "tangent frequency", _c. At the "tangent frequency" the Nyquist curve of the open-loop system tangentially touches the sensitivity circle and the phase Bode is locally flat which implies that the system will be more robust to gain variations. For systems that exhibit iso-damping property, the overshoots of the closed-loop step responses will remain almost constant for different values of the controller gain. This will ensure that the closed-loop system is robust to gain variations. The iso-damping property can be expressed as \frac_ = 0, or equivalently: : \angle \frac_ = \angle G(s)_, where \omega_c is the tangent frequency and G(s) is the open-loop system transfer function. Bode's ideal transfer function In the middle of the 20th century, Bode proposed the first idea in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Robust Control
In control theory, robust control is an approach to controller design that explicitly deals with uncertainty. Robust control methods are designed to function properly provided that uncertain parameters or disturbances are found within some (typically compact) set. Robust methods aim to achieve robust performance and/or stability in the presence of bounded modelling errors. The early methods of Bode and others were fairly robust; the state-space methods invented in the 1960s and 1970s were sometimes found to lack robustness, prompting research to improve them. This was the start of the theory of robust control, which took shape in the 1980s and 1990s and is still active today. In contrast with an adaptive control policy, a robust control policy is static, rather than adapting to measurements of variations, the controller is designed to work assuming that certain variables will be unknown but bounded. (Section 1.5) In German; an English version is also available Criteria for robustn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nyquist Plot
In control theory and stability theory, the Nyquist stability criterion or Strecker–Nyquist stability criterion, independently discovered by the German electrical engineer at Siemens in 1930 and the Swedish-American electrical engineer Harry Nyquist at Bell Telephone Laboratories in 1932, is a graphical technique for determining the stability of a dynamical system. Because it only looks at the Nyquist plot of the open loop systems, it can be applied without explicitly computing the poles and zeros of either the closed-loop or open-loop system (although the number of each type of right-half-plane singularities must be known). As a result, it can be applied to systems defined by non-rational functions, such as systems with delays. In contrast to Bode plots, it can handle transfer functions with right half-plane singularities. In addition, there is a natural generalization to more complex systems with multiple inputs and multiple outputs, such as control systems for airplane ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
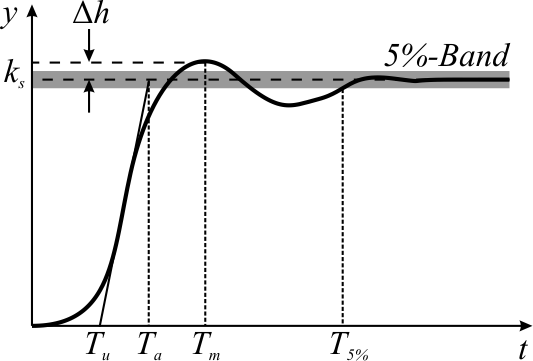
Overshoot (signal)
In signal processing, control theory, electronics, and mathematics, overshoot is the occurrence of a signal or function exceeding its target. Undershoot is the same phenomenon in the opposite direction. It arises especially in the step response of bandlimited systems such as low-pass filters. It is often followed by ringing, and at times conflated with the latter. Definition Maximum overshoot is defined in Katsuhiko Ogata's ''Discrete-time control systems'' as "the maximum peak value of the response curve measured from the desired response of the system." Control theory In control theory, overshoot refers to an output exceeding its final, steady-state value. For a step input, the ''percentage overshoot'' (PO) is the maximum value minus the step value divided by the step value. In the case of the unit step, the ''overshoot'' is just the maximum value of the step response minus one. Also see the definition of ''overshoot'' in an electronics context. For second-order sys ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
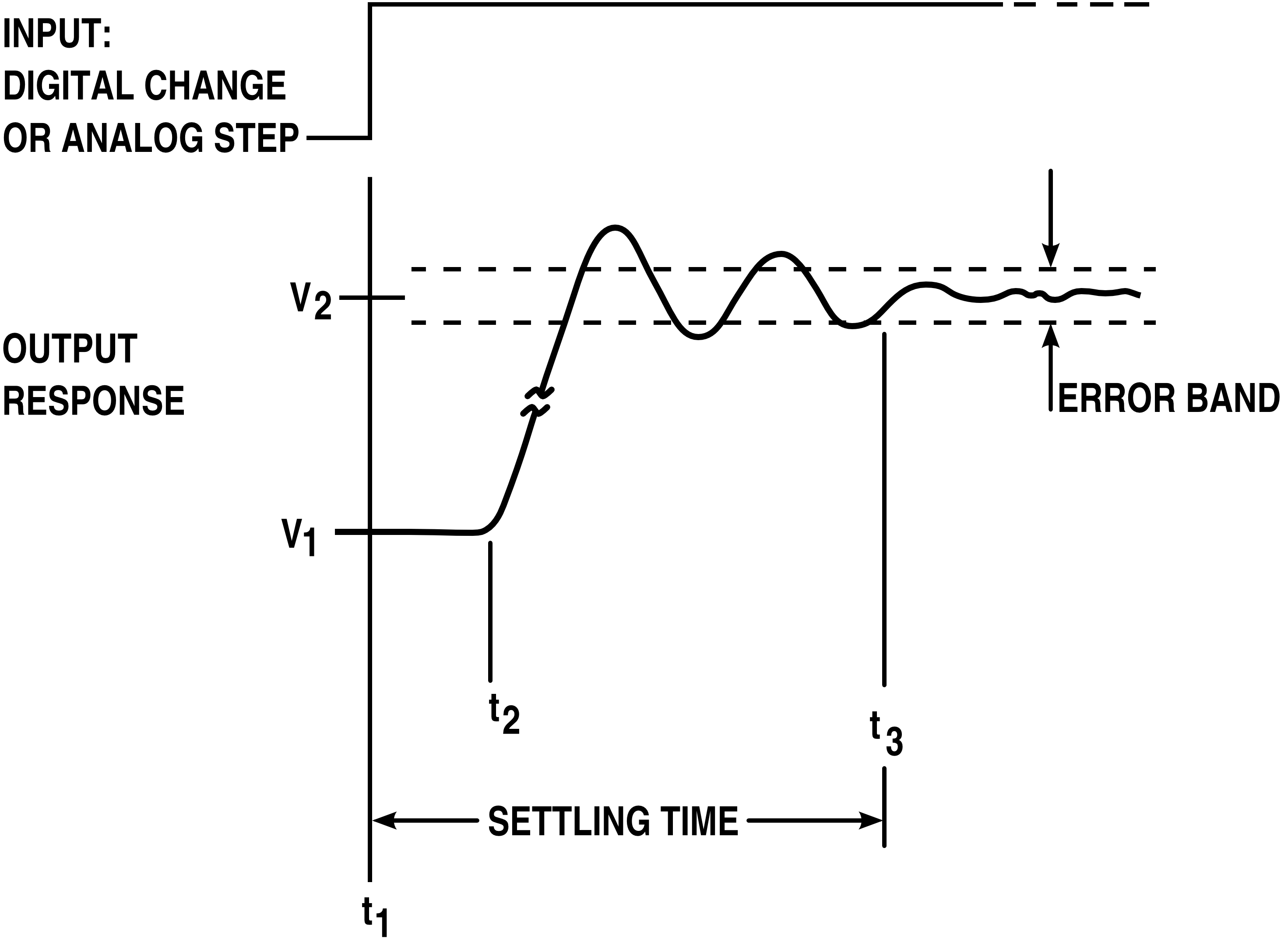
Step Response
The step response of a system in a given initial state consists of the time evolution of its outputs when its control inputs are Heaviside step functions. In electronic engineering and control theory, step response is the time behaviour of the outputs of a general system when its inputs change from zero to one in a very short time. The concept can be extended to the abstract mathematical notion of a dynamical system using an evolution parameter. From a practical standpoint, knowing how the system responds to a sudden input is important because large and possibly fast deviations from the long term steady state may have extreme effects on the component itself and on other portions of the overall system dependent on this component. In addition, the overall system cannot act until the component's output settles down to some vicinity of its final state, delaying the overall system response. Formally, knowing the step response of a dynamical system gives information on the stability of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hendrik Wade Bode
Hendrik Wade Bode ( ; ;Van Valkenburg, M. E. University of Illinois at Urbana-Champaign, "In memoriam: Hendrik W. Bode (1905-1982)", IEEE Transactions on Automatic Control, Vol. AC-29, No 3., March 1984, pp. 193–194. Quote: "Something should be said about his name. To his colleagues at Bell Laboratories and the generations of engineers that have followed, the pronunciation is boh-dee. The Bode family preferred that the original Dutch be used as boh-dah." December 24, 1905 – June 21, 1982) was an American engineer, researcher, inventor, author and scientist, of Dutch ancestry. As a pioneer of modern control theory and electronic telecommunications he revolutionized both the content and methodology of his chosen fields of research. His synergy with Claude Shannon, the father of information theory, laid the foundations for the technological convergence of the information age. He made important contributions to the design, guidance and control of anti-aircraft systems during World ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional-order Control
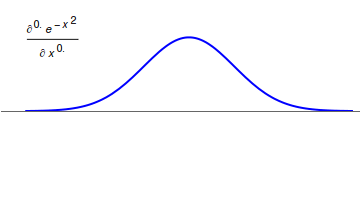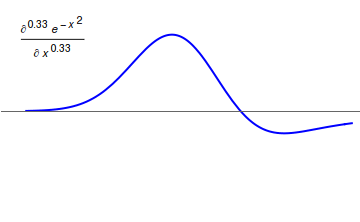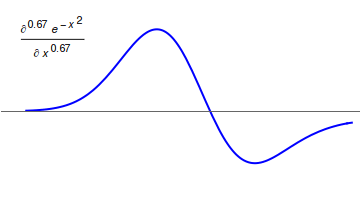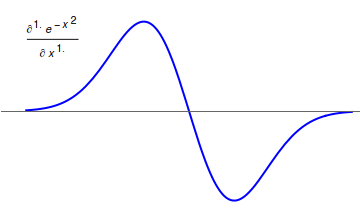
Fractional-order control (FOC) is a field of control theory that uses the fractional-order integrator as part of the control system design toolkit. The use of fractional calculus (FC) can improve and generalize well-established control methods and strategies. The fundamental advantage of FOC is that the fractional-order integrator weights history using a function that decays with a power-law tail. The effect is that the effects of all time are computed for each iteration of the control algorithm. This creates a 'distribution of time constants,' the upshot of which is there is no particular time constant, or resonance frequency, for the system. In fact, the fractional integral operator \frac is different from any integer-order rational transfer function (s), in the sense that it is a non-local operator that possesses an infinite memory and takes into account the whole history of its input signal. Fractional-order control shows promise in many controlled environments that suff ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Calculus
Fractional calculus is a branch of mathematical analysis that studies the several different possibilities of defining real number powers or complex number powers of the differentiation operator D :D f(x) = \frac f(x)\,, and of the integration operator J The symbol J is commonly used instead of the intuitive I in order to avoid confusion with other concepts identified by similar I–like glyphs, such as identities. :J f(x) = \int_0^x f(s) \,ds\,, and developing a calculus for such operators generalizing the classical one. In this context, the term ''powers'' refers to iterative application of a linear operator D to a function f, that is, repeatedly composing D with itself, as in D^n(f) = (\underbrace_n)(f) = \underbrace_n (f)\cdots))). For example, one may ask for a meaningful interpretation of :\sqrt = D^\frac12 as an analogue of the functional square root for the differentiation operator, that is, an expression for some linear operator that, when applied ''twice'' to an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Process Control
An industrial process control in continuous production processes is a discipline that uses industrial control systems to achieve a production level of consistency, economy and safety which could not be achieved purely by human manual control. It is implemented widely in industries such as automotive, mining, dredging, oil refining, pulp and paper manufacturing, chemical processing and power generating plants. There is a wide range of size, type and complexity, but it enables a small number of operators to manage complex processes to a high degree of consistency. The development of large industrial process control systems was instrumental in enabling the design of large high volume and complex processes, which could not be otherwise economically or safely operated. The applications can range from controlling the temperature and level of a single process vessel, to a complete chemical processing plant with several thousand control loops. History Early process control breakthr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Dynamics (journal)
''Nonlinear Dynamics, An International Journal of Nonlinear Dynamics and Chaos in Engineering Systems'' is a monthly peer-reviewed scientific journal covering all nonlinear dynamic phenomena associated with mechanical, structural, civil, aeronautical, ocean, electrical, and control systems. It is published by Springer Nature and the editor-in-chief of the journal is Walter Lacarbonara (Sapienza University of Rome). It should not be confused with the similarly named Russian journal ''Nelineinaya Dinamika'' (or the ''Russian Journal of Nonlinear Dynamics''). Abstracting and indexing The journal is abstracted and indexed in: According to the ''Journal Citation Reports'', the journal has a 2021 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a scientometric index calculated by Clarivate that reflects the yearly mean number of citations of articles published in the last two years in a given journal, as ... of 5.741. References ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phase Margin
Phase or phases may refer to: Science *State of matter, or phase, one of the distinct forms in which matter can exist *Phase (matter), a region of space throughout which all physical properties are essentially uniform *Phase space, a mathematical space in which each possible state of a physical system is represented by a point — this equilibrium point is also referred to as a "microscopic state" **Phase space formulation, a formulation of quantum mechanics in phase space *Phase (waves), the position of a point in time (an instant) on a waveform cycle **Instantaneous phase, generalization for both cyclic and non-cyclic phenomena * AC phase, the phase offset between alternating current electric power in multiple conducting wires **Single-phase electric power, distribution of AC electric power in a system where the voltages of the supply vary in unison **Three-phase electric power, a common method of AC electric power generation, transmission, and distribution *Phase problem, the l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |