signal processing Signal processing is an electrical engineering subfield that focuses on analyzing, modifying and synthesizing ''signals'', such as audio signal processing, sound, image processing, images, Scalar potential, potential fields, Seismic tomograph ...

control theory Control theory is a field of control engineering and applied mathematics that deals with the control system, control of dynamical systems in engineered processes and machines. The objective is to develop a model or algorithm governing the applic ...

electronics Electronics is a scientific and engineering discipline that studies and applies the principles of physics to design, create, and operate devices that manipulate electrons and other Electric charge, electrically charged particles. It is a subfield ...

, and

mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...

, overshoot is the occurrence of a signal or function exceeding its target. Undershoot is the same phenomenon in the opposite direction. It arises especially in the step response of

bandlimited Bandlimiting is the process of reducing a signal’s energy outside a specific frequency range, keeping only the desired part of the signal’s spectrum. This technique is crucial in signal processing and communications to ensure signals stay cl ...

systems such as

low-pass filter A low-pass filter is a filter that passes signals with a frequency lower than a selected cutoff frequency and attenuates signals with frequencies higher than the cutoff frequency. The exact frequency response of the filter depends on the filt ...

s. It is often followed by ringing, and at times conflated with the latter.

Definition

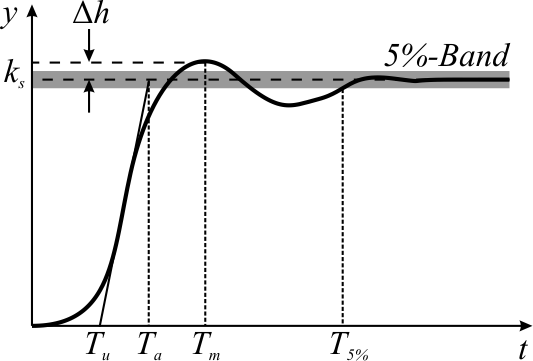
Maximum overshoot is defined in Katsuhiko Ogata's ''Discrete-time control systems'' as "the maximum peak value of the response curve measured from the desired response of the system."

Control theory

, overshoot refers to an output exceeding its final, steady-state value. For a step input, the ''percentage overshoot'' (PO) is the maximum value minus the step value divided by the step value. In the case of the unit step, the ''overshoot'' is just the maximum value of the step response minus one. Also see the definition of ''overshoot'' in an electronics context. For second-order systems, the percentage overshoot is a function of the

damping ratio In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include ...

''ζ'' and is given by Modern Control Engineering (3rd Edition), Katsuhiko Ogata, page 153. :

\mathrm = 100 \exp \left (\frac\right )

The damping ratio can also be found by :

\zeta = \frac

Electronics

In electronics, ''overshoot'' refers to the transitory values of any parameter that exceeds its final (steady state) value during its transition from one value to another. An important application of the term is to the output signal of an amplifier. ''Usage'': Overshoot occurs when the transitory values exceed final value. When they are lower than the final value, the phenomenon is called ''"undershoot"''. A circuit is designed to minimize

rise time In electronics, when describing a voltage or current step function, rise time is the time taken by a signal to change from a specified low value to a specified high value. These values may be expressed as ratiosSee for example , and . or, equiva ...

while containing

distortion In signal processing, distortion is the alteration of the original shape (or other characteristic) of a signal. In communications and electronics it means the alteration of the waveform of an information-bearing signal, such as an audio signal ...

of the

signal A signal is both the process and the result of transmission of data over some media accomplished by embedding some variation. Signals are important in multiple subject fields including signal processing, information theory and biology. In ...

within acceptable limits. # Overshoot represents a

of the signal. # In circuit design, the goals of minimizing overshoot and of decreasing circuit

can conflict. # The magnitude of overshoot depends on time through a phenomenon called ''"

damping In physical systems, damping is the loss of energy of an oscillating system by dissipation. Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. Examples of damping include ...

."'' See illustration under step response''. # Overshoot often is associated with

settling time In control theory the settling time of a dynamical system such as an amplifier or other output device is the time elapsed from the application of an ideal instantaneous step input to the time at which the amplifier output has entered and remained ...

, how long it takes for the output to reach steady state; see step response. Also see the definition of ''overshoot'' in a control theory context.

Gibbs phenomenon

In the approximation of functions, ''overshoot'' is one term describing quality of approximation. When a function such as a square wave is represented by a summation of terms, for example, a

Fourier series A Fourier series () is an Series expansion, expansion of a periodic function into a sum of trigonometric functions. The Fourier series is an example of a trigonometric series. By expressing a function as a sum of sines and cosines, many problems ...

or an expansion in

orthogonal polynomials In mathematics, an orthogonal polynomial sequence is a family of polynomials such that any two different polynomials in the sequence are orthogonal In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geom ...

, the approximation of the function by a truncated number of terms in the series can exhibit overshoot, undershoot and ringing. The more terms retained in the series, the less pronounced the departure of the approximation from the function it represents. However, though the period of the oscillations decreases, their amplitude does not; this is known as the

Gibbs phenomenon In mathematics, the Gibbs phenomenon is the oscillatory behavior of the Fourier series of a piecewise continuously differentiable periodic function around a jump discontinuity. The Nth partial Fourier series of the function (formed by summing ...

. For the

Fourier transform In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...

, this can be modeled by approximating a

step function In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having on ...

by the integral up to a certain frequency, which yields the

sine integral In mathematics, trigonometric integrals are a indexed family, family of nonelementary integrals involving trigonometric functions. Sine integral The different sine integral definitions are \operatorname(x) = \int_0^x\frac\,dt \operato ...

. This can be interpreted as convolution with the

sinc function In mathematics, physics and engineering, the sinc function ( ), denoted by , has two forms, normalized and unnormalized.. In mathematics, the historical unnormalized sinc function is defined for by \operatorname(x) = \frac. Alternatively, ...

; in signal processing terms, this is a

Signal processing

, overshoot is when the output of a filter has a higher maximum value than the input, specifically for the step response, and frequently yields the related phenomenon of

ringing artifacts In signal processing, particularly digital image processing, ringing artifacts are Artifact (error), artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, t ...

. This occurs for instance in using the

sinc filter In signal processing, a sinc filter can refer to either a sinc-in-time filter whose impulse response is a sinc function and whose frequency response is rectangular, or to a sinc-in-frequency filter whose impulse response is rectangular and who ...

as an ideal ( brick-wall)

. The step response can be interpreted as the

convolution In mathematics (in particular, functional analysis), convolution is a operation (mathematics), mathematical operation on two function (mathematics), functions f and g that produces a third function f*g, as the integral of the product of the two ...

with the

impulse response In signal processing and control theory, the impulse response, or impulse response function (IRF), of a dynamic system is its output when presented with a brief input signal, called an impulse (). More generally, an impulse response is the reac ...

, which is a

. The overshoot and undershoot can be understood in this way: kernels are generally normalized to have integral 1, so they send constant functions to constant functions otherwise they have gain. The value of a convolution at a point is a

linear combination In mathematics, a linear combination or superposition is an Expression (mathematics), expression constructed from a Set (mathematics), set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of ''x'' a ...

of the input signal, with coefficients (weights) the values of the kernel. If a kernel is non-negative, such as for a

Gaussian kernel In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the base form f(x) = \exp (-x^2) and with parametric extension f(x) = a \exp\left( -\frac \right) for arbitrary real constants , and non-zero . It is ...

, then the value of the filtered signal will be a

convex combination In convex geometry and Vector space, vector algebra, a convex combination is a linear combination of point (geometry), points (which can be vector (geometric), vectors, scalar (mathematics), scalars, or more generally points in an affine sp ...

of the input values (the coefficients (the kernel) integrate to 1, and are non-negative), and will thus fall between the minimum and maximum of the input signal{{snd it will not undershoot or overshoot. If, on the other hand, the kernel assumes negative values, such as the sinc function, then the value of the filtered signal will instead be an

affine combination In mathematics, an affine combination of is a linear combination : \sum_^ = \alpha_ x_ + \alpha_ x_ + \cdots +\alpha_ x_, such that :\sum_^ =1. Here, can be elements ( vectors) of a vector space over a field , and the coefficients \alpha_ ...

of the input values, and may fall outside of the minimum and maximum of the input signal, resulting in undershoot and overshoot. Overshoot is often undesirable, particularly if it causes clipping, but is sometimes desirable in image sharpening, due to increasing

acutance In photography, acutance describes a subjective perception of visual acuity that is related to the edge contrast of an image. Acutance is related to the magnitude of the gradient of brightness. Due to the nature of the human visual system, an ...

(perceived sharpness).

Related concepts

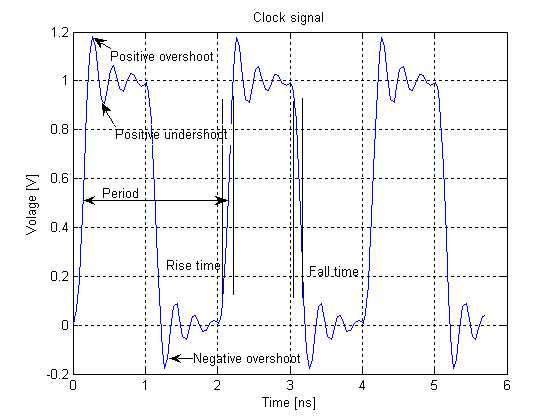
A closely related phenomenon is ringing, when, following overshoot, a signal then falls ''below'' its steady-state value, and then may bounce back above, taking some time to settle close to its steady-state value; this latter time is called the settle time. In

ecology Ecology () is the natural science of the relationships among living organisms and their Natural environment, environment. Ecology considers organisms at the individual, population, community (ecology), community, ecosystem, and biosphere lev ...

, overshoot is the analogous concept, where a population exceeds the

carrying capacity The carrying capacity of an ecosystem is the maximum population size of a biological species that can be sustained by that specific environment, given the food, habitat, water, and other resources available. The carrying capacity is defined as the ...

of a system.

References and notes

External links

Percentage overshoot calculator
Transient response characteristics Classical control theory