Intersection Over Union

picture info	Intersection Over Union The Jaccard index is a statistic used for gauging the Similarity measure, similarity and diversity index, diversity of Sample (statistics), sample sets. It is defined in general taking the ratio of two sizes (areas or volumes), the intersection size divided by the union size, also called intersection over union (IoU). It was developed by Grove Karl Gilbert in 1884 as his ratio of verification (v) and now is often called the critical success index in meteorology. It was later developed independently by Paul Jaccard, originally giving the French name (coefficient of community), and independently formulated again by Taffee Tadashi Tanimoto. Thus, it is also called Tanimoto index or Tanimoto coefficient in some fields. Overview The Jaccard index measures similarity between finite non-empty sample sets and is defined as the size of the intersection (set theory), intersection divided by the size of the Union (set theory), union of the sample sets: : J(A, B) = \frac = \frac. Note t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Object Detection Object detection is a computer technology related to computer vision and image processing that deals with detecting instances of semantic objects of a certain class (such as humans, buildings, or cars) in digital images and videos. Well-researched domains of object detection include face detection and pedestrian detection. Object detection has applications in many areas of computer vision, including image retrieval and video surveillance. Uses It is widely used in computer vision tasks such as image annotation, vehicle counting, activity recognition, face detection, face recognition, video object co-segmentation. It is also used in tracking objects, for example tracking a ball during a football match, tracking movement of a cricket bat, or tracking a person in a video. Often, the test images are sampled from a different data distribution, making the object detection task significantly more difficult. To address the challenges caused by the domain gap between training and test ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
picture info	Probability Measure In mathematics, a probability measure is a real-valued function defined on a set of events in a σ-algebra that satisfies Measure (mathematics), measure properties such as ''countable additivity''. The difference between a probability measure and the more general notion of measure (which includes concepts like area or volume) is that a probability measure must assign value 1 to the entire space. Intuitively, the additivity property says that the probability assigned to the union of two disjoint (mutually exclusive) events by the measure should be the sum of the probabilities of the events; for example, the value assigned to the outcome "1 or 2" in a throw of a dice should be the sum of the values assigned to the outcomes "1" and "2". Probability measures have applications in diverse fields, from physics to finance and biology. Definition The requirements for a set function \mu to be a probability measure on a σ-algebra are that: * \mu must return results in the unit interval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]
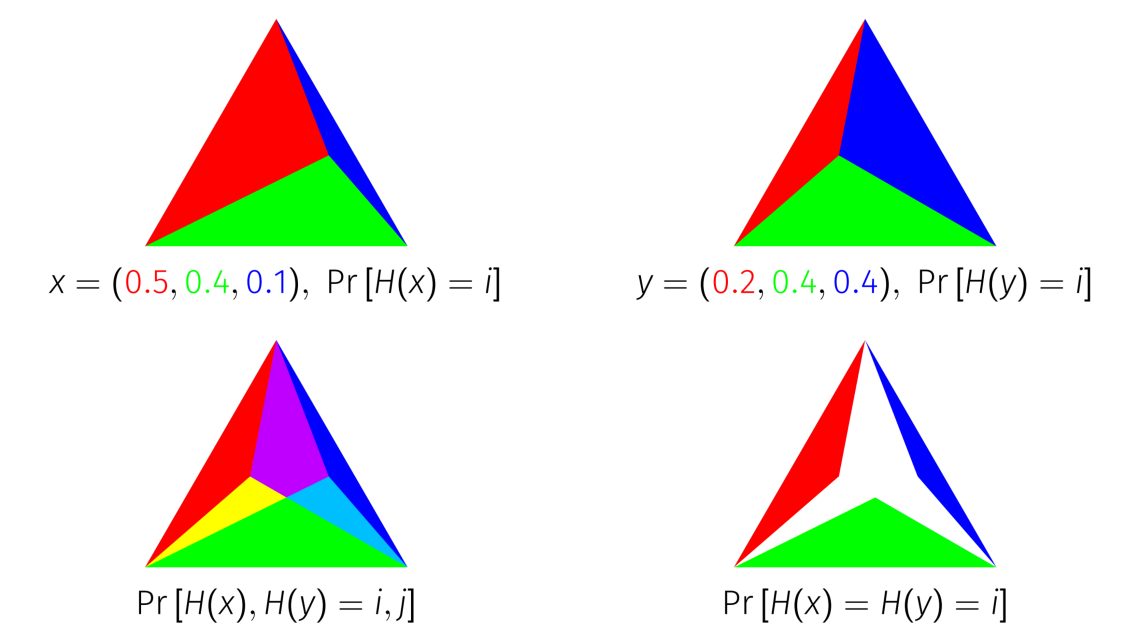
picture info	Geometric Interpretation Of The Probability Jaccard Index As Simplices Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a '' geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, a problem that was stated in terms of elementary arithmetic, and remained unsolved for several centuries. During t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu]