|
Probability Measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a σ-algebra that satisfies Measure (mathematics), measure properties such as ''countable additivity''. The difference between a probability measure and the more general notion of measure (which includes concepts like area or volume) is that a probability measure must assign value 1 to the entire space. Intuitively, the additivity property says that the probability assigned to the union of two disjoint (mutually exclusive) events by the measure should be the sum of the probabilities of the events; for example, the value assigned to the outcome "1 or 2" in a throw of a dice should be the sum of the values assigned to the outcomes "1" and "2". Probability measures have applications in diverse fields, from physics to finance and biology. Definition The requirements for a set function \mu to be a probability measure on a σ-algebra are that: * \mu must return results in the unit interval ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Financial Market
A financial market is a market in which people trade financial securities and derivatives at low transaction costs. Some of the securities include stocks and bonds, raw materials and precious metals, which are known in the financial markets as commodities. The term "market" is sometimes used for what are more strictly ''exchanges'', that is, organizations that facilitate the trade in financial securities, e.g., a stock exchange or commodity exchange. This may be a physical location (such as the New York Stock Exchange (NYSE), London Stock Exchange (LSE), Bombay Stock Exchange (BSE) or Johannesburg Stock Exchange ( JSE Limited)) or an electronic system such as NASDAQ. Much trading of stocks takes place on an exchange; still, corporate actions (mergers, spinoffs) are outside an exchange, while any two companies or people, for whatever reason, may agree to sell the stock from the one to the other without using an exchange. Trading of currencies and bonds is largely on a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ultrafilter
In the Mathematics, mathematical field of order theory, an ultrafilter on a given partially ordered set (or "poset") P is a certain subset of P, namely a Maximal element, maximal Filter (mathematics), filter on P; that is, a proper filter on P that cannot be enlarged to a bigger proper filter on P. If X is an arbitrary set, its power set (X), ordered by set inclusion, is always a Boolean algebra (structure), Boolean algebra and hence a poset, and ultrafilters on (X) are usually called X.If X happens to be partially ordered, too, particular care is needed to understand from the context whether an (ultra)filter on (X) or an (ultra)filter just on X is meant; both kinds of (ultra)filters are quite different. Some authors use "(ultra)filter ''of'' a partial ordered set" vs. "''on'' an arbitrary set"; i.e. they write "(ultra)filter on X" to abbreviate "(ultra)filter of (X)". An ultrafilter on a set X may be considered as a finitely additive 0-1-valued measure (mathematics), measure on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Amino Acid
Amino acids are organic compounds that contain both amino and carboxylic acid functional groups. Although over 500 amino acids exist in nature, by far the most important are the 22 α-amino acids incorporated into proteins. Only these 22 appear in the genetic code of life. Amino acids can be classified according to the locations of the core structural functional groups ( alpha- , beta- , gamma- amino acids, etc.); other categories relate to polarity, ionization, and side-chain group type ( aliphatic, acyclic, aromatic, polar, etc.). In the form of proteins, amino-acid '' residues'' form the second-largest component (water being the largest) of human muscles and other tissues. Beyond their role as residues in proteins, amino acids participate in a number of processes such as neurotransmitter transport and biosynthesis. It is thought that they played a key role in enabling life on Earth and its emergence. Amino acids are formally named by the IUPAC- IUBMB Joint Commi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequence Analysis
In bioinformatics, sequence analysis is the process of subjecting a DNA, RNA or peptide sequence to any of a wide range of analytical methods to understand its features, function, structure, or evolution. It can be performed on the entire genome, transcriptome or proteome of an organism, and can also involve only selected segments or regions, like tandem repeats and transposable elements. Methodologies used include sequence alignment, searches against biological databases, and others. Since the development of methods of high-throughput production of gene and protein sequences, the rate of addition of new sequences to the databases increased very rapidly. Such a collection of sequences does not, by itself, increase the scientist's understanding of the biology of organisms. However, comparing these new sequences to those with known functions is a key way of understanding the biology of an organism from which the new sequence comes. Thus, sequence analysis can be used to assign fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Biology
Mathematical and theoretical biology, or biomathematics, is a branch of biology which employs theoretical analysis, mathematical models and abstractions of living organisms to investigate the principles that govern the structure, development and behavior of the systems, as opposed to experimental biology which deals with the conduction of experiments to test scientific theories. The field is sometimes called mathematical biology or biomathematics to stress the mathematical side, or theoretical biology to stress the biological side. Theoretical biology focuses more on the development of theoretical principles for biology while mathematical biology focuses on the use of mathematical tools to study biological systems, even though the two terms interchange; overlapping as Artificial Immune Systems of Amorphous Computation. Mathematical biology aims at the mathematical representation and modeling of biological processes, using techniques and tools of applied mathematics. It ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Congruence Relation
In abstract algebra, a congruence relation (or simply congruence) is an equivalence relation on an algebraic structure (such as a group (mathematics), group, ring (mathematics), ring, or vector space) that is compatible with the structure in the sense that algebraic operations done with equivalent elements will yield equivalent elements. Every congruence relation has a corresponding Equivalence class, quotient structure, whose elements are the equivalence classes (or congruence classes) for the relation. Definition The definition of a congruence depends on the type of algebraic structure under consideration. Particular definitions of congruence can be made for group (mathematics), groups, ring (mathematics), rings, vector spaces, module (mathematics), modules, semigroups, lattice (order), lattices, and so forth. The common theme is that a congruence is an equivalence relation on an algebraic object that is compatible with the algebraic structure, in the sense that the operat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ..., information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Market
In economics, a complete market (aka Arrow-Debreu market or complete system of markets) is a market with two conditions: # Negligible transaction costs and therefore also perfect information, # Every asset in every possible state of the world has a price. In such a market, the complete set of possible bets on future states of the world can be constructed with existing assets without friction. Here, goods are state-contingent; that is, a good includes the time and state of the world in which it is consumed. For instance, an umbrella tomorrow if it rains is a distinct good from an umbrella tomorrow if it is clear. The study of complete markets is central to state-preference theory. The theory can be traced to the work of Kenneth Arrow (1964), Gérard Debreu Gérard Debreu (; 4 July 1921 – 31 December 2004) was a French-born economist and mathematician. Best known as a professor of economics at the University of California, Berkeley, where he began work in 1962, he won the 198 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Risk-free Rate
The risk-free rate of return, usually shortened to the risk-free rate, is the rate of return of a hypothetical investment with scheduled payments over a fixed period of time that is assumed to meet all payment obligations. Since the risk-free rate can be obtained with no risk, any other investment having some risk will have to have a higher rate of return in order to induce any investors to hold it. In practice, to infer the risk-free interest rate in a particular currency, market participants often choose the yield to maturity on a risk-free bond issued by a government of the same currency whose risks of default are so low as to be negligible. For example, the rate of return on zero-coupon Treasury bonds (T-bills) is sometimes seen as the risk-free rate of return in US dollars. Theoretical measurement As stated by Malcolm Kemp in chapter five of his book ''Market Consistency: Model Calibration in Imperfect Markets'', the risk-free rate means different things to different pe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
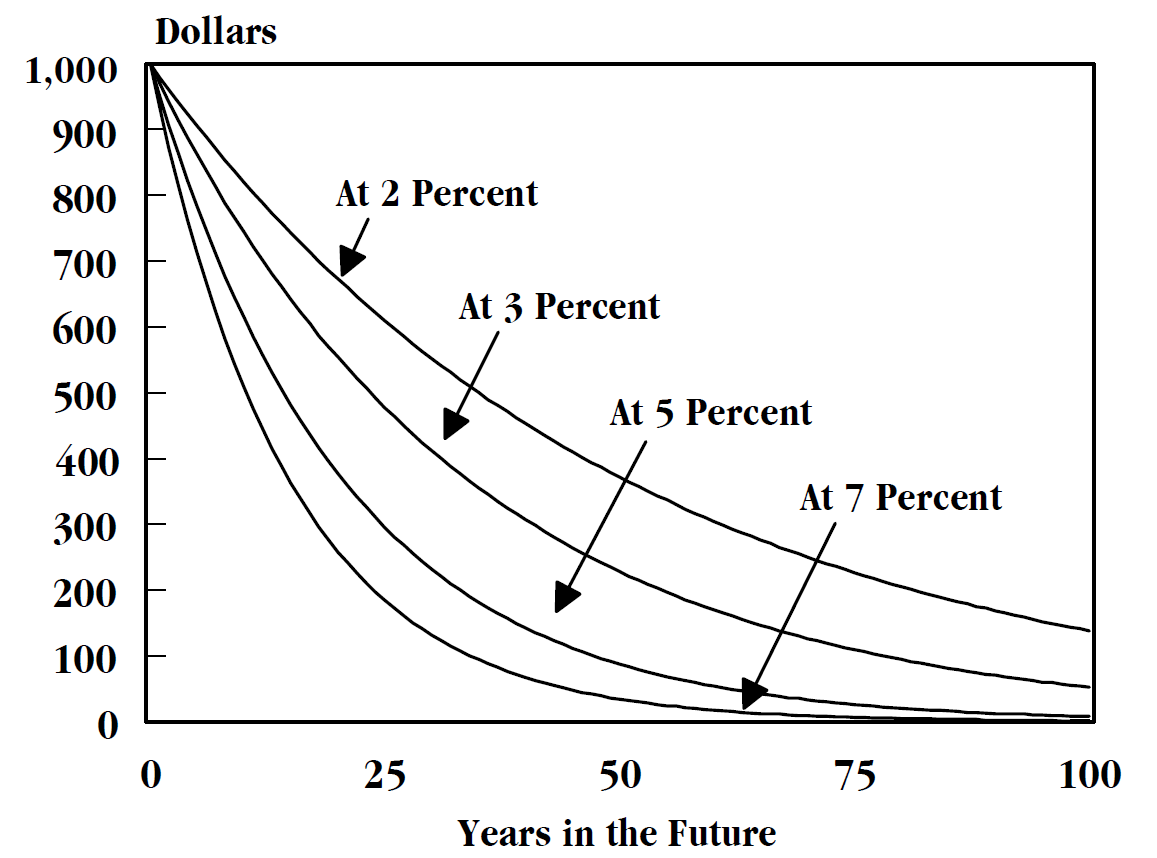
Discounted
In finance, discounting is a mechanism in which a debtor obtains the right to delay payments to a creditor, for a defined period of time, in exchange for a charge or fee.See "Time Value", "Discount", "Discount Yield", "Compound Interest", "Efficient Market", "Market Value" and "Opportunity Cost" in Downes, J. and Goodman, J. E. ''Dictionary of Finance and Investment Terms'', Baron's Financial Guides, 2003. Essentially, the party that owes money in the present purchases the right to delay the payment until some future date.See "Discount", "Compound Interest", "Efficient Markets Hypothesis", "Efficient Resource Allocation", "Pareto-Optimality", "Price", "Price Mechanism" and "Efficient Market" in Black, John, ''Oxford Dictionary of Economics'', Oxford University Press, 2002. This transaction is based on the fact that most people prefer current interest to delayed interest because of mortality effects, impatience effects, and salience effects. The discount, or charge, is the di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, expectation operator, mathematical expectation, mean, expectation value, or first Moment (mathematics), moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean, mean of the possible values a random variable can take, weighted by the probability of those outcomes. Since it is obtained through arithmetic, the expected value sometimes may not even be included in the sample data set; it is not the value you would expect to get in reality. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by Integral, integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |