|
H Theorem
In classical statistical mechanics, the ''H''-theorem, introduced by Ludwig Boltzmann in 1872, describes the tendency of the quantity ''H'' (defined below) to decrease in a nearly-ideal gas of molecules.L. Boltzmann,Weitere Studien über das Wärmegleichgewicht unter Gasmolekülen." Sitzungsberichte Akademie der Wissenschaften 66 (1872): 275-370. English translation: As this quantity ''H'' was meant to represent the entropy of thermodynamics, the ''H''-theorem was an early demonstration of the power of statistical mechanics as it claimed to derive the second law of thermodynamics—a statement about fundamentally irreversible processes—from reversible microscopic mechanics. It is thought to prove the second law of thermodynamics, albeit under the assumption of low-entropy initial conditions. The ''H''-theorem is a natural consequence of the kinetic equation derived by Boltzmann that has come to be known as Boltzmann's equation. The ''H''-theorem has led to considerable discuss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Mechanics
In physics, statistical mechanics is a mathematical framework that applies statistical methods and probability theory to large assemblies of microscopic entities. Sometimes called statistical physics or statistical thermodynamics, its applications include many problems in a wide variety of fields such as biology, neuroscience, computer science Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ..., information theory and sociology. Its main purpose is to clarify the properties of matter in aggregate, in terms of physical laws governing atomic motion. Statistical mechanics arose out of the development of classical thermodynamics, a field for which it was successful in explaining macroscopic physical properties—such as temperature, pressure, and heat capacity—in terms of microscop ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann Equation
The Boltzmann equation or Boltzmann transport equation (BTE) describes the statistical behaviour of a thermodynamic system not in a state of equilibrium; it was devised by Ludwig Boltzmann in 1872.Encyclopaedia of Physics (2nd Edition), R. G. Lerner, G. L. Trigg, VHC publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1, ISBN (VHC Inc.) 0-89573-752-3. The classic example of such a system is a fluid with temperature gradients in space causing heat to flow from hotter regions to colder ones, by the random but biased transport of the particles making up that fluid. In the modern literature the term Boltzmann equation is often used in a more general sense, referring to any kinetic equation that describes the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number. The equation arises not by analyzing the individual positions and momenta of each particle in the fluid but rather by considering a probability distribution for the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Information Entropy
In information theory, the entropy of a random variable quantifies the average level of uncertainty or information associated with the variable's potential states or possible outcomes. This measures the expected amount of information needed to describe the state of the variable, considering the distribution of probabilities across all potential states. Given a discrete random variable X, which may be any member x within the set \mathcal and is distributed according to p\colon \mathcal\to , 1/math>, the entropy is \Eta(X) := -\sum_ p(x) \log p(x), where \Sigma denotes the sum over the variable's possible values. The choice of base for \log, the logarithm, varies for different applications. Base 2 gives the unit of bits (or " shannons"), while base ''e'' gives "natural units" nat, and base 10 gives units of "dits", "bans", or " hartleys". An equivalent definition of entropy is the expected value of the self-information of a variable. The concept of information entropy was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluctuation Theorem
The fluctuation theorem (FT), which originated from statistical mechanics, deals with the relative probability that the Entropy (statistical thermodynamics), entropy of a system which is currently away from thermodynamic equilibrium (i.e., maximum entropy) will increase or decrease over a given amount of time. While the second law of thermodynamics predicts that the entropy of an isolated system should tend to increase until it reaches equilibrium, it became apparent after the discovery of statistical mechanics that the second law is only a statistical one, suggesting that there should always be some nonzero probability that the entropy of an isolated system might spontaneously ''decrease''; the fluctuation theorem precisely quantifies this probability. Statement Roughly, the fluctuation theorem relates to the probability distribution of the time-averaged irreversible entropy production, denoted \overline_t. The theorem states that, in systems away from equilibrium over a fi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Fluctuations
In statistical mechanics, thermal fluctuations are random deviations of an atomic system from its average state, that occur in a system at equilibrium.In statistical mechanics they are often simply referred to as fluctuations. All thermal fluctuations become larger and more frequent as the temperature increases, and likewise they decrease as temperature approaches absolute zero. Thermal fluctuations are a basic manifestation of the temperature of systems: A system at nonzero temperature does not stay in its equilibrium microscopic state, but instead randomly samples all possible states, with probabilities given by the Boltzmann distribution. Thermal fluctuations generally affect all the degrees of freedom of a system: There can be random vibrations (phonons), random rotations ( rotons), random electronic excitations, and so forth. Thermodynamic variables, such as pressure, temperature, or entropy, likewise undergo thermal fluctuations. For example, for a system that has an equ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isolated System
In physical science, an isolated system is either of the following: # a physical system so far removed from other systems that it does not interact with them. # a thermodynamic system enclosed by rigid immovable walls through which neither mass nor energy can pass. Though subject internally to its own gravity, an isolated system is usually taken to be outside the reach of external gravitational and other long-range forces. This can be contrasted with what (in the more common terminology used in thermodynamics) is called a closed system, being enclosed by selective walls through which energy can pass as heat or work, but not matter; and with an open system, which both matter and energy can enter or exit, though it may have variously impermeable walls in parts of its boundaries. An isolated system obeys the conservation law that its total energy–mass stays constant. Most often, in thermodynamics, mass and energy are treated as separately conserved. Because of the requir ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poincaré Recurrence
Poincaré is a French surname. Notable people with the surname include: * Henri Poincaré (1854–1912), French physicist, mathematician and philosopher of science * Henriette Poincaré (1858–1943), wife of Prime Minister Raymond Poincaré * Lucien Poincaré (1862–1920), physicist, brother of Raymond and cousin of Henri * Raymond Poincaré (1860–1934), French Prime Minister or President ''inter alia'' from 1913 to 1920, cousin of Henri See also *List of things named after Henri Poincaré In physics and mathematics, a number of ideas are named after Henri Poincaré: * Euler–Poincaré characteristic * Hilbert–Poincaré series * Poincaré–Bendixson theorem * Poincaré–Birkhoff theorem * Poincaré–Birkhoff–Witt theorem, ... * {{DEFAULTSORT:Poincare French-language surnames ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ernst Zermelo
Ernst Friedrich Ferdinand Zermelo (; ; 27 July 187121 May 1953) was a German logician and mathematician, whose work has major implications for the foundations of mathematics. He is known for his role in developing Zermelo–Fraenkel set theory, Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem. Furthermore, his 1929 work on ranking chess players is the first description of a model for Pairwise comparison (psychology), pairwise comparison that continues to have a profound impact on various applied fields utilizing this method. Life Ernst Zermelo graduated from Berlin's Luisenstädtisches Gymnasium (now ) in 1889. He then studied mathematics, physics and philosophy at the University of Berlin, the University of Halle, and the University of Freiburg. He finished his doctorate in 1894 at the University of Berlin, awarded for a dissertation on the calculus of variations (''Untersuchungen zur Variationsrechnung''). Zermelo remained at the University of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
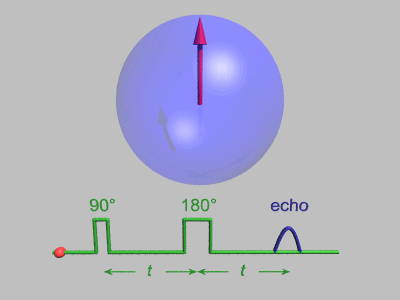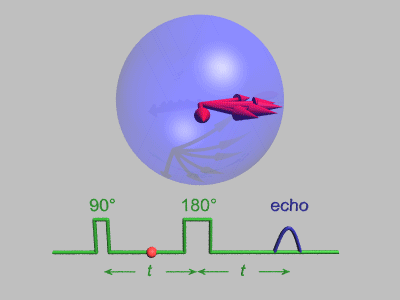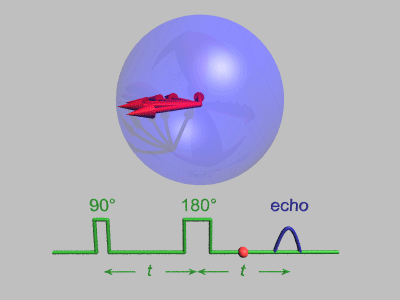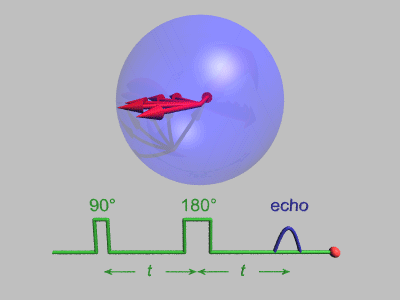
Spin Echo
In magnetic resonance, a spin echo or Hahn echo is the refocusing of spin magnetisation by a pulse of resonant electromagnetic radiation. Modern nuclear magnetic resonance (NMR) and magnetic resonance imaging (MRI) make use of this effect. The NMR signal observed following an initial excitation pulse decays with time due to both spin relaxation and any ''inhomogeneous'' effects which cause spins in the sample to precess at different rates. The first of these, relaxation, leads to an irreversible loss of magnetisation. But the inhomogeneous dephasing can be removed by applying a 180° ''inversion'' pulse that inverts the magnetisation vectors. Examples of inhomogeneous effects include a magnetic field gradient and a distribution of chemical shifts. If the inversion pulse is applied after a period ''t'' of dephasing, the inhomogeneous evolution will rephase to form an echo at time 2''t''. In simple cases, the intensity of the echo relative to the initial signal is given by '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boltzmann's Entropy Formula
In statistical mechanics, Boltzmann's entropy formula (also known as the Boltzmann–Planck equation, not to be confused with the more general Boltzmann equation, which is a partial differential equation) is a probability equation relating the entropy S, also written as S_\mathrm, of an ideal gas to the multiplicity (commonly denoted as \Omega or W), the number of real microstates corresponding to the gas's macrostate: where k_\mathrm B is the Boltzmann constant (also written as simply k) and equal to 1.380649 × 10−23 J/K, and \ln is the natural logarithm function (or log base e, as in the image above). In short, the Boltzmann formula shows the relationship between entropy and the number of ways the atoms or molecules of a certain kind of thermodynamic system can be arranged. History The equation was originally formulated by Ludwig Boltzmann between 1872 and 1875, but later put into its current form by Max Planck in about 1900. To quote Planck, "the logarithmic c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Begs The Question
Begging (also known in North America as panhandling) is the practice of imploring others to grant a favor, often a gift of money, with little or no expectation of reciprocation. A person doing such is called a beggar or panhandler. Beggars may operate in public places such as transport routes, urban parks, and markets. Besides money, they may also ask for food, drink, cigarettes or other small items. Internet begging is the modern practice of asking people to give money to others via the Internet, rather than in person. Internet begging may encompass requests for help meeting basic needs such as medical care and shelter, as well as requests for people to pay for vacations, school trips, and other things that the beggar wants but cannot ostensibly afford. Beggars differ from religious mendicants in that some mendicants do not ask for money. Their subsistence is reciprocated by providing society with various forms of religious service, moral education, and preservation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Loschmidt's Paradox
In physics, Loschmidt's paradox (named for Josef Loschmidt), also known as the reversibility paradox, irreversibility paradox, or ' (), is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics. This puts the time reversal symmetry of (almost) all known low-level fundamental physical processes at odds with any attempt to infer from them the second law of thermodynamics, which describes the behaviour of macroscopic systems. Both of these are well-accepted principles in physics, with sound observational and theoretical support, yet they seem to be in conflict, hence the paradox. Origin Josef Loschmidt's criticism was provoked by the H-theorem of Boltzmann, which employed kinetic theory to explain the increase of entropy in an ideal gas from a non-equilibrium state, when the molecules of the gas are allowed to collide. In 1876, Loschmidt pointed out that if there is a motion of a system from time ''t''0 to time ''t''1 to tim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |