|
Four Fours
Four fours is a mathematical puzzle, the goal of which is to find the simplest mathematical expression for every whole number from 0 to some maximum, using only common mathematical symbols and the digit four. No other digit is allowed. Most versions of the puzzle require that each expression have exactly four fours, but some variations require that each expression have some ''minimum'' number of fours. The puzzle requires skill and mathematical reasoning. The first printed occurrence of the specific problem of four fours is in '' Knowledge: An Illustrated Magazine of Science'' in 1881. A similar problem involving arranging four identical digits to equal a certain amount was given in Thomas Dilworth's popular 1734 textbook '' The Schoolmaster's Assistant, Being a Compendium of Arithmetic Both Practical and Theoretical''. W. W. Rouse Ball described it in the 6th edition (1914) of his ''Mathematical Recreations and Essays''. In this book it is described as a "traditional recreation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Puzzle
Mathematical puzzles make up an integral part of recreational mathematics. They have specific rules, but they do not usually involve competition between two or more players. Instead, to solve such a puzzle, the solver must find a solution that satisfies the given conditions. Mathematical puzzles require mathematics to solve them. Logic puzzles are a common type of mathematical puzzle. Conway's Game of Life and fractals, as two examples, may also be considered mathematical puzzles even though the solver interacts with them only at the beginning by providing a set of initial conditions. After these conditions are set, the rules of the puzzle determine all subsequent changes and moves. Many of the puzzles are well known because they were discussed by Martin Gardner in his "Mathematical Games" column in Scientific American. Mathematical puzzles are sometimes used to motivate students in teaching elementary school Mathematical problem, math problem solving techniques.Kulkarni, DEnjoying ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal Function
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an involution). Multiplying by a number is the same as dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yields the original number (since the product of the number and its reciprocal is 1). The term ''reciproca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial: \begin n! &= n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times 3 \times 2 \times 1 \\ &= n\times(n-1)!\\ \end For example, 5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. The value of 0! is 1, according to the convention for an empty product. Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book ''Sefer Yetzirah''. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of n distinct objects: there In mathematical analysis, factorials are used in power series for the ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplicative Inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a rational number, fraction ''a''/''b'' is ''b''/''a''. For the multiplicative inverse of a real number, divide 1 by the number. For example, the reciprocal of 5 is one fifth (1/5 or 0.2), and the reciprocal of 0.25 is 1 divided by 0.25, or 4. The reciprocal function, the Function (mathematics), function ''f''(''x'') that maps ''x'' to 1/''x'', is one of the simplest examples of a function which is its own inverse (an Involution (mathematics), involution). Multiplying by a number is the same as Division (mathematics), dividing by its reciprocal and vice versa. For example, multiplication by 4/5 (or 0.8) will give the same result as division by 5/4 (or 1.25). Therefore, multiplication by a number followed by multiplication by its reciprocal yie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Arithmetic
Elementary arithmetic is a branch of mathematics involving addition, subtraction, multiplication, and Division (mathematics), division. Due to its low level of abstraction, broad range of application, and position as the foundation of all mathematics, elementary arithmetic is generally the first branch of mathematics taught in schools. Numeral systems In numeral system, numeral systems, Numerical digit, digits are characters used to represent the value of numbers. An example of a numeral system is the predominantly used Hindu–Arabic numeral system, Indo-Arabic numeral system (0 to 9), which uses a Base 10, decimal positional notation. Other numeral systems include the Kaktovik numerals, Kaktovik system (often used in the Eskimo-Aleut languages of Alaska, Canada, and Greenland), and is a vigesimal positional notation system. Regardless of the numeral system used, the results of arithmetic operations are unaffected. Successor function and ordering In elementary arithmetic, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , then is the logarithm of to base , written , so . As a single-variable function, the logarithm to base is the inverse of exponentiation with base . The logarithm base is called the ''decimal'' or ''common'' logarithm and is commonly used in science and engineering. The ''natural'' logarithm has the number as its base; its use is widespread in mathematics and physics because of its very simple derivative. The ''binary'' logarithm uses base and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written . Logarithms were introduced by John Napier in 1614 as a means of simplifying calculation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Successor Function
In mathematics, the successor function or successor operation sends a natural number to the next one. The successor function is denoted by ''S'', so ''S''(''n'') = ''n'' +1. For example, ''S''(1) = 2 and ''S''(2) = 3. The successor function is one of the basic components used to build a primitive recursive function. Successor operations are also known as zeration in the context of a zeroth hyperoperation: H0(''a'', ''b'') = 1 + ''b''. In this context, the extension of zeration is addition, which is defined as repeated succession. Overview The successor function is part of the formal language used to state the Peano axioms, which formalise the structure of the natural numbers. In this formalisation, the successor function is a primitive operation on the natural numbers, in terms of which the standard natural numbers and addition are defined. For example, 1 is defined to be ''S''(0), and addition on natural numbers is defined recursively by: : This can be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percent
In mathematics, a percentage () is a number or ratio expressed as a fraction of 100. It is often denoted using the ''percent sign'' (%), although the abbreviations ''pct.'', ''pct'', and sometimes ''pc'' are also used. A percentage is a dimensionless number (pure number), primarily used for expressing proportions, but percent is nonetheless a unit of measurement in its orthography and usage. Examples For example, 45% (read as "forty-five percent") is equal to the fraction , or 0.45. Percentages are often used to express a proportionate part of a total. (Similarly, one can also express a number as a fraction of 1,000, using the term "per mille" or the symbol "".) Example 1 If 50% of the total number of students in the class are male, that means that 50 out of every 100 students are male. If there are 500 students, then 250 of them are male. Example 2 An increase of $0.15 on a price of $2.50 is an increase by a fraction of = 0.06. Expressed as a percentage, this is a 6% ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gamma Function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined for all complex numbers z except non-positive integers, and for every positive integer z=n, \Gamma(n) = (n-1)!\,.The gamma function can be defined via a convergent improper integral for complex numbers with positive real part: \Gamma(z) = \int_0^\infty t^ e^\textt, \ \qquad \Re(z) > 0\,.The gamma function then is defined in the complex plane as the analytic continuation of this integral function: it is a meromorphic function which is holomorphic function, holomorphic except at zero and the negative integers, where it has simple Zeros and poles, poles. The gamma function has no zeros, so the reciprocal gamma function is an entire function. In fact, the gamma function corresponds to the Mellin transform of the negative exponential functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube Root
In mathematics, a cube root of a number is a number that has the given number as its third power; that is y^3=x. The number of cube roots of a number depends on the number system that is considered. Every real number has exactly one real cube root that is denoted \sqrt /math> and called the ''real cube root'' of or simply ''the cube root'' of in contexts where complex numbers are not considered. For example, the real cube roots of and are respectively and . The real cube root of an integer or of a rational number is generally not a rational number, neither a constructible number. Every nonzero real or complex number has exactly three cube roots that are complex numbers. If the number is real, one of the cube roots is real and the two other are nonreal complex conjugate numbers. Otherwise, the three cube roots are all nonreal. For example, the real cube root of is and the other cube roots of are -1+i\sqrt 3 and -1-i\sqrt 3. The three cube roots of are 3i, \tfrac-\ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
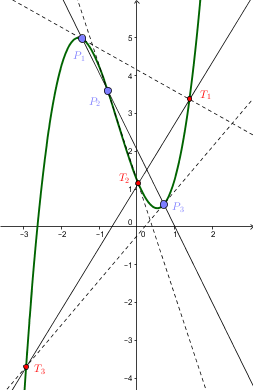
Cubic Function
In mathematics, a cubic function is a function of the form f(x)=ax^3+bx^2+cx+d, that is, a polynomial function of degree three. In many texts, the ''coefficients'' , , , and are supposed to be real numbers, and the function is considered as a real function that maps real numbers to real numbers or as a complex function that maps complex numbers to complex numbers. In other cases, the coefficients may be complex numbers, and the function is a complex function that has the set of the complex numbers as its codomain, even when the domain is restricted to the real numbers. Setting produces a cubic equation of the form :ax^3+bx^2+cx+d=0, whose solutions are called roots of the function. The derivative of a cubic function is a quadratic function. A cubic function with real coefficients has either one or three real roots ( which may not be distinct); all odd-degree polynomials with real coefficients have at least one real root. The graph of a cubic function always has a single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Function
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations ''x''^2 ( caret) or ''x''**2 may be used in place of ''x''2. The adjective which corresponds to squaring is '' quadratic''. The square of an integer may also be called a '' square number'' or a ''perfect square''. In algebra, the operation of squaring is often generalized to polynomials, other expressions, or values in systems of mathematical values other than the numbers. For instance, the square of the linear polynomial is the quadratic polynomial . One of the important properties of squaring, for numbers as well as in many other mathematical systems, is tha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |