
In
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the logarithm of a number is the
exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , then is the logarithm of to base , written , so . As a single-variable function, the logarithm to base is the
inverse of
exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
with base .
The logarithm base is called the ''decimal'' or
''common'' logarithm and is commonly used in science and engineering. The
''natural'' logarithm has the number
as its base; its use is widespread in mathematics and
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
because of its very simple
derivative. The
''binary'' logarithm uses base and is widely used in
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
,
information theory,
music theory
Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first is the "Elements of music, ...
, and
photography
Photography is the visual arts, art, application, and practice of creating images by recording light, either electronically by means of an image sensor, or chemically by means of a light-sensitive material such as photographic film. It is empl ...
. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written .
Logarithms were introduced by
John Napier
John Napier of Merchiston ( ; Latinisation of names, Latinized as Ioannes Neper; 1 February 1550 – 4 April 1617), nicknamed Marvellous Merchiston, was a Scottish landowner known as a mathematician, physicist, and astronomer. He was the 8 ...
in 1614 as a means of simplifying calculations. They were rapidly adopted by
navigators, scientists, engineers,
surveyors, and others to perform high-accuracy computations more easily. Using
logarithm tables, tedious multi-digit multiplication steps can be replaced by table look-ups and simpler addition. This is possible because the logarithm of a
product is the
sum of the logarithms of the factors:
provided that , and are all positive and . The
slide rule, also based on logarithms, allows quick calculations without tables, but at lower precision. The present-day notion of logarithms comes from
Leonhard Euler, who connected them to the
exponential function in the 18th century, and who also introduced the letter as the base of natural logarithms.
Logarithmic scale
A logarithmic scale (or log scale) is a method used to display numerical data that spans a broad range of values, especially when there are significant differences among the magnitudes of the numbers involved.
Unlike a linear Scale (measurement) ...
s reduce wide-ranging quantities to smaller scopes. For example, the
decibel (dB) is a
unit used to express
ratio as logarithms, mostly for signal power and amplitude (of which
sound pressure is a common example). In chemistry,
pH is a logarithmic measure for the
acid
An acid is a molecule or ion capable of either donating a proton (i.e. Hydron, hydrogen cation, H+), known as a Brønsted–Lowry acid–base theory, Brønsted–Lowry acid, or forming a covalent bond with an electron pair, known as a Lewis ...
ity of an
aqueous solution. Logarithms are commonplace in scientific
formulae, and in measurements of the
complexity of algorithms and of geometric objects called
fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
s. They help to describe
frequency ratios of
musical intervals, appear in formulas counting
prime number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime ...
s or
approximating factorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times ...
s, inform some models in
psychophysics, and can aid in
forensic accounting.
The concept of logarithm as the inverse of exponentiation extends to other mathematical structures as well. However, in general settings, the logarithm tends to be a multi-valued function. For example, the
complex logarithm is the multi-valued
inverse of the complex exponential function. Similarly, the
discrete logarithm is the multi-valued inverse of the exponential function in finite groups; it has uses in
public-key cryptography.
Motivation

Addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
,
multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
, and
exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
are three of the most fundamental arithmetic operations. The inverse of addition is
subtraction, and the inverse of multiplication is
division. Similarly, a logarithm is the inverse operation of
exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
. Exponentiation is when a number , the ''base'', is raised to a certain power , the ''exponent'', to give a value ; this is denoted
For example, raising to the power of gives :
The logarithm of base is the inverse operation, that provides the output from the input . That is,
is equivalent to
if is a positive
real number. (If is not a positive real number, both exponentiation and logarithm can be defined but may take several values, which makes definitions much more complicated.)
One of the main historical motivations of introducing logarithms is the formula
by which
tables of logarithms allow multiplication and division to be reduced to addition and subtraction, a great aid to calculations before the invention of computers.
Definition
Given a positive
real number such that , the ''logarithm'' of a positive real number with respect to base is the exponent by which must be raised to yield . In other words, the logarithm of to base is the unique real number such that
.
The logarithm is denoted "" (pronounced as "the logarithm of to base ", "the logarithm of ", or most commonly "the log, base , of ").
An equivalent and more succinct definition is that the function is the
inverse function to the function
.
Examples
* , since .
* Logarithms can also be negative:
since
* is approximately 2.176, which lies between 2 and 3, just as 150 lies between and .
* For any base , and , since and , respectively.
Logarithmic identities
Several important formulas, sometimes called ''logarithmic identities'' or ''logarithmic laws'', relate logarithms to one another.
Product, quotient, power, and root
The logarithm of a product is the sum of the logarithms of the numbers being multiplied; the logarithm of the ratio of two numbers is the difference of the logarithms. The logarithm of the -th power of a number is times the logarithm of the number itself; the logarithm of a -th root is the logarithm of the number divided by . The following table lists these identities with examples. Each of the identities can be derived after substitution of the logarithm definitions
or
in the left hand sides. In the following formulas, and are
positive real numbers and is an integer greater than 1.
Change of base
The logarithm can be computed from the logarithms of and with respect to an arbitrary base using the following formula:
Typical
scientific calculators calculate the logarithms to bases 10 and . Logarithms with respect to any base can be determined using either of these two logarithms by the previous formula:
Given a number and its logarithm to an unknown base , the base is given by:
which can be seen from taking the defining equation
to the power of
Particular bases

Among all choices for the base, three are particularly common. These are , (the
irrational mathematical constant and (the
binary logarithm). In
mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series ( ...
, the logarithm base is widespread because of analytical properties explained below. On the other hand, logarithms (the
common logarithm) are easy to use for manual calculations in the
decimal number system:
Thus, is related to the number of
decimal digits of a positive integer : The number of digits is the smallest
integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
strictly bigger than
For example, is approximately 3.78 . The
next integer above it is 4, which is the number of digits of 5986. Both the natural logarithm and the binary logarithm are used in
information theory, corresponding to the use of
nats or
bits as the fundamental units of information, respectively.
Binary logarithms are also used in
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
, where the
binary system is ubiquitous; in
music theory
Music theory is the study of theoretical frameworks for understanding the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory": The first is the "Elements of music, ...
, where a pitch ratio of two (the
octave) is ubiquitous and the number of
cents between any two pitches is a scaled version of the binary logarithm, or log 2 times 1200, of the pitch ratio (that is, 100 cents per
semitone in
conventional equal temperament), or equivalently the log base and in
photography
Photography is the visual arts, art, application, and practice of creating images by recording light, either electronically by means of an image sensor, or chemically by means of a light-sensitive material such as photographic film. It is empl ...
rescaled base 2 logarithms are used to measure
exposure values,
light levels,
exposure times, lens
apertures, and
film speeds in "stops".
The abbreviation is often used when the intended base can be inferred based on the context or discipline, or when the base is indeterminate or immaterial. Common logarithms (base 10), historically used in logarithm tables and slide rules, are a basic tool for measurement and computation in many areas of science and engineering; in these contexts still often means the base ten logarithm. In mathematics usually refers to the natural logarithm (base ).
In computer science and information theory, often refers to binary logarithms (base 2). The following table lists common notations for logarithms to these bases. The "ISO notation" column lists designations suggested by the
International Organization for Standardization
The International Organization for Standardization (ISO ; ; ) is an independent, non-governmental, international standard development organization composed of representatives from the national standards organizations of member countries.
M ...
.
History
The history of logarithms in seventeenth-century Europe saw the discovery of a new
function that extended the realm of analysis beyond the scope of algebraic methods. The method of logarithms was publicly propounded by
John Napier
John Napier of Merchiston ( ; Latinisation of names, Latinized as Ioannes Neper; 1 February 1550 – 4 April 1617), nicknamed Marvellous Merchiston, was a Scottish landowner known as a mathematician, physicist, and astronomer. He was the 8 ...
in 1614, in a book titled ''
Mirifici Logarithmorum Canonis Descriptio'' (''Description of the Wonderful Canon of Logarithms''). Prior to Napier's invention, there had been other techniques of similar scopes, such as the
prosthaphaeresis or the use of tables of progressions, extensively developed by
Jost Bürgi around 1600.
Napier coined the term for logarithm in Middle Latin, , literally meaning , derived from the Greek + .
The
common logarithm of a number is the index of that power of ten which equals the number. Speaking of a number as requiring so many figures is a rough allusion to common logarithm, and was referred to by
Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
as the "order of a number". The first real logarithms were heuristic methods to turn multiplication into addition, thus facilitating rapid computation. Some of these methods used tables derived from trigonometric identities. Such methods are called
prosthaphaeresis.
Invention of the
function now known as the
natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
began as an attempt to perform a
quadrature of a rectangular
hyperbola by
Grégoire de Saint-Vincent, a Belgian Jesuit residing in Prague. Archimedes had written ''
The Quadrature of the Parabola'' in the third century BC, but a quadrature for the hyperbola eluded all efforts until Saint-Vincent published his results in 1647. The relation that the logarithm provides between a
geometric progression in its
argument
An argument is a series of sentences, statements, or propositions some of which are called premises and one is the conclusion. The purpose of an argument is to give reasons for one's conclusion via justification, explanation, and/or persu ...
and an
arithmetic progression of values, prompted
A. A. de Sarasa to make the connection of Saint-Vincent's quadrature and the tradition of logarithms in
prosthaphaeresis, leading to the term "hyperbolic logarithm", a synonym for natural logarithm. Soon the new function was appreciated by
Christiaan Huygens
Christiaan Huygens, Halen, Lord of Zeelhem, ( , ; ; also spelled Huyghens; ; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution ...
, and
James Gregory. The notation was adopted by
Gottfried Wilhelm Leibniz
Gottfried Wilhelm Leibniz (or Leibnitz; – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat who is credited, alongside Sir Isaac Newton, with the creation of calculus in addition to ...
in 1675, and the next year he connected it to the
integral
In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...
Before Euler developed his modern conception of complex natural logarithms,
Roger Cotes had a nearly equivalent result when he showed in 1714 that
Logarithm tables, slide rules, and historical applications
By simplifying difficult calculations before calculators and computers became available, logarithms contributed to the advance of science, especially
astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest includ ...
. They were critical to advances in
surveying,
celestial navigation, and other domains.
Pierre-Simon Laplace called logarithms
... admirable artifice which, by reducing to a few days the labour of many months, doubles the life of the astronomer, and spares him the errors and disgust inseparable from long calculations.
As the function is the inverse function of , it has been called an antilogarithm. Nowadays, this function is more commonly called an
exponential function.
Log tables
A key tool that enabled the practical use of logarithms was the ''
table of logarithms''. The first such table was compiled by
Henry Briggs in 1617, immediately after Napier's invention but with the innovation of using 10 as the base. Briggs' first table contained the
common logarithms of all integers in the range from 1 to 1000, with a precision of 14 digits. Subsequently, tables with increasing scope were written. These tables listed the values of for any number in a certain range, at a certain precision. Base-10 logarithms were universally used for computation, hence the name common logarithm, since numbers that differ by factors of 10 have logarithms that differ by integers. The common logarithm of can be separated into an
integer part and a
fractional part, known as the characteristic and
mantissa. Tables of logarithms need only include the mantissa, as the characteristic can be easily determined by counting digits from the decimal point. The characteristic of is one plus the characteristic of , and their mantissas are the same. Thus using a three-digit log table, the logarithm of 3542 is approximated by
Greater accuracy can be obtained by
interpolation:
The value of can be determined by reverse look up in the same table, since the logarithm is a
monotonic function.
Computations
The product and quotient of two positive numbers and ' were routinely calculated as the sum and difference of their logarithms. The product or quotient came from looking up the antilogarithm of the sum or difference, via the same table:
and
For manual calculations that demand any appreciable precision, performing the lookups of the two logarithms, calculating their sum or difference, and looking up the antilogarithm is much faster than performing the multiplication by earlier methods such as
prosthaphaeresis, which relies on
trigonometric identities.
Calculations of powers and
roots are reduced to multiplications or divisions and lookups by
and
Trigonometric calculations were facilitated by tables that contained the common logarithms of
trigonometric functions.
Slide rules
Another critical application was the slide rule, a pair of logarithmically divided scales used for calculation. The non-sliding logarithmic scale,
Gunter's rule, was invented shortly after Napier's invention.
William Oughtred enhanced it to create the slide rule—a pair of logarithmic scales movable with respect to each other. Numbers are placed on sliding scales at distances proportional to the differences between their logarithms. Sliding the upper scale appropriately amounts to mechanically adding logarithms, as illustrated here:
For example, adding the distance from 1 to 2 on the lower scale to the distance from 1 to 3 on the upper scale yields a product of 6, which is read off at the lower part. The slide rule was an essential calculating tool for engineers and scientists until the 1970s, because it allows, at the expense of precision, much faster computation than techniques based on tables.
Analytic properties
A deeper study of logarithms requires the concept of a ''
function''. A function is a rule that, given one number, produces another number. An example is the function producing the -th power of from any real number , where the base is a fixed number. This function is written as . When is positive and unequal to 1, we show below that is invertible when considered as a function from the reals to the positive reals.
Existence
Let be a positive real number not equal to 1 and let .
It is a standard result in real analysis that any continuous strictly monotonic function is bijective between its domain and range. This fact follows from the
intermediate value theorem.
[, section III.3] Now, is
strictly increasing (for ), or strictly decreasing (for ),
is continuous, has domain
, and has range
. Therefore, is a bijection from
to
. In other words, for each positive real number , there is exactly one real number such that
.
We let
denote the inverse of . That is, is the unique real number such that
. This function is called the base- ''logarithm function'' or ''logarithmic function'' (or just ''logarithm'').
Characterization by the product formula
The function can also be essentially characterized by the product formula
More precisely, the logarithm to any base is the only
increasing function ''f'' from the positive reals to the reals satisfying and
Graph of the logarithm function

As discussed above, the function is the inverse to the exponential function
. Therefore, their
graphs correspond to each other upon exchanging the - and the -coordinates (or upon reflection at the diagonal line ), as shown at the right: a point on the graph of yields a point on the graph of the logarithm and vice versa. As a consequence,
diverges to infinity (gets bigger than any given number) if grows to infinity, provided that is greater than one. In that case, is an
increasing function. For , tends to minus infinity instead. When approaches zero, goes to minus infinity for (plus infinity for , respectively).
Derivative and antiderivative

Analytic properties of functions pass to their inverses.
Thus, as is a continuous and
differentiable function, so is . Roughly, a continuous function is differentiable if its graph has no sharp "corners". Moreover, as the
derivative of evaluates to by the properties of the
exponential function, the
chain rule implies that the derivative of is given by
That is, the
slope of the
tangent touching the graph of the logarithm at the point equals .
The derivative of is ; this implies that is the unique
antiderivative of that has the value 0 for . It is this very simple formula that motivated to qualify as "natural" the natural logarithm; this is also one of the main reasons of the importance of the
constant .
The derivative with a generalized functional argument is
The quotient at the right hand side is called the
logarithmic derivative of '. Computing by means of the derivative of is known as
logarithmic differentiation. The antiderivative of the
natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
is:
Related formulas, such as antiderivatives of logarithms to other bases can be derived from this equation using the change of bases.
Integral representation of the natural logarithm

The
natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
of can be defined as the
definite integral:
This definition has the advantage that it does not rely on the exponential function or any trigonometric functions; the definition is in terms of an integral of a simple reciprocal. As an integral, equals the area between the -axis and the graph of the function , ranging from to . This is a consequence of the
fundamental theorem of calculus and the fact that the derivative of is . Product and power logarithm formulas can be derived from this definition. For example, the product formula is deduced as:
The equality (1) splits the integral into two parts, while the equality (2) is a change of variable (). In the illustration below, the splitting corresponds to dividing the area into the yellow and blue parts. Rescaling the left hand blue area vertically by the factor and shrinking it by the same factor horizontally does not change its size. Moving it appropriately, the area fits the graph of the function again. Therefore, the left hand blue area, which is the integral of from to is the same as the integral from 1 to . This justifies the equality (2) with a more geometric proof.

The power formula may be derived in a similar way:
The second equality uses a change of variables (
integration by substitution
In calculus, integration by substitution, also known as ''u''-substitution, reverse chain rule or change of variables, is a method for evaluating integrals and antiderivatives. It is the counterpart to the chain rule for differentiation, and c ...
), .
The sum over the reciprocals of natural numbers,
is called the
harmonic series. It is closely tied to the
natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
: as tends to
infinity
Infinity is something which is boundless, endless, or larger than any natural number. It is denoted by \infty, called the infinity symbol.
From the time of the Ancient Greek mathematics, ancient Greeks, the Infinity (philosophy), philosophic ...
, the difference,
converges (i.e. gets arbitrarily close) to a number known as the
Euler–Mascheroni constant . This relation aids in analyzing the performance of algorithms such as
quicksort.
Transcendence of the logarithm
Real numbers that are not
algebraic are called
transcendental; for example,
and ''
e'' are such numbers, but
is not.
Almost all
In mathematics, the term "almost all" means "all but a negligible quantity". More precisely, if X is a set (mathematics), set, "almost all elements of X" means "all elements of X but those in a negligible set, negligible subset of X". The meaning o ...
real numbers are transcendental. The logarithm is an example of a
transcendental function. The
Gelfond–Schneider theorem asserts that logarithms usually take transcendental, i.e. "difficult" values.
Calculation

Logarithms are easy to compute in some cases, such as . In general, logarithms can be calculated using
power series or the
arithmetic–geometric mean, or be retrieved from a precalculated
logarithm table that provides a fixed precision.
Newton's method, an iterative method to solve equations approximately, can also be used to calculate the logarithm, because its inverse function, the exponential function, can be computed efficiently. Using look-up tables,
CORDIC-like methods can be used to compute logarithms by using only the operations of addition and
bit shifts. Moreover, the
binary logarithm algorithm calculates
recursively, based on repeated squarings of , taking advantage of the relation
Power series
Taylor series
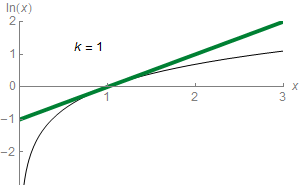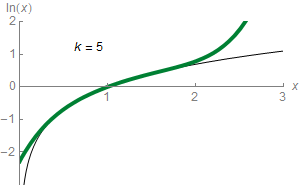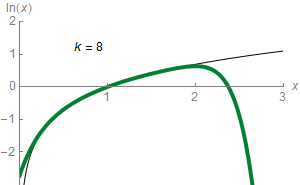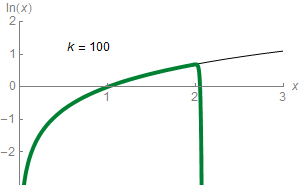
For any real number that satisfies , the following formula holds:
Equating the function to this infinite sum (
series) is shorthand for saying that the function can be approximated to a more and more accurate value by the following expressions (known as
partial sums):
For example, with the third approximation yields , which is about greater than , and the ninth approximation yields , which is only about greater. The th partial sum can approximate with arbitrary precision, provided the number of summands is large enough.
In elementary calculus, the series is said to
converge to the function , and the function is the
limit of the series. It is the
Taylor series of the
natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
at . The Taylor series of provides a particularly useful approximation to when is small, , since then
For example, with the first-order approximation gives , which is less than off the correct value .
Inverse hyperbolic tangent
Another series is based on the
inverse hyperbolic tangent function:
for any real number .
Using
sigma notation, this is also written as
This series can be derived from the above Taylor series. It converges quicker than the Taylor series, especially if is close to 1. For example, for , the first three terms of the second series approximate with an error of about . The quick convergence for close to 1 can be taken advantage of in the following way: given a low-accuracy approximation and putting
the logarithm of is:
The better the initial approximation is, the closer is to 1, so its logarithm can be calculated efficiently. can be calculated using the
exponential series, which converges quickly provided is not too large. Calculating the logarithm of larger can be reduced to smaller values of by writing , so that .
A closely related method can be used to compute the logarithm of integers. Putting
in the above series, it follows that:
If the logarithm of a large integer is known, then this series yields a fast converging series for , with a
rate of convergence of
.
Arithmetic–geometric mean approximation
The
arithmetic–geometric mean yields high-precision approximations of the
natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
. Sasaki and Kanada showed in 1982 that it was particularly fast for precisions between 400 and 1000 decimal places, while Taylor series methods were typically faster when less precision was needed. In their work is approximated to a precision of (or precise bits) by the following formula (due to
Carl Friedrich Gauss):
Here denotes the
arithmetic–geometric mean of and . It is obtained by repeatedly calculating the average (
arithmetic mean) and
(
geometric mean
In mathematics, the geometric mean is a mean or average which indicates a central tendency of a finite collection of positive real numbers by using the product of their values (as opposed to the arithmetic mean which uses their sum). The geometri ...
) of and then let those two numbers become the next and . The two numbers quickly converge to a common limit which is the value of . is chosen such that
to ensure the required precision. A larger makes the calculation take more steps (the initial and are farther apart so it takes more steps to converge) but gives more precision. The constants and can be calculated with quickly converging series.
Feynman's algorithm
While at
Los Alamos National Laboratory working on the
Manhattan Project,
Richard Feynman developed a bit-processing algorithm to compute the logarithm that is similar to long division and was later used in the
Connection Machine. The algorithm relies on the fact that every real number where can be represented as a product of distinct factors of the form . The algorithm sequentially builds that product , starting with and : if , then it changes to . It then increases
by one regardless. The algorithm stops when is large enough to give the desired accuracy. Because is the sum of the terms of the form corresponding to those for which the factor was included in the product , may be computed by simple addition, using a table of for all . Any base may be used for the logarithm table.
Applications

Logarithms have many applications inside and outside mathematics. Some of these occurrences are related to the notion of
scale invariance. For example, each chamber of the shell of a
nautilus is an approximate copy of the next one, scaled by a constant factor. This gives rise to a
logarithmic spiral.
Benford's law on the distribution of leading digits can also be explained by scale invariance. Logarithms are also linked to
self-similarity. For example, logarithms appear in the analysis of algorithms that solve a problem by dividing it into two similar smaller problems and patching their solutions. The dimensions of self-similar geometric shapes, that is, shapes whose parts resemble the overall picture are also based on logarithms.
Logarithmic scale
A logarithmic scale (or log scale) is a method used to display numerical data that spans a broad range of values, especially when there are significant differences among the magnitudes of the numbers involved.
Unlike a linear Scale (measurement) ...
s are useful for quantifying the relative change of a value as opposed to its absolute difference. Moreover, because the logarithmic function grows very slowly for large , logarithmic scales are used to compress large-scale scientific data. Logarithms also occur in numerous scientific formulas, such as the
Tsiolkovsky rocket equation, the
Fenske equation, or the
Nernst equation.
Logarithmic scale

Scientific quantities are often expressed as logarithms of other quantities, using a ''logarithmic scale''. For example, the
decibel is a
unit of measurement
A unit of measurement, or unit of measure, is a definite magnitude (mathematics), magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other qua ...
associated with
logarithmic-scale quantities. It is based on the common logarithm of
ratio
In mathematics, a ratio () shows how many times one number contains another. For example, if there are eight oranges and six lemons in a bowl of fruit, then the ratio of oranges to lemons is eight to six (that is, 8:6, which is equivalent to the ...
s—10 times the common logarithm of a
power ratio or 20 times the common logarithm of a
voltage ratio. It is used to quantify the attenuation or amplification of electrical signals, to describe power levels of sounds in
acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician ...
, and the
absorbance of light in the fields of
spectrometry and
optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of optical instruments, instruments that use or Photodetector, detect it. Optics usually describes t ...
. The
signal-to-noise ratio describing the amount of unwanted
noise in relation to a (meaningful)
signal is also measured in decibels. In a similar vein, the
peak signal-to-noise ratio is commonly used to assess the quality of sound and
image compression methods using the logarithm.
The strength of an earthquake is measured by taking the common logarithm of the energy emitted at the quake. This is used in the
moment magnitude scale
The moment magnitude scale (MMS; denoted explicitly with or Mwg, and generally implied with use of a single M for magnitude) is a measure of an earthquake's magnitude ("size" or strength) based on its seismic moment. was defined in a 1979 paper ...
or the
Richter magnitude scale. For example, a 5.0 earthquake releases 32 times and a 6.0 releases 1000 times the energy of a 4.0.
Apparent magnitude measures the brightness of stars logarithmically. In
chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
the negative of the decimal logarithm, the decimal , is indicated by the letter p.
For instance,
pH is the decimal cologarithm of the
activity of
hydronium ions (the form
hydrogen
Hydrogen is a chemical element; it has chemical symbol, symbol H and atomic number 1. It is the lightest and abundance of the chemical elements, most abundant chemical element in the universe, constituting about 75% of all baryon, normal matter ...
ions take in water). The activity of hydronium ions in neutral water is 10
−7 mol·L−1, hence a pH of 7. Vinegar typically has a pH of about 3. The difference of 4 corresponds to a ratio of 10
4 of the activity, that is, vinegar's hydronium ion activity is about .
Semilog (log–linear) graphs use the logarithmic scale concept for visualization: one axis, typically the vertical one, is scaled logarithmically. For example, the chart at the right compresses the steep increase from 1 million to 1 trillion to the same space (on the vertical axis) as the increase from 1 to 1 million. In such graphs,
exponential functions of the form appear as straight lines with
slope equal to the logarithm of .
Log-log graphs scale both axes logarithmically, which causes functions of the form to be depicted as straight lines with slope equal to the exponent . This is applied in visualizing and analyzing
power laws.
Psychology
Logarithms occur in several laws describing
human perception:
Hick's law proposes a logarithmic relation between the time individuals take to choose an alternative and the number of choices they have.
Fitts's law predicts that the time required to rapidly move to a target area is a logarithmic function of the ratio between the distance to a target and the size of the target. In
psychophysics, the
Weber–Fechner law proposes a logarithmic relationship between
stimulus and
sensation such as the actual vs. the perceived weight of an item a person is carrying. (This "law", however, is less realistic than more recent models, such as
Stevens's power law.)
Psychological studies found that individuals with little mathematics education tend to estimate quantities logarithmically, that is, they position a number on an unmarked line according to its logarithm, so that 10 is positioned as close to 100 as 100 is to 1000. Increasing education shifts this to a linear estimate (positioning 1000 10 times as far away) in some circumstances, while logarithms are used when the numbers to be plotted are difficult to plot linearly.
Probability theory and statistics

Logarithms arise in
probability theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expre ...
: the
law of large numbers dictates that, for a
fair coin, as the number of coin-tosses increases to infinity, the observed proportion of heads
approaches one-half. The fluctuations of this proportion about one-half are described by the
law of the iterated logarithm.
Logarithms also occur in
log-normal distributions. When the logarithm of a
random variable has a
normal distribution, the variable is said to have a log-normal distribution. Log-normal distributions are encountered in many fields, wherever a variable is formed as the product of many independent positive random variables, for example in the study of turbulence.
Logarithms are used for
maximum-likelihood estimation of parametric
statistical models. For such a model, the
likelihood function
A likelihood function (often simply called the likelihood) measures how well a statistical model explains observed data by calculating the probability of seeing that data under different parameter values of the model. It is constructed from the ...
depends on at least one
parameter that must be estimated. A maximum of the likelihood function occurs at the same parameter-value as a maximum of the logarithm of the likelihood (the "''log likelihood''"), because the logarithm is an increasing function. The log-likelihood is easier to maximize, especially for the multiplied likelihoods for
independent random variables.
Benford's law describes the occurrence of digits in many
data set
A data set (or dataset) is a collection of data. In the case of tabular data, a data set corresponds to one or more table (database), database tables, where every column (database), column of a table represents a particular Variable (computer sci ...
s, such as heights of buildings. According to Benford's law, the probability that the first decimal-digit of an item in the data sample is (from 1 to 9) equals , ''regardless'' of the unit of measurement. Thus, about 30% of the data can be expected to have 1 as first digit, 18% start with 2, etc. Auditors examine deviations from Benford's law to detect fraudulent accounting.
The
logarithm transformation is a type of
data transformation used to bring the empirical distribution closer to the assumed one.
Computational complexity
Analysis of algorithms is a branch of
computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
that studies the
performance
A performance is an act or process of staging or presenting a play, concert, or other form of entertainment. It is also defined as the action or process of carrying out or accomplishing an action, task, or function.
Performance has evolved glo ...
of
algorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
s (computer programs solving a certain problem).
[, pp. 1–2] Logarithms are valuable for describing algorithms that
divide a problem into smaller ones, and join the solutions of the subproblems.
For example, to find a number in a sorted list, the
binary search algorithm checks the middle entry and proceeds with the half before or after the middle entry if the number is still not found. This algorithm requires, on average, comparisons, where is the list's length. Similarly, the
merge sort algorithm sorts an unsorted list by dividing the list into halves and sorting these first before merging the results. Merge sort algorithms typically require a time
approximately proportional to . The base of the logarithm is not specified here, because the result only changes by a constant factor when another base is used. A constant factor is usually disregarded in the analysis of algorithms under the standard
uniform cost model.
A function is said to
grow logarithmically if is (exactly or approximately) proportional to the logarithm of . (Biological descriptions of organism growth, however, use this term for an exponential function.) For example, any
natural number
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ...
can be represented in
binary form
Binary form is a musical form in 2 related sections, both of which are usually repeated. Binary is also a structure used to choreograph dance. In music this is usually performed as A-A-B-B.
Binary form was popular during the Baroque music, Baro ...
in no more than
bits. In other words, the amount of
memory
Memory is the faculty of the mind by which data or information is encoded, stored, and retrieved when needed. It is the retention of information over time for the purpose of influencing future action. If past events could not be remembe ...
needed to store grows logarithmically with .
Entropy and chaos
 Entropy
Entropy is broadly a measure of the disorder of some system. In
statistical thermodynamics, the entropy of some physical system is defined as
The sum is over all possible states of the system in question, such as the positions of gas particles in a container. Moreover, is the probability that the state is attained and is the
Boltzmann constant. Similarly,
entropy in information theory measures the quantity of information. If a message recipient may expect any one of possible messages with equal likelihood, then the amount of information conveyed by any one such message is quantified as bits.
Lyapunov exponents use logarithms to gauge the degree of chaoticity of a
dynamical system. For example, for a particle moving on an oval billiard table, even small changes of the initial conditions result in very different paths of the particle. Such systems are
chaotic in a
deterministic way, because small measurement errors of the initial state predictably lead to largely different final states. At least one Lyapunov exponent of a deterministically chaotic system is positive.
Fractals

Logarithms occur in definitions of the
dimension of
fractal
In mathematics, a fractal is a Shape, geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scale ...
s. Fractals are geometric objects that are self-similar in the sense that small parts reproduce, at least roughly, the entire global structure. The
Sierpinski triangle (pictured) can be covered by three copies of itself, each having sides half the original length. This makes the
Hausdorff dimension of this structure . Another logarithm-based notion of dimension is obtained by
counting the number of boxes needed to cover the fractal in question.
Music
Logarithms are related to musical tones and
intervals. In
equal temperament
An equal temperament is a musical temperament or Musical tuning#Tuning systems, tuning system that approximates Just intonation, just intervals by dividing an octave (or other interval) into steps such that the ratio of the frequency, frequencie ...
tunings, the frequency ratio depends only on the interval between two tones, not on the specific frequency, or
pitch, of the individual tones. In the
12-tone equal temperament tuning common in modern Western music, each
octave (doubling of frequency) is broken into twelve equally spaced intervals called
semitones. For example, if the
note ''A'' has a frequency of 440
Hz then the note
''B-flat'' has a frequency of 466 Hz. The interval between ''A'' and ''B-flat'' is a
semitone, as is the one between ''B-flat'' and
''B'' (frequency 493 Hz). Accordingly, the frequency ratios agree:
Intervals between arbitrary pitches can be measured in octaves by taking the logarithm of the
frequency ratio, can be measured in equally tempered semitones by taking the logarithm ( times the logarithm), or can be measured in
cents, hundredths of a semitone, by taking the logarithm ( times the logarithm). The latter is used for finer encoding, as it is needed for finer measurements or non-equal temperaments.
Number theory
Natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
s are closely linked to
counting prime numbers (2, 3, 5, 7, 11, ...), an important topic in
number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
. For any
integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
, the quantity of
prime number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime ...
s less than or equal to is denoted . The
prime number theorem
In mathematics, the prime number theorem (PNT) describes the asymptotic analysis, asymptotic distribution of the prime numbers among the positive integers. It formalizes the intuitive idea that primes become less common as they become larger by p ...
asserts that is approximately given by
in the sense that the ratio of and that fraction approaches 1 when tends to infinity. As a consequence, the probability that a randomly chosen number between 1 and is prime is inversely proportionality (mathematics), proportional to the number of decimal digits of . A far better estimate of is given by the logarithmic integral function, offset logarithmic integral function , defined by
The Riemann hypothesis, one of the oldest open mathematical conjectures, can be stated in terms of comparing and . The Erdős–Kac theorem describing the number of distinct prime factors also involves the
natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
.
The logarithm of ''n''
factorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times ...
, , is given by
This can be used to obtain Stirling's formula, an approximation of for large .
Generalizations
Complex logarithm

All the complex numbers that solve the equation
are called ''complex logarithms'' of , when is (considered as) a complex number. A complex number is commonly represented as , where and are real numbers and is an imaginary unit, the square of which is −1. Such a number can be visualized by a point in the complex plane, as shown at the right. The polar form encodes a non-zero complex number by its absolute value, that is, the (positive, real) distance to the origin (mathematics), origin, and an angle between the real () axis'' '' and the line passing through both the origin and . This angle is called the Argument (complex analysis), argument of .
The absolute value of is given by
Using the geometrical interpretation of sine and cosine and their periodicity in , any complex number may be denoted as
for any integer number . Evidently the argument of is not uniquely specified: both and are valid arguments of for all integers , because adding radians or ''k''⋅360° to corresponds to "winding" around the origin counter-clock-wise by Turn (geometry), turns. The resulting complex number is always , as illustrated at the right for . One may select exactly one of the possible arguments of as the so-called ''principal argument'', denoted , with a capital , by requiring to belong to one, conveniently selected turn, e.g. or . These regions, where the argument of is uniquely determined are called principal branch, ''branches'' of the argument function.

Euler's formula connects the trigonometric functions sine and cosine to the complex exponential:
Using this formula, and again the periodicity, the following identities hold:
where is the unique real natural logarithm, denote the complex logarithms of , and is an arbitrary integer. Therefore, the complex logarithms of , which are all those complex values for which the power of equals , are the infinitely many values
for arbitrary integers .
Taking such that is within the defined interval for the principal arguments, then is called the ''principal value'' of the logarithm, denoted , again with a capital . The principal argument of any positive real number is 0; hence is a real number and equals the real (natural) logarithm. However, the above formulas for logarithms of products and powers Exponentiation#Failure of power and logarithm identities, do generalize to the principal value of the complex logarithm.
The illustration at the right depicts , confining the arguments of to the interval . This way the corresponding branch of the complex logarithm has discontinuities all along the negative real axis, which can be seen in the jump in the hue there. This discontinuity arises from jumping to the other boundary in the same branch, when crossing a boundary, i.e. not changing to the corresponding -value of the continuously neighboring branch. Such a locus is called a branch cut. Dropping the range restrictions on the argument makes the relations "argument of ", and consequently the "logarithm of ", multi-valued functions.
Inverses of other exponential functions
Exponentiation occurs in many areas of mathematics and its inverse function is often referred to as the logarithm. For example, the logarithm of a matrix is the (multi-valued) inverse function of the matrix exponential. Another example is the p-adic logarithm function, ''p''-adic logarithm, the inverse function of the p-adic exponential function, ''p''-adic exponential. Both are defined via Taylor series analogous to the real case. In the context of differential geometry, the exponential map (Riemannian geometry), exponential map maps the tangent space at a point of a differentiable manifold, manifold to a neighborhood (mathematics), neighborhood of that point. Its inverse is also called the logarithmic (or log) map.
In the context of finite groups exponentiation is given by repeatedly multiplying one group element with itself. The
discrete logarithm is the integer ' solving the equation
where is an element of the group. Carrying out the exponentiation can be done efficiently, but the discrete logarithm is believed to be very hard to calculate in some groups. This asymmetry has important applications in public key cryptography, such as for example in the Diffie–Hellman key exchange, a routine that allows secure exchanges of cryptography, cryptographic keys over unsecured information channels. Zech's logarithm is related to the discrete logarithm in the multiplicative group of non-zero elements of a finite field.
Further logarithm-like inverse functions include the ''double logarithm'' , the ''super-logarithm, super- or hyper-4-logarithm'' (a slight variation of which is called iterated logarithm in computer science), the Lambert W function, and the logit. They are the inverse functions of the double exponential function, tetration, of , and of the logistic function, respectively.
Related concepts
From the perspective of group theory, the identity expresses a group isomorphism between positive real number, reals under multiplication and reals under addition. Logarithmic functions are the only continuous isomorphisms between these groups. By means of that isomorphism, the Haar measure (Lebesgue measure) on the reals corresponds to the Haar measure on the positive reals. The non-negative reals not only have a multiplication, but also have addition, and form a semiring, called the probability semiring; this is in fact a semifield. The logarithm then takes multiplication to addition (log multiplication), and takes addition to log addition (LogSumExp), giving an isomorphism of semirings between the probability semiring and the log semiring.
logarithmic form, Logarithmic one-forms appear in complex analysis and algebraic geometry as differential forms with logarithmic Pole (complex analysis), poles.
The polylogarithm is the function defined by
It is related to the
natural logarithm
The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ...
by . Moreover, equals the Riemann zeta function .
See also
* Decimal exponent (dex)
* Exponential function
* Index of logarithm articles
Notes
References
External links
*
*
*
*
*
Khan Academy: Logarithms, free online micro lectures*
*
*
*
{{Authority control
Logarithms,
Elementary special functions
Scottish inventions
Additive functions
 In
In 
 Logarithms are easy to compute in some cases, such as . In general, logarithms can be calculated using power series or the arithmetic–geometric mean, or be retrieved from a precalculated logarithm table that provides a fixed precision. Newton's method, an iterative method to solve equations approximately, can also be used to calculate the logarithm, because its inverse function, the exponential function, can be computed efficiently. Using look-up tables, CORDIC-like methods can be used to compute logarithms by using only the operations of addition and bit shifts. Moreover, the binary logarithm algorithm calculates recursively, based on repeated squarings of , taking advantage of the relation
Logarithms are easy to compute in some cases, such as . In general, logarithms can be calculated using power series or the arithmetic–geometric mean, or be retrieved from a precalculated logarithm table that provides a fixed precision. Newton's method, an iterative method to solve equations approximately, can also be used to calculate the logarithm, because its inverse function, the exponential function, can be computed efficiently. Using look-up tables, CORDIC-like methods can be used to compute logarithms by using only the operations of addition and bit shifts. Moreover, the binary logarithm algorithm calculates recursively, based on repeated squarings of , taking advantage of the relation
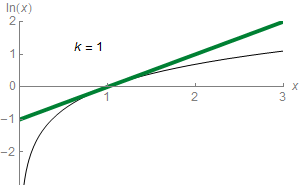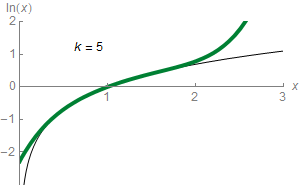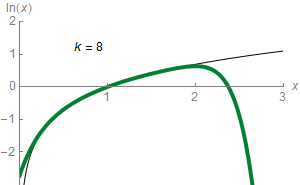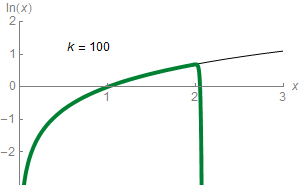 For any real number that satisfies , the following formula holds:
Equating the function to this infinite sum ( series) is shorthand for saying that the function can be approximated to a more and more accurate value by the following expressions (known as partial sums):
For example, with the third approximation yields , which is about greater than , and the ninth approximation yields , which is only about greater. The th partial sum can approximate with arbitrary precision, provided the number of summands is large enough.
In elementary calculus, the series is said to converge to the function , and the function is the limit of the series. It is the Taylor series of the
For any real number that satisfies , the following formula holds:
Equating the function to this infinite sum ( series) is shorthand for saying that the function can be approximated to a more and more accurate value by the following expressions (known as partial sums):
For example, with the third approximation yields , which is about greater than , and the ninth approximation yields , which is only about greater. The th partial sum can approximate with arbitrary precision, provided the number of summands is large enough.
In elementary calculus, the series is said to converge to the function , and the function is the limit of the series. It is the Taylor series of the  Logarithms have many applications inside and outside mathematics. Some of these occurrences are related to the notion of scale invariance. For example, each chamber of the shell of a nautilus is an approximate copy of the next one, scaled by a constant factor. This gives rise to a logarithmic spiral. Benford's law on the distribution of leading digits can also be explained by scale invariance. Logarithms are also linked to self-similarity. For example, logarithms appear in the analysis of algorithms that solve a problem by dividing it into two similar smaller problems and patching their solutions. The dimensions of self-similar geometric shapes, that is, shapes whose parts resemble the overall picture are also based on logarithms.
Logarithms have many applications inside and outside mathematics. Some of these occurrences are related to the notion of scale invariance. For example, each chamber of the shell of a nautilus is an approximate copy of the next one, scaled by a constant factor. This gives rise to a logarithmic spiral. Benford's law on the distribution of leading digits can also be explained by scale invariance. Logarithms are also linked to self-similarity. For example, logarithms appear in the analysis of algorithms that solve a problem by dividing it into two similar smaller problems and patching their solutions. The dimensions of self-similar geometric shapes, that is, shapes whose parts resemble the overall picture are also based on logarithms.