|
Fortune's Algorithm
Fortune's algorithm is a sweep line algorithm for generating a Voronoi diagram from a set of points in a plane using O(''n'' log ''n'') time and O(''n'') space. Section 7.2: Computing the Voronoi Diagram: pp.151–160. It was originally published by Steven Fortune in 1986 in his paper "A sweepline algorithm for Voronoi diagrams." Algorithm description The algorithm maintains both a sweep line and a ''beach line'', which both move through the plane as the algorithm progresses. The sweep line is a straight line, which we may by convention assume to be vertical and moving left to right across the plane. At any time during the algorithm, the input points left of the sweep line will have been incorporated into the Voronoi diagram, while the points right of the sweep line will not have been considered yet. The beach line is not a straight line, but a complicated, piecewise curve to the left of the sweep line, composed of pieces of parabolas; it divides the portion of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directrix (conic Section)
A conic section, conic or a quadratic curve is a curve obtained from a Conical surface, cone's surface intersecting a plane (mathematics), plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. The Greek mathematics, ancient Greek mathematicians studied conic sections, culminating around 200 BC with Apollonius of Perga's systematic work on their properties. The conic sections in the Euclidean plane have various distinguishing properties, many of which can be used as alternative definitions. One such property defines a non-circular conic to be the set (mathematics), set of those points whose distances to some particular point, called a ''Focus (geometry), focus'', and some particular line, called a ''directrix'', are in a fixed ratio, called the ''Eccentricity (mathematics), eccentricity''. The type of conic is determined by the value of the ec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Diagram
In computational geometry, a power diagram, also called a Laguerre–Voronoi diagram, Dirichlet cell complex, radical Voronoi tesselation or a sectional Dirichlet tesselation, is a partition of the Euclidean plane into polygonal cells defined from a set of circles. The cell for a given circle ''C'' consists of all the points for which the Power of a point, power distance to ''C'' is smaller than the power distance to the other circles. The power diagram is a form of generalized Voronoi diagram, and coincides with the Voronoi diagram of the circle centers in the case that all the circles have equal radii.... Definition If ''C'' is a circle and ''P'' is a point outside ''C'', then the Power of a point, power of ''P'' with respect to ''C'' is the square of the length of a line segment from ''P'' to a point ''T'' of tangency with ''C''. Equivalently, if ''P'' has distance ''d'' from the center of the circle, and the circle has radius ''r'', then (by the Pythagorean theorem) the power ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
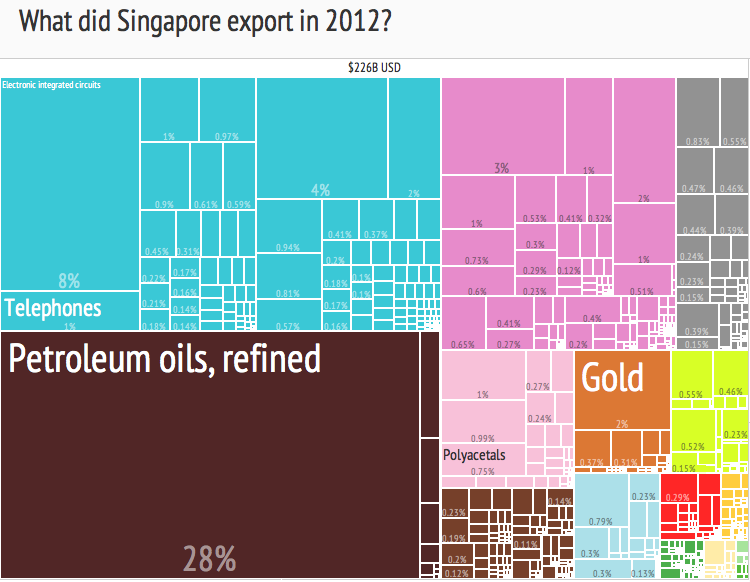
Treemap
In information visualization and computing, treemapping is a method for displaying hierarchical data using Nesting (computing), nested figures, usually rectangles. Treemaps display hierarchical (Tree (data structure), tree-structured) data as a set of nested rectangles. Each branch of the tree is given a rectangle, which is then tiled with smaller rectangles representing sub-branches. A leaf node's rectangle has an area proportional to a specified Dimension (metadata), dimension of the data. Often the leaf nodes are colored to show a separate dimension of the data. When the color and size dimensions are correlated in some way with the tree structure, one can often easily see patterns that would be difficult to spot in other ways, such as whether a certain color is particularly prevalent. A second advantage of treemaps is that, by construction, they make efficient use of space. As a result, they can legibly display thousands of items on the screen simultaneously. Tiling algorith ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pseudocode
In computer science, pseudocode is a description of the steps in an algorithm using a mix of conventions of programming languages (like assignment operator, conditional operator, loop) with informal, usually self-explanatory, notation of actions and conditions. Although pseudocode shares features with regular programming languages, it is intended for human reading rather than machine control. Pseudocode typically omits details that are essential for machine implementation of the algorithm, meaning that pseudocode can only be verified by hand. The programming language is augmented with natural language description details, where convenient, or with compact mathematical notation. The reasons for using pseudocode are that it is easier for people to understand than conventional programming language code and that it is an efficient and environment-independent description of the key principles of an algorithm. It is commonly used in textbooks and scientific publications to document ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Priority Queue
In computer science, a priority queue is an abstract data type similar to a regular queue (abstract data type), queue or stack (abstract data type), stack abstract data type. In a priority queue, each element has an associated ''priority'', which determines its order of service. Priority queue serves highest priority items first. Priority values have to be instances of an ordered data type, and higher priority can be given either to the lesser or to the greater values with respect to the given order relation. For example, in Java (programming language), Java standard library, ''PriorityQueues the least elements with respect to the order have the highest priority. This implementation detail is without much practical significance, since passing to the converse relation, opposite order relation turns the least values into the greatest, and vice versa. While priority queues are often implemented using Heap (data structure) , heaps, they are conceptually distinct. A priority queue can ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Search Tree
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a Rooted tree, rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is Time complexity#Linear time, linear with respect to the height of the tree. Binary search trees allow Binary search algorithm, binary search for fast lookup, addition, and removal of data items. Since the nodes in a BST are laid out so that each comparison skips about half of the remaining tree, the lookup performance is proportional to that of binary logarithm. BSTs were devised in the 1960s for the problem of efficient storage of labeled data and are attributed to Conway Berners-Lee and David_Wheeler_(computer_scientist), David Wheeler. The performance of a binary search tree is dependent on the order of insertion of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactly the same curves. One description of a parabola involves a Point (geometry), point (the Focus (geometry), focus) and a Line (geometry), line (the Directrix (conic section), directrix). The focus does not lie on the directrix. The parabola is the locus (mathematics), locus of points in that plane that are equidistant from the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane (geometry), plane Parallel (geometry), parallel to another plane that is tangential to the conical surface. The graph of a function, graph of a quadratic function y=ax^2+bx+ c (with a\neq 0 ) is a parabola with its axis parallel to the -axis. Conversely, every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sweep Line Algorithm
In computational geometry, a sweep line algorithm or plane sweep algorithm is an algorithmic paradigm that uses a conceptual ''sweep line'' or ''sweep surface'' to solve various problems in Euclidean space. It is one of the critical techniques in computational geometry. The idea behind algorithms of this type is to imagine that a line (often a vertical line) is swept or moved across the plane, stopping at some points. Geometric operations are restricted to geometric objects that either intersect or are in the immediate vicinity of the sweep line whenever it stops, and the complete solution is available once the line has passed over all objects. Applications An application of the approach had led to a breakthrough in the Analysis of algorithms, computational complexity of geometric algorithms when Michael Ian Shamos, Shamos and Hoey presented algorithms for line segment intersection in the plane in 1976. In particular, they described how a combination of the scanline approach with ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Piecewise
In mathematics, a piecewise function (also called a piecewise-defined function, a hybrid function, or a function defined by cases) is a function whose domain is partitioned into several intervals ("subdomains") on which the function may be defined differently. Piecewise definition is actually a way of specifying the function, rather than a characteristic of the resulting function itself, as every function whose domain contains at least two points can be rewritten as a piecewise function. The first three paragraphs of this article only deal with this first meaning of "piecewise". Terms like piecewise linear, piecewise smooth, piecewise continuous, and others are also very common. The meaning of a function being piecewise P, for a property P is roughly that the domain of the function can be partitioned into pieces on which the property P holds, but is used slightly differently by different authors. Unlike the first meaning, this is a property of the function itself and not on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sweep Line
In computational geometry, a sweep line algorithm or plane sweep algorithm is an algorithmic paradigm that uses a conceptual ''sweep line'' or ''sweep surface'' to solve various problems in Euclidean space. It is one of the critical techniques in computational geometry. The idea behind algorithms of this type is to imagine that a line (often a vertical line) is swept or moved across the plane, stopping at some points. Geometric operations are restricted to geometric objects that either intersect or are in the immediate vicinity of the sweep line whenever it stops, and the complete solution is available once the line has passed over all objects. Applications An application of the approach had led to a breakthrough in the computational complexity of geometric algorithms when Shamos and Hoey presented algorithms for line segment intersection in the plane in 1976. In particular, they described how a combination of the scanline approach with efficient data structures (self-balancing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |