Treemap on:
[Wikipedia]
[Google]
[Amazon]
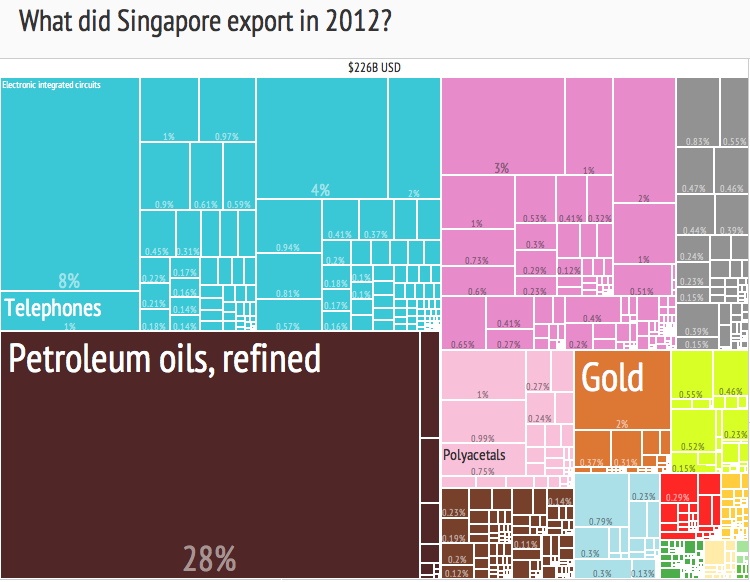 In
In
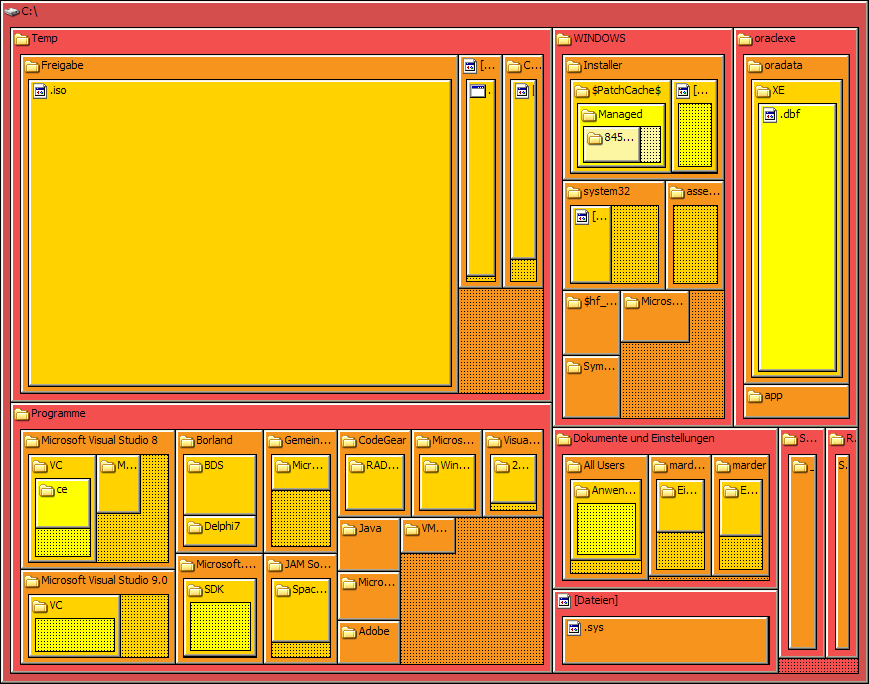 Area-based visualizations have existed for decades. For example,
Area-based visualizations have existed for decades. For example,
Treemap Art Project
produced exhibit for the National Academies in Washington, DC
"Discovering Business Intelligence Using Treemap Visualizations"
Comprehensive survey and bibliography
of Tree Visualization techniques *
History of Treemaps
by Ben Shneiderman.
Hypermedia exploration with interactive dynamic maps
Paper by Zizi and Beaudouin-Lafon introducing the squarified treemap layout algorithm (named "improved treemap layout" at the time).
description
Live interactive treemap based on crowd-sourced discounted deals
from '' Flytail Group''
Treemap sample in English
from '' The Hive Group''
Several treemap examples
made with Macrofocus TreeMap
Visualizations using dynamic treemaps
an
by drasticdata {{Visualization User interface techniques Infographics Statistical charts and diagrams Trees (data structures) Visualization (graphics) Rectangular subdivisions
 In
In information visualization
Data and information visualization (data viz/vis or info viz/vis) is the practice of designing and creating Graphics, graphic or visual Representation (arts), representations of a large amount of complex quantitative and qualitative data and i ...
and computing
Computing is any goal-oriented activity requiring, benefiting from, or creating computer, computing machinery. It includes the study and experimentation of algorithmic processes, and the development of both computer hardware, hardware and softw ...
, treemapping is a method for displaying hierarchical
A hierarchy (from Greek: , from , 'president of sacred rites') is an arrangement of items (objects, names, values, categories, etc.) that are represented as being "above", "below", or "at the same level as" one another. Hierarchy is an importan ...
data using nested figures, usually rectangles.
Treemaps display hierarchical ( tree-structured) data as a set of nested rectangles. Each branch of the tree is given a rectangle, which is then tiled with smaller rectangles representing sub-branches. A leaf node's rectangle has an area proportional to a specified dimension of the data. Often the leaf nodes are colored to show a separate dimension of the data.
When the color and size dimensions are correlated in some way with the tree structure, one can often easily see patterns that would be difficult to spot in other ways, such as whether a certain color is particularly prevalent. A second advantage of treemaps is that, by construction, they make efficient use of space. As a result, they can legibly display thousands of items on the screen simultaneously.
Tiling algorithms
To create a treemap, one must define a tilingalgorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
, that is, a way to divide a region into sub-regions of specified areas. Ideally, a treemap algorithm would create regions that satisfy the following criteria:
# A small aspect ratio
The aspect ratio of a geometry, geometric shape is the ratio of its sizes in different dimensions. For example, the aspect ratio of a rectangle is the ratio of its longer side to its shorter side—the ratio of width to height, when the rectangl ...
—ideally close to one. Regions with a small aspect ratio (i.e., fat objects) are easier to perceive.
# Preserve some sense of the ordering in the input data (ordered).
# Change to reflect changes in the underlying data (high stability).
These properties have an inverse relationship. As the aspect ratio is optimized, the order of placement becomes less predictable. As the order becomes more stable, the aspect ratio is degraded.
Rectangular treemaps
To date, fifteen primary rectangular treemap algorithms have been developed:Convex treemaps
Rectangular treemaps have the disadvantage that their aspect ratio might be arbitrarily high in the worst case. As a simple example, if the tree root has only two children, one with weight and one with weight , then the aspect ratio of the smaller child will be , which can be arbitrarily high. To cope with this problem, several algorithms have been proposed that use regions that are generalconvex polygon
In geometry, a convex polygon is a polygon that is the boundary of a convex set. This means that the line segment between two points of the polygon is contained in the union of the interior and the boundary of the polygon. In particular, it is ...
s, not necessarily rectangular.
Convex treemaps were developed in several steps, each step improved the upper bound on the aspect ratio. The bounds are given as a function of - the total number of nodes in the tree, and - the total depth of the tree.
#Onak and Sidiropoulos proved an upper bound of .
#De-Berg and Onak and Sidiropoulos improve the upper bound to , and prove a lower bound of .
#De-Berg and Speckmann and van-der-Weele. Conference version: improve the upper bound to , matching the theoretical lower bound. (For the special case where the depth is 1, they present an algorithm that uses only four classes of 45-degree-polygons (rectangles, right-angled triangles, right-angled trapezoids and 45-degree pentagons), and guarantees an aspect ratio of at most 34/7.)
The latter two algorithms operate in two steps (greatly simplified for clarity):
# The original tree is converted to a binary tree: each node with more than two children is replaced by a sub-tree in which each node has exactly two children.
# Each region representing a node (starting from the root) is divided to two, using a line that keeps the angles between edges as large as possible. It is possible to prove that, if all edges of a convex polygon are separated by an angle of at least , then its aspect ratio is . It is possible to ensure that, in a tree of depth , the angle is divided by a factor of at most , hence the aspect ratio guarantee.
Orthoconvex treemaps
In convex treemaps, the aspect ratio cannot be constant - it grows with the depth of the tree. To attain a constant aspect-ratio, Orthoconvex treemaps can be used. There, all regions are orthoconvexrectilinear polygon
A rectilinear polygon is a polygon all of whose sides meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons.
In many cases another definition is p ...
s with aspect ratio at most 64; and the leaves are either rectangles with aspect ratio at most 8, or L-shapes or S-shapes with aspect ratio at most 32.
For the special case where the depth is 1, they present an algorithm that uses only rectangles and L-shapes, and the aspect ratio is at most ; the internal nodes use only rectangles with aspect ratio at most .
Other treemaps
;Voronoi Treemaps:. based onVoronoi diagram
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. It can be classified also as a tessellation. In the simplest case, these objects are just finitely many points in the plane (calle ...
calculations. The algorithm is iterative and does not give any upper bound on the aspect ratio.
;Jigsaw Treemaps.: based on the geometry of space-filling curves. They assume that the weights are integers and that their sum is a square number. The regions of the map are rectilinear polygon
A rectilinear polygon is a polygon all of whose sides meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons.
In many cases another definition is p ...
s and highly non-ortho-convex. Their aspect ratio is guaranteed to be at most 4.
;GosperMaps:. based on the geometry of Gosper curves. It is ordered and stable, but has a very high aspect ratio.
History
 Area-based visualizations have existed for decades. For example,
Area-based visualizations have existed for decades. For example, mosaic plot
A mosaic plot, Marimekko chart, Mekko chart, or sometimes percent stacked bar plot, is a graphical visualization of data from two or more qualitative variables. It is the multidimensional extension of spineplots, which graphically display the same ...
s (also known as Marimekko diagrams) use rectangular tilings to show joint distributions (i.e., most commonly they are essentially stacked column plots where the columns are of different widths). The main distinguishing feature of a treemap, however, is the recursive construction that allows it to be extended to hierarchical data with any number of levels. This idea was invented by professor Ben Shneiderman
Ben Shneiderman (born August 21, 1947) is an American computer scientist, a Distinguished University Professor in the University of Maryland Department of Computer Science, which is part of the University of Maryland College of Computer, Mathem ...
at the University of Maryland Human – Computer Interaction Lab in the early 1990s.
Shneiderman and his collaborators then deepened the idea by introducing a variety of interactive techniques for filtering and adjusting treemaps.
These early treemaps all used the simple "slice-and-dice" tiling algorithm. Despite many desirable properties (it is stable, preserves ordering, and is easy to implement), the slice-and-dice method often produces tilings with many long, skinny rectangles. In 1994 Mountaz Hascoet and Michel Beaudouin-Lafon
Michel Beaudouin-Lafon (born 20 July 1961) is a French computer scientist working in the field of human–computer interaction. He received his PhD from the Paris-Sud 11 University (which is now Paris-Saclay University) in 1985. He is currently ...
invented a "squarifying" algorithm, later popularized by Jarke van Wijk
Jarke J. (Jack) van Wijk (born 1959) is a Dutch computer scientist, a professor in the Department of Mathematics and Computer Science at the Eindhoven University of Technology, and an expert in information visualization.
Biography
Van Wijk receive ...
, that created tilings whose rectangles were closer to square. In 1999 Martin Wattenberg used a variation of the "squarifying" algorithm that he called "pivot and slice" to create the first Web-based treemap, the SmartMoney Map of the Market, which displayed data on hundreds of companies in the U.S. stock market. Following its launch, treemaps enjoyed a surge of interest, particularly in financial contexts.
A third wave of treemap innovation came around 2004, after Marcos Weskamp
Marcos may refer to:
People with the given name ''Marcos''
*Marcos (given name)
* Marcos family
Sports
;Surnamed
* Dayton Marcos, Negro league baseball team from Dayton, Ohio (early twentieth-century)
* Dimitris Markos, Greek footballer
* Nél ...
created the Newsmap, a treemap that displayed news headlines. This example of a non-analytical treemap inspired many imitators, and introduced treemaps to a new, broad audience. In recent years, treemaps have made their way into the mainstream media, including usage by the New York Times.
The Treemap Art Project produced 12 framed images for the National Academies (United States)
The National Academies of Sciences, Engineering, and Medicine (NASEM), also known as the National Academies, is a Congressional charter, congressionally chartered organization that serves as the collective scientific national academy of the Uni ...
, shown at the Every AlgoRiThm has ART in It exhibit in Washington, DC and another set for the collection of Museum of Modern Art
The Museum of Modern Art (MoMA) is an art museum located in Midtown Manhattan, New York City, on 53rd Street (Manhattan), 53rd Street between Fifth Avenue, Fifth and Sixth Avenues. MoMA's collection spans the late 19th century to the present, a ...
in New York.
See also
*Disk space analyzer
A disk utility is a utility program that allows a user to perform various functions on a computer disk, such as disk partitioning and logical volume management, as well as multiple smaller tasks such as changing drive letters and other mount ...
* Data and information visualization
Data and information visualization (data viz/vis or info viz/vis) is the practice of designing and creating graphic or visual representations of a large amount of complex quantitative and qualitative data and information with the help of stat ...
* Marimekko Chart, a similar concept with one level of explicit hierarchy.
References
External links
Treemap Art Project
produced exhibit for the National Academies in Washington, DC
"Discovering Business Intelligence Using Treemap Visualizations"
Ben Shneiderman
Ben Shneiderman (born August 21, 1947) is an American computer scientist, a Distinguished University Professor in the University of Maryland Department of Computer Science, which is part of the University of Maryland College of Computer, Mathem ...
, April 11, 2006
Comprehensive survey and bibliography
of Tree Visualization techniques *
History of Treemaps
by Ben Shneiderman.
Hypermedia exploration with interactive dynamic maps
Paper by Zizi and Beaudouin-Lafon introducing the squarified treemap layout algorithm (named "improved treemap layout" at the time).
description
Live interactive treemap based on crowd-sourced discounted deals
from '' Flytail Group''
Treemap sample in English
from '' The Hive Group''
Several treemap examples
made with Macrofocus TreeMap
Visualizations using dynamic treemaps
an
by drasticdata {{Visualization User interface techniques Infographics Statistical charts and diagrams Trees (data structures) Visualization (graphics) Rectangular subdivisions