|
Dvoretzky–Kiefer–Wolfowitz Inequality
In the theory of probability Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and ... and statistics, the Dvoretzky–Kiefer–Wolfowitz–Massart inequality (DKW inequality) bounds how close an empirical distribution function, empirically determined distribution function will be to the cumulative distribution function, distribution function from which the empirical samples are drawn. It is named after Aryeh Dvoretzky, Jack Kiefer (mathematician), Jack Kiefer, and Jacob Wolfowitz, who in 1956 proved the inequality : \Pr\Bigl(\sup_ , F_n(x) - F(x), > \varepsilon \Bigr) \le Ce^\qquad \text\varepsilon>0. with an unspecified multiplicative constant ''C'' in front of the exponent on the right-hand side. In 1990, Pascal Massart proved the inequality with the sharp constant ''C'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
DKW Bounds
DKW (''Dampf-Kraft-Wagen'', en, "steam-powered car", also ''Deutsche Kinder-Wagen'' en, "German children's car". ''Das-Kleine-Wunder'', en, "the little wonder" or ''Des-Knaben-Wunsch'', en, "the boy's wish"- from when the company built toy two-stroke engines) was a German car- and motorcycle-marque. DKW was one of the four companies that formed Auto Union in 1932 and thus became an ancestor of the modern-day Audi company. In 1916, Danish engineer Jørgen Skafte Rasmussen founded a factory in Zschopau, Saxony, Germany, to produce steam fittings. That year he attempted to produce a steam-driven car, called the DKW.Odin, L.C. ''World in Motion 1939 – The whole of the year's automobile production''. Belvedere Publishing, 2015. ASIN: B00ZLN91ZG. Although unsuccessful, he made a two-stroke toy engine in 1919, called ''Des Knaben Wunsch'' – "the boy's wish". He put a slightly modified version of this engine into a motorcycle and called it ''Das Kleine Wunder'' – "the littl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Random Variable
A random variable (also called random quantity, aleatory variable, or stochastic variable) is a mathematical formalization of a quantity or object which depends on random events. It is a mapping or a function from possible outcomes (e.g., the possible upper sides of a flipped coin such as heads H and tails T) in a sample space (e.g., the set \) to a measurable space, often the real numbers (e.g., \ in which 1 corresponding to H and -1 corresponding to T). Informally, randomness typically represents some fundamental element of chance, such as in the roll of a dice; it may also represent uncertainty, such as measurement error. However, the interpretation of probability is philosophically complicated, and even in specific cases is not always straightforward. The purely mathematical analysis of random variables is independent of such interpretational difficulties, and can be based upon a rigorous axiomatic setup. In the formal mathematical language of measure theory, a rando ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Asymptotic Theory (statistics)
In statistics, asymptotic theory, or large sample theory, is a framework for assessing properties of estimators and statistical tests. Within this framework, it is often assumed that the sample size may grow indefinitely; the properties of estimators and tests are then evaluated under the limit of . In practice, a limit evaluation is considered to be approximately valid for large finite sample sizes too.Höpfner, R. (2014), Asymptotic Statistics, Walter de Gruyter. 286 pag. , Overview Most statistical problems begin with a dataset of size . The asymptotic theory proceeds by assuming that it is possible (in principle) to keep collecting additional data, thus that the sample size grows infinitely, i.e. . Under the assumption, many results can be obtained that are unavailable for samples of finite size. An example is the weak law of large numbers. The law states that for a sequence of independent and identically distributed (IID) random variables , if one value is drawn from each ra ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Concentration Inequality
In probability theory, concentration inequalities provide bounds on how a random variable deviates from some value (typically, its expected value). The law of large numbers of classical probability theory states that sums of independent random variables are, under very mild conditions, close to their expectation with a large probability. Such sums are the most basic examples of random variables concentrated around their mean. Recent results show that such behavior is shared by other functions of independent random variables. Concentration inequalities can be sorted according to how much information about the random variable is needed in order to use them. Markov's inequality Let X be a random variable that is non-negative (almost surely). Then, for every constant a > 0, : \Pr(X \geq a) \leq \frac. Note the following extension to Markov's inequality: if \Phi is a strictly increasing and non-negative function, then :\Pr(X \geq a) = \Pr(\Phi (X) \geq \Phi (a)) \leq \frac. Cheb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov%E2%80%93Smirnov Test
In statistics, the Kolmogorov–Smirnov test (K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section 2.2), one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). In essence, the test answers the question "What is the probability that this collection of samples could have been drawn from that probability distribution?" or, in the second case, "What is the probability that these two sets of samples were drawn from the same (but unknown) probability distribution?". It is named after Andrey Kolmogorov and Nikolai Smirnov. The Kolmogorov–Smirnov statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confidence And Prediction Bands
A confidence band is used in statistical analysis to represent the uncertainty in an estimate of a curve or function based on limited or noisy data. Similarly, a prediction band is used to represent the uncertainty about the value of a new data-point on the curve, but subject to noise. Confidence and prediction bands are often used as part of the graphical presentation of results of a regression analysis. Confidence bands are closely related to confidence intervals, which represent the uncertainty in an estimate of a single numerical value. "As confidence intervals, by construction, only refer to a single point, they are narrower (at this point) than a confidence band which is supposed to hold simultaneously at many points." Pointwise and simultaneous confidence bands Suppose our aim is to estimate a function ''f''(''x''). For example, ''f''(''x'') might be the proportion of people of a particular age ''x'' who support a given candidate in an election. If ''x'' is measured at t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elsevier
Elsevier () is a Dutch academic publishing company specializing in scientific, technical, and medical content. Its products include journals such as '' The Lancet'', '' Cell'', the ScienceDirect collection of electronic journals, '' Trends'', the '' Current Opinion'' series, the online citation database Scopus, the SciVal tool for measuring research performance, the ClinicalKey search engine for clinicians, and the ClinicalPath evidence-based cancer care service. Elsevier's products and services also include digital tools for data management, instruction, research analytics and assessment. Elsevier is part of the RELX Group (known until 2015 as Reed Elsevier), a publicly traded company. According to RELX reports, in 2021 Elsevier published more than 600,000 articles annually in over 2,700 journals; as of 2018 its archives contained over 17 million documents and 40,000 e-books, with over one billion annual downloads. Researchers have criticized Elsevier for its high profit ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
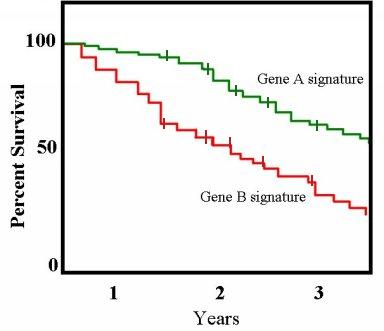
Kaplan–Meier Estimator
The Kaplan–Meier estimator, also known as the product limit estimator, is a non-parametric statistic used to estimate the survival function from lifetime data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In other fields, Kaplan–Meier estimators may be used to measure the length of time people remain unemployed after a job loss, the time-to-failure of machine parts, or how long fleshy fruits remain on plants before they are removed by frugivores. The estimator is named after Edward L. Kaplan and Paul Meier, who each submitted similar manuscripts to the ''Journal of the American Statistical Association''. The journal editor, John Tukey, convinced them to combine their work into one paper, which has been cited almost 61,000 times since its publication in 1958. The estimator of the survival function S(t) (the probability that life is longer than t) is given by: : \widehat S(t) = \prod\limits_ \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of symmetric probability distributions. The distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, ''a'' and ''b'', which are the minimum and maximum values. The interval can either be closed (e.g. , b or open (e.g. (a, b)). Therefore, the distribution is often abbreviated ''U'' (''a'', ''b''), where U stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable ''X'' under no constraint other than that it is contained in the distribution's support. Definitions Probability density function The probability density function of the continuous uniform distribution is: : f(x)=\be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kolmogorov–Smirnov Test
In statistics, the Kolmogorov–Smirnov test (K–S test or KS test) is a nonparametric test of the equality of continuous (or discontinuous, see Section 2.2), one-dimensional probability distributions that can be used to compare a sample with a reference probability distribution (one-sample K–S test), or to compare two samples (two-sample K–S test). In essence, the test answers the question "What is the probability that this collection of samples could have been drawn from that probability distribution?" or, in the second case, "What is the probability that these two sets of samples were drawn from the same (but unknown) probability distribution?". It is named after Andrey Kolmogorov and Nikolai Smirnov. The Kolmogorov–Smirnov statistic quantifies a distance between the empirical distribution function of the sample and the cumulative distribution function of the reference distribution, or between the empirical distribution functions of two samples. The null dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rate Of Convergence
In numerical analysis, the order of convergence and the rate of convergence of a convergent sequence are quantities that represent how quickly the sequence approaches its limit. A sequence (x_n) that converges to x^* is said to have ''order of convergence'' q \geq 1 and ''rate of convergence'' \mu if : \lim _ \frac=\mu. The rate of convergence \mu is also called the ''asymptotic error constant''. Note that this terminology is not standardized and some authors will use ''rate'' where this article uses ''order'' (e.g., ). In practice, the rate and order of convergence provide useful insights when using iterative methods for calculating numerical approximations. If the order of convergence is higher, then typically fewer iterations are necessary to yield a useful approximation. Strictly speaking, however, the asymptotic behavior of a sequence does not give conclusive information about any finite part of the sequence. Similar concepts are used for discretization methods. The solutio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glivenko–Cantelli Theorem
In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the Fundamental Theorem of Statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, determines the asymptotic behaviour of the empirical distribution function as the number of independent and identically distributed observations grows. The uniform convergence of more general empirical measures becomes an important property of the Glivenko–Cantelli classes of functions or sets. The Glivenko–Cantelli classes arise in Vapnik–Chervonenkis theory, with applications to machine learning. Applications can be found in econometrics making use of M-estimators. Statement Assume that X_1,X_2,\dots are independent and identically distributed random variables in \mathbb with common cumulative distribution function F(x). The ''empirical distribution function'' for X_1,\dots,X_n is defined by :F_n(x)=\frac\sum_^n I_(x) = \frac\left, \left\\ where I_C is the indicator fun ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |