|
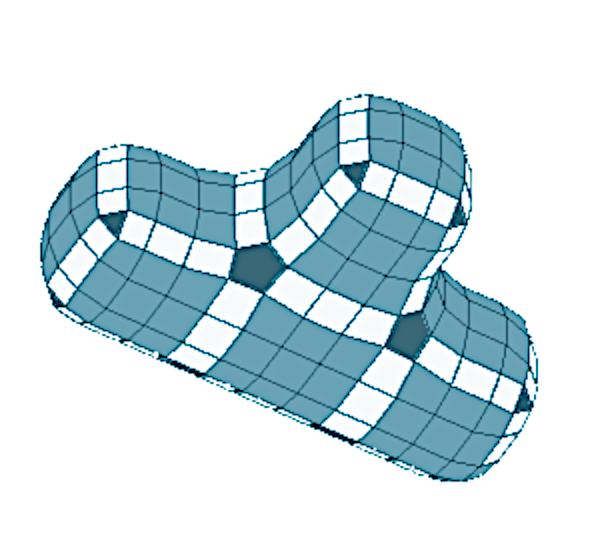
Doo–Sabin Subdivision Surface
In 3D computer graphics, a Doo–Sabin subdivision surface is a type of subdivision surface based on a generalization of '' bi-quadratic'' uniform B-splines, whereas Catmull-Clark was based on generalized '' bi-cubic'' uniform B-splines. The subdivision refinement algorithm was developed in 1978 by Daniel Doo and Malcolm Sabin.D. Doo: ''A subdivision algorithm for smoothing down irregularly shaped polyhedrons'', Proceedings on Interactive Techniques in Computer Aided Design, pp. 157 - 165, 1978pdf D.Doo, M.Sabin: ''Behaviour of recursive division surfaces near extraordinary points'', Computer Aided Design, pp. 356-360, 1978 The Doo-Sabin process generates one new face at each original vertex, new faces along each original edge, and new faces at each original face. A primary characteristic of the Doo–Sabin subdivision method is the creation of four faces and four edges ('' Degree (graph theory), valence'' 4) around every new vertex in the refined mesh. A drawback is that the f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catmull–Clark Subdivision Surface
The Catmull–Clark algorithm is a technique used in 3D computer graphics to create curved surfaces by using subdivision surface modeling. It was devised by Edwin Catmull and Jim Clark in 1978 as a generalization of bi-cubic ''uniform'' B-spline surfaces to arbitrary topology. In 2005/06, Edwin Catmull, together with Tony DeRose and Jos Stam, received an Academy Award for Technical Achievement for their invention and application of subdivision surfaces. DeRose wrote about "efficient, fair interpolation" and character animation. Stam described a technique for a direct evaluation of the limit surface without recursion. Recursive evaluation Catmull–Clark surfaces are defined recursively, using the following ''refinement scheme.'' Start with a mesh of an arbitrary polyhedron. All the vertices in this mesh shall be called ''original points''. * For each face, add a ''face point'' ** Set each face point to be the average of all ''original points'' for the respective face * F ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
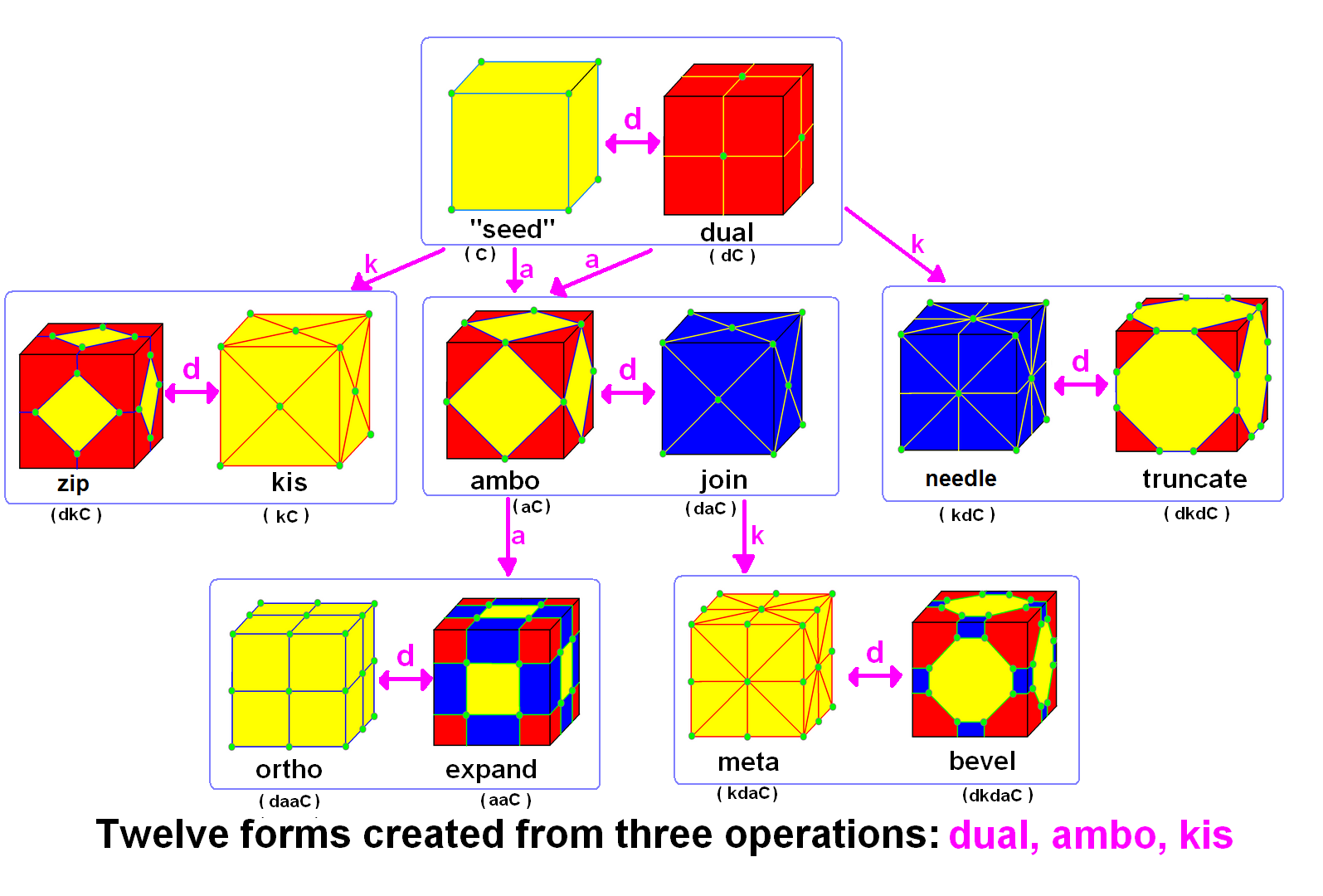
Conway Polyhedron Notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations. Conway and Hart extended the idea of using operators, like truncation as defined by Kepler, to build related polyhedra of the same symmetry. For example, represents a truncated cube, and , parsed as , is ( topologically) a truncated cuboctahedron. The simplest operator dual swaps vertex and face elements; e.g., a dual cube is an octahedron: . Applied in a series, these operators allow many higher order polyhedra to be generated. Conway defined the operators (ambo), (bevel), ( dual), (expand), (gyro), (join), (kis), (meta), (ortho), ( snub), and ( truncate), while Hart added ( reflect) and (propellor). Later implementations named further operators, sometimes referred to as "extended" operators. Conway's basic operations are sufficient to generate the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expansion (geometry)
In geometry, expansion is a polytope operation where Facet (mathematics), facets are separated and moved radially apart, and new facets are formed at separated elements (Vertex (geometry), vertices, Edge (geometry), edges, etc.). Equivalently this operation can be imagined by keeping facets in the same position but reducing their size. The expansion of a Regular polytope, regular convex polytope creates a uniform polytope, uniform convex polytope. For polyhedra, an expanded polyhedron has all the Face (geometry), faces of the original polyhedron, all the faces of the dual polyhedron, and new square faces in place of the original edges. Expansion of regular polytopes According to Coxeter, this multidimensional term was defined by Alicia Boole StottCoxeter, ''Regular Polytopes'' (1973), p. 123. p.210 for creating new polytopes, specifically starting from regular polytopes to construct new uniform polytopes. The ''expansion'' operation is symmetric with respect to a regular p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagonalizable Matrix
In linear algebra, a square matrix A is called diagonalizable or non-defective if it is matrix similarity, similar to a diagonal matrix. That is, if there exists an invertible matrix P and a diagonal matrix D such that . This is equivalent to (Such D are not unique.) This property exists for any linear map: for a dimension (vector space), finite-dimensional vector space a linear map T:V\to V is called diagonalizable if there exists an Basis (linear algebra)#Ordered bases and coordinates, ordered basis of V consisting of eigenvectors of T. These definitions are equivalent: if T has a matrix (mathematics), matrix representation A = PDP^ as above, then the column vectors of P form a basis consisting of eigenvectors of and the diagonal entries of D are the corresponding eigenvalues of with respect to this eigenvector basis, T is represented by Diagonalization is the process of finding the above P and and makes many subsequent computations easier. One can raise a diag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jos Stam
Jos Stam (born 28 December 1965 in The Hague, Netherlands) is a researcher in the field of computer graphics, focusing on the simulation of natural physical phenomena for 3D- computer animation. He achieved technical breakthroughs with the simulation of fluids and gases, new rendering algorithms and subdivision surfaces, which are a mix between two previously incompatible worlds of Nurbs- and polygon-modeling in 3D. Education and career Jos Stam's maternal grandfather was the Dutch politician Sim Visser. His father Jos Stam was born in Rotterdam (Netherlands), and in 1944 at the , he was deported by the Nazis to Germany, where he had to repair railroads behind the western front, until being liberated by the American troops in 1945. He emigrated to the US in 1956, where he worked as a researcher for the DuPont de Nemours Company. He became a US citizen in 1964. In the US he met his wife, Alida Wilhelmina Visser, born in Wassenaar (Netherlands). In early 1965, Jos' father was ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coplanar
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. However, a set of four or more distinct points will, in general, not lie in a single plane. Two lines in three-dimensional space are coplanar if there is a plane that includes them both. This occurs if the lines are parallel, or if they intersect each other. Two lines that are not coplanar are called skew lines. Distance geometry provides a solution technique for the problem of determining whether a set of points is coplanar, knowing only the distances between them. Properties in three dimensions In three-dimensional space, two linearly independent vectors with the same initial point determine a plane through that point. Their cross product is a normal vector to that plane, and any vector orthogonal to this cross product through the in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3D Computer Graphics
3D computer graphics, sometimes called Computer-generated imagery, CGI, 3D-CGI or three-dimensional Computer-generated imagery, computer graphics, are graphics that use a three-dimensional representation of geometric data (often Cartesian coordinate system#Cartesian coordinates in three dimensions, Cartesian) that is stored in the computer for the purposes of performing calculations and rendering digital images, usually 2D images but sometimes 3D images. The resulting images may be stored for viewing later (possibly as an Computer animation, animation) or displayed in Real-time computer graphics, real time. 3D computer graphics, contrary to what the name suggests, are most often displayed on two-dimensional displays. Unlike 3D film and similar techniques, the result is two-dimensional, without visual depth perception, depth. More often, 3D graphics are being displayed on 3D displays, like in virtual reality systems. 3D graphics stand in contrast to 2D computer graphics which t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
N-gons
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain. The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon's '' vertices'' or ''corners''. An ''n''-gon is a polygon with ''n'' sides; for example, a triangle is a 3-gon. A simple polygon is one which does not intersect itself. More precisely, the only allowed intersections among the line segments that make up the polygon are the shared endpoints of consecutive segments in the polygonal chain. A simple polygon is the boundary of a region of the plane that is called a ''solid polygon''. The interior of a solid polygon is its ''body'', also known as a ''polygonal region'' or ''polygonal area''. In contexts where one is concerned only with simple and solid polygons, a ''polygon'' may refer only to a simple polygon or to a solid polygon. A polygonal chain may cross over itself, creating star polygon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (graph Theory)
In graph theory, the degree (or valency) of a vertex of a graph is the number of edges that are incident to the vertex; in a multigraph, a loop contributes 2 to a vertex's degree, for the two ends of the edge. The degree of a vertex v is denoted \deg(v) or \deg v. The maximum degree of a graph G is denoted by \Delta(G), and is the maximum of G's vertices' degrees. The minimum degree of a graph is denoted by \delta(G), and is the minimum of G's vertices' degrees. In the multigraph shown on the right, the maximum degree is 5 and the minimum degree is 0. In a regular graph, every vertex has the same degree, and so we can speak of ''the'' degree of the graph. A complete graph (denoted K_n, where n is the number of vertices in the graph) is a special kind of regular graph where all vertices have the maximum possible degree, n-1. In a signed graph, the number of positive edges connected to the vertex v is called positive deg(v) and the number of connected negative edges is enti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |