Doo–Sabin Subdivision Surface on:
[Wikipedia]
[Google]
[Amazon]
 In
In
pdf
D.Doo, M.Sabin: ''Behaviour of recursive division surfaces near extraordinary points'', Computer Aided Design, pp. 356-360, 1978
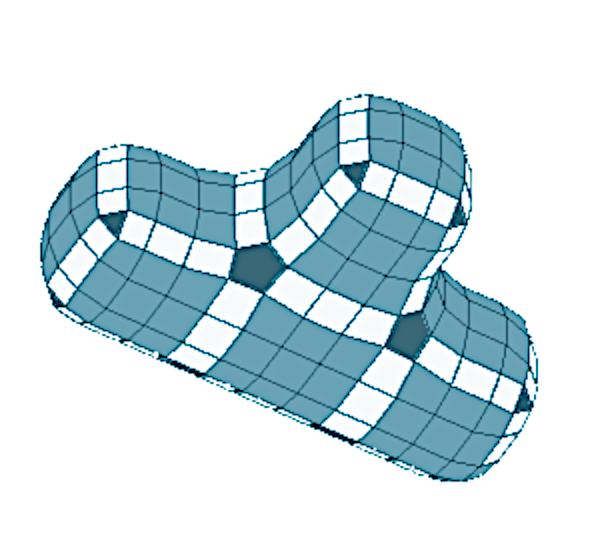
The Doo-Sabin process generates one new face at each original vertex, new faces along each original edge, and new faces at each original face. A primary characteristic of the Doo–Sabin subdivision method is the creation of four faces and four edges ('' Degree (graph theory), valence'' 4) around every new vertex in the refined mesh. A drawback is that the faces created at the original vertices may be triangles or n-gons that are not necessarily
pdf
The solution is, however, not as computationally efficient as for Catmull–Clark surfaces because the Doo–Sabin subdivision matrices are not (in general)
Doo–Sabin surfaces
3D computer graphics Multivariate interpolation {{Comp-sci-stub
 In
In 3D computer graphics
3D computer graphics, sometimes called Computer-generated imagery, CGI, 3D-CGI or three-dimensional Computer-generated imagery, computer graphics, are graphics that use a three-dimensional representation of geometric data (often Cartesian coor ...
, a Doo–Sabin subdivision surface is a type of subdivision surface
In the field of 3D computer graphics, a subdivision surface (commonly shortened to SubD surface or Subsurf) is a curved Computer representation of surfaces, surface represented by the specification of a coarser polygon mesh and produced by a re ...
based on a generalization of '' bi-quadratic'' uniform B-spline
In numerical analysis, a B-spline (short for basis spline) is a type of Spline (mathematics), spline function designed to have minimal Support (mathematics), support (overlap) for a given Degree of a polynomial, degree, smoothness, and set of bre ...
s, whereas Catmull-Clark was based on generalized '' bi-cubic'' uniform B-splines. The subdivision refinement algorithm was developed in 1978 by Daniel Doo and Malcolm Sabin.D. Doo: ''A subdivision algorithm for smoothing down irregularly shaped polyhedrons'', Proceedings on Interactive Techniques in Computer Aided Design, pp. 157 - 165, 1978D.Doo, M.Sabin: ''Behaviour of recursive division surfaces near extraordinary points'', Computer Aided Design, pp. 356-360, 1978
The Doo-Sabin process generates one new face at each original vertex, new faces along each original edge, and new faces at each original face. A primary characteristic of the Doo–Sabin subdivision method is the creation of four faces and four edges ('' Degree (graph theory), valence'' 4) around every new vertex in the refined mesh. A drawback is that the faces created at the original vertices may be triangles or n-gons that are not necessarily
coplanar
In geometry, a set of points in space are coplanar if there exists a geometric plane that contains them all. For example, three points are always coplanar, and if the points are distinct and non-collinear, the plane they determine is unique. How ...
.
Evaluation
Doo–Sabin surfaces are defined recursively. Like all subdivision procedures, each refinement iteration, following the procedure given, replaces the current mesh with a "smoother", more refined mesh. After many iterations, the surface will gradually converge onto a smooth limit surface. Just as for Catmull–Clark surfaces, Doo–Sabin limit surfaces can also be ''evaluated directly'' without any recursive refinement, by means of the technique of Jos Stam.Jos Stam, ''Exact Evaluation of Catmull–Clark Subdivision Surfaces at Arbitrary Parameter Values'', Proceedings of SIGGRAPH'98. In Computer Graphics Proceedings, ACM SIGGRAPH, 1998, 395–404The solution is, however, not as computationally efficient as for Catmull–Clark surfaces because the Doo–Sabin subdivision matrices are not (in general)
diagonalizable
In linear algebra, a square matrix A is called diagonalizable or non-defective if it is similar to a diagonal matrix. That is, if there exists an invertible matrix P and a diagonal matrix D such that . This is equivalent to (Such D are not ...
.
See also
* Expansion (equivalent geometric operation) - facets are moved apart after being separated, and new facets are formed *Conway polyhedron notation
In geometry and topology, Conway polyhedron notation, invented by John Horton Conway and promoted by George W. Hart, is used to describe polyhedra based on a seed polyhedron modified by various prefix operations.
Conway and Hart extended the i ...
- a set of related topological polyhedron and polygonal mesh operators
* Catmull-Clark subdivision surface
* Loop subdivision surface
External links
Doo–Sabin surfaces
3D computer graphics Multivariate interpolation {{Comp-sci-stub