|
Discrete Phase-type Distribution
The discrete phase-type distribution is a probability distribution that results from a system of one or more inter-related geometric distributions occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process. The distribution can be represented by a random variable describing the time until absorption of an absorbing Markov chain with one absorbing state. Each of the states of the Markov chain represents one of the phases. It has continuous time equivalent in the phase-type distribution. Definition A terminating Markov chain is a Markov chain where all states are transient, except one which is absorbing. Reordering the states, the transition probability matrix of a terminating Markov chain with m transient states is : =\left begin&\mathbf^0\\\mathbf^\mathsf&1\end\right where is a m\times m matrix, \mathbf^0 and \mathbf are column vectors with m entries, and \mathbf^0+\mathbf=\mathbf. The transition matrix is charact ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Degenerate Distribution
In probability theory, a degenerate distribution on a measure space (E, \mathcal, \mu) is a probability distribution whose support is a null set with respect to \mu. For instance, in the -dimensional space endowed with the Lebesgue measure, any distribution concentrated on a -dimensional subspace with is a degenerate distribution on . This is essentially the same notion as a singular probability measure, but the term ''degenerate'' is typically used when the distribution arises as a limit of (non-degenerate) distributions. When the support of a degenerate distribution consists of a single point , this distribution is a Dirac measure in : it is the distribution of a deterministic random variable equal to with probability 1. This is a special case of a discrete distribution; its probability mass function equals 1 in and 0 everywhere else. In the case of a real-valued random variable, the cumulative distribution function of the degenerate distribution localized in is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Discrete Distributions
Discrete may refer to: *Discrete particle or quantum in physics, for example in quantum theory *Discrete device, an electronic component with just one circuit element, either passive or active, other than an integrated circuit *Discrete group, a group with the discrete topology *Discrete category, category whose only arrows are identity arrows *Discrete mathematics, the study of structures without continuity *Discrete optimization, a branch of optimization in applied mathematics and computer science *Discrete probability distribution, a random variable that can be counted *Discrete space, a simple example of a topological space *Discrete spline interpolation, the discrete analog of ordinary spline interpolation *Discrete time, non-continuous time, which results in discrete-time samples *Discrete variable In mathematics and statistics, a quantitative variable may be continuous or discrete. If it can take on two real values and all the values between them, the variable is con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
 |
Queueing Theory
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research because the results are often used when making business decisions about the resources needed to provide a service. Queueing theory has its origins in research by Agner Krarup Erlang, who created models to describe the system of incoming calls at the Copenhagen Telephone Exchange Company. These ideas were seminal to the field of teletraffic engineering and have since seen applications in telecommunications, traffic engineering, computing, project management, and particularly industrial engineering, where they are applied in the design of factories, shops, offices, and hospitals. Spelling The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is '' Queue ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Phase-type Distribution
A phase-type distribution is a probability distribution constructed by a convolution or mixture of exponential distributions. It results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occurs may itself be a stochastic process. The distribution can be represented by a random variable describing the time until absorption of a Markov process with one absorbing state. Each of the Markov process, states of the Markov process represents one of the phases. It has a discrete time, discrete-time equivalent the discrete phase-type distribution. The set of phase-type distributions is dense in the field of all positive-valued distributions, that is, it can be used to approximate any positive-valued distribution. Definition Consider a continuous-time Markov process with ''m'' + 1 states, where ''m'' ≥ 1, such that the states 1,...,''m'' are transient states and state 0 is an absorbi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
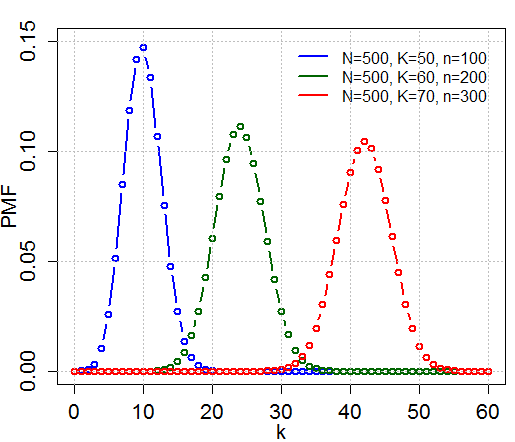 |
Hypergeometric Distribution
In probability theory and statistics, the hypergeometric distribution is a Probability distribution#Discrete probability distribution, discrete probability distribution that describes the probability of k successes (random draws for which the object drawn has a specified feature) in n draws, ''without'' replacement, from a finite Statistical population, population of size N that contains exactly K objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of k successes in n draws ''with'' replacement. Definitions Probability mass function The following conditions characterize the hypergeometric distribution: * The result of each draw (the elements of the population being sampled) can be classified into one of Binary variable, two mutually exclusive categories (e.g. Pass/Fail or Employed/Unemployed). * The probability of a success changes on each draw, as each draw decreases the population ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
Hyperexponential Distribution
In probability theory, a hyperexponential distribution is a continuous probability distribution whose probability density function of the random variable ''X'' is given by : f_X(x) = \sum_^n f_(x)\;p_i, where each ''Y''''i'' is an exponentially distributed random variable with rate parameter ''λ''''i'', and ''p''''i'' is the probability that ''X'' will take on the form of the exponential distribution with rate ''λ''''i''. It is named the ''hyper''exponential distribution since its coefficient of variation is greater than that of the exponential distribution, whose coefficient of variation is 1, and the hypoexponential distribution, which has a coefficient of variation smaller than one. While the exponential distribution is the continuous analogue of the geometric distribution, the hyperexponential distribution is not analogous to the hypergeometric distribution. The hyperexponential distribution is an example of a mixture density. An example of a hyperexponential random varia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Negative Binomial Distribution
In probability theory and statistics, the negative binomial distribution, also called a Pascal distribution, is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified/constant/fixed number of successes r occur. For example, we can define rolling a 6 on some dice as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success (r=3). In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution. An alternative formulation is to model the number of total trials (instead of the number of failures). In fact, for a specified (non-random) number of successes , the number of failures is random because the number of total trials is random. For example, we could use the negative binomial distribution to model the number of days (random) a certain machin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Geometric Distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions: * The probability distribution of the number X of Bernoulli trials needed to get one success, supported on \mathbb = \; * The probability distribution of the number Y=X-1 of failures before the first success, supported on \mathbb_0 = \ . These two different geometric distributions should not be confused with each other. Often, the name ''shifted'' geometric distribution is adopted for the former one (distribution of X); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the support explicitly. The geometric distribution gives the probability that the first occurrence of success requires k independent trials, each with success probability p. If the probability of success on each trial is p, then the probability that the k-th trial is the first success is :\Pr(X = k) = (1-p)^p for k=1,2,3,4,\dots The above form of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Identity Matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. It has unique properties, for example when the identity matrix represents a geometric transformation, the object remains unchanged by the transformation. In other contexts, it is analogous to multiplying by the number 1. Terminology and notation The identity matrix is often denoted by I_n, or simply by I if the size is immaterial or can be trivially determined by the context. I_1 = \begin 1 \end ,\ I_2 = \begin 1 & 0 \\ 0 & 1 \end ,\ I_3 = \begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end ,\ \dots ,\ I_n = \begin 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \end. The term unit matrix has also been widely used, but the term ''identity matrix'' is now standard. The term ''unit matrix'' is ambiguous, because it is also used for a matrix of on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
|
|
Geometric Distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions: * The probability distribution of the number X of Bernoulli trials needed to get one success, supported on \mathbb = \; * The probability distribution of the number Y=X-1 of failures before the first success, supported on \mathbb_0 = \ . These two different geometric distributions should not be confused with each other. Often, the name ''shifted'' geometric distribution is adopted for the former one (distribution of X); however, to avoid ambiguity, it is considered wise to indicate which is intended, by mentioning the support explicitly. The geometric distribution gives the probability that the first occurrence of success requires k independent trials, each with success probability p. If the probability of success on each trial is p, then the probability that the k-th trial is the first success is :\Pr(X = k) = (1-p)^p for k=1,2,3,4,\dots The above form of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |