Queueing Theory on:
[Wikipedia]
[Google]
[Amazon]
 Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of
 However, the queueing node is not quite a pure black box since some information is needed about the inside of the queueing node. The queue has one or more ''servers'' which can each be paired with an arriving job. When the job is completed and departs, that server will again be free to be paired with another arriving job.
However, the queueing node is not quite a pure black box since some information is needed about the inside of the queueing node. The queue has one or more ''servers'' which can each be paired with an arriving job. When the job is completed and departs, that server will again be free to be paired with another arriving job.
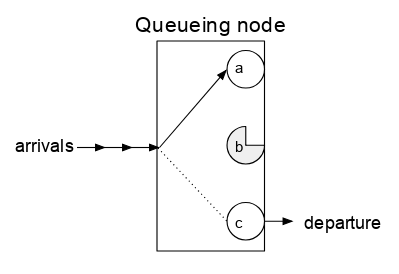 An analogy often used is that of the cashier at a supermarket. Customers arrive, are processed by the cashier, and depart. Each cashier processes one customer at a time, and hence this is a queueing node with only one server. A setting where a customer will leave immediately if the cashier is busy when the customer arrives, is referred to as a queue with no ''buffer'' (or no ''waiting area''). A setting with a waiting zone for up to ''n'' customers is called a queue with a buffer of size ''n''.
An analogy often used is that of the cashier at a supermarket. Customers arrive, are processed by the cashier, and depart. Each cashier processes one customer at a time, and hence this is a queueing node with only one server. A setting where a customer will leave immediately if the cashier is busy when the customer arrives, is referred to as a queue with no ''buffer'' (or no ''waiting area''). A setting with a waiting zone for up to ''n'' customers is called a queue with a buffer of size ''n''.
 Also called ''first-come, first-served'' (FCFS), this principle states that customers are served one at a time and that the customer that has been waiting the longest is served first.Penttinen A., ''Chapter 8 – Queueing Systems'', Lecture Notes: S-38.145 - Introduction to Teletraffic Theory.
; Last in, first out: This principle also serves customers one at a time, but the customer with the shortest waiting time will be served first. Also known as a stack.
; Processor sharing: Service capacity is shared equally between customers.
; Priority: Customers with high priority are served first. Priority queues can be of two types: ''non-preemptive'' (where a job in service cannot be interrupted) and ''preemptive'' (where a job in service can be interrupted by a higher-priority job). No work is lost in either model.
; Shortest job first: The next job to be served is the one with the smallest size.
; Preemptive shortest job first: The next job to be served is the one with the smallest original size.
; Shortest remaining processing time: The next job to serve is the one with the smallest remaining processing requirement.
; Service facility
* Single server: customers line up and there is only one server
* Several parallel servers (single queue): customers line up and there are several servers
* Several parallel servers (several queues): there are many counters and customers can decide for which to queue
; Unreliable server
Server failures occur according to a stochastic (random) process (usually Poisson) and are followed by setup periods during which the server is unavailable. The interrupted customer remains in the service area until server is fixed.
; Customer waiting behavior
* Balking: customers decide not to join the queue if it is too long
* Jockeying: customers switch between queues if they think they will get served faster by doing so
* Reneging: customers leave the queue if they have waited too long for service
Arriving customers not served (either due to the queue having no buffer, or due to balking or reneging by the customer) are also known as ''dropouts''. The average rate of dropouts is a significant parameter describing a queue.
Also called ''first-come, first-served'' (FCFS), this principle states that customers are served one at a time and that the customer that has been waiting the longest is served first.Penttinen A., ''Chapter 8 – Queueing Systems'', Lecture Notes: S-38.145 - Introduction to Teletraffic Theory.
; Last in, first out: This principle also serves customers one at a time, but the customer with the shortest waiting time will be served first. Also known as a stack.
; Processor sharing: Service capacity is shared equally between customers.
; Priority: Customers with high priority are served first. Priority queues can be of two types: ''non-preemptive'' (where a job in service cannot be interrupted) and ''preemptive'' (where a job in service can be interrupted by a higher-priority job). No work is lost in either model.
; Shortest job first: The next job to be served is the one with the smallest size.
; Preemptive shortest job first: The next job to be served is the one with the smallest original size.
; Shortest remaining processing time: The next job to serve is the one with the smallest remaining processing requirement.
; Service facility
* Single server: customers line up and there is only one server
* Several parallel servers (single queue): customers line up and there are several servers
* Several parallel servers (several queues): there are many counters and customers can decide for which to queue
; Unreliable server
Server failures occur according to a stochastic (random) process (usually Poisson) and are followed by setup periods during which the server is unavailable. The interrupted customer remains in the service area until server is fixed.
; Customer waiting behavior
* Balking: customers decide not to join the queue if it is too long
* Jockeying: customers switch between queues if they think they will get served faster by doing so
* Reneging: customers leave the queue if they have waited too long for service
Arriving customers not served (either due to the queue having no buffer, or due to balking or reneging by the customer) are also known as ''dropouts''. The average rate of dropouts is a significant parameter describing a queue.
Online
* * chap.15, pp. 380–412 * * * Leonard Kleinrock
(MIT, Cambridge, May 31, 1961) Proposal for a Ph.D. Thesis * Leonard Kleinrock. ''Information Flow in Large Communication Nets'' (RLE Quarterly Progress Report, July 1961) * Leonard Kleinrock. ''Communication Nets: Stochastic Message Flow and Delay'' (McGraw-Hill, New York, 1964) * * * *
Virtamo's Queueing Theory Course
LINE: a general-purpose engine to solve queueing models
{{Authority control Production planning Customer experience Operations research Formal sciences Rationing Network performance Markov models
 Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of
Queueing theory is the mathematical study of waiting lines, or queues. A queueing model is constructed so that queue lengths and waiting time can be predicted. Queueing theory is generally considered a branch of operations research
Operations research () (U.S. Air Force Specialty Code: Operations Analysis), often shortened to the initialism OR, is a branch of applied mathematics that deals with the development and application of analytical methods to improve management and ...
because the results are often used when making business decisions about the resources needed to provide a service.
Queueing theory has its origins in research by Agner Krarup Erlang, who created models to describe the system of incoming calls at the Copenhagen Telephone Exchange Company. These ideas were seminal to the field of teletraffic engineering and have since seen applications in telecommunications
Telecommunication, often used in its plural form or abbreviated as telecom, is the transmission of information over a distance using electronic means, typically through cables, radio waves, or other communication technologies. These means of ...
, traffic engineering, computing
Computing is any goal-oriented activity requiring, benefiting from, or creating computer, computing machinery. It includes the study and experimentation of algorithmic processes, and the development of both computer hardware, hardware and softw ...
, project management
Project management is the process of supervising the work of a Project team, team to achieve all project goals within the given constraints. This information is usually described in project initiation documentation, project documentation, crea ...
, and particularly industrial engineering
Industrial engineering (IE) is concerned with the design, improvement and installation of integrated systems of people, materials, information, equipment and energy. It draws upon specialized knowledge and skill in the mathematical, physical, an ...
, where they are applied in the design of factories, shops, offices, and hospitals.
Spelling
The spelling "queueing" over "queuing" is typically encountered in the academic research field. In fact, one of the flagship journals of the field is '' Queueing Systems''.Description
Queueing theory is one of the major areas of study in the discipline ofmanagement science
Management science (or managerial science) is a wide and interdisciplinary study of solving complex problems and making strategic decisions as it pertains to institutions, corporations, governments and other types of organizational entities. It is ...
. Through management science, businesses are able to solve a variety of problems using different scientific and mathematical approaches. Queueing analysis is the probabilistic analysis of waiting lines, and thus the results, also referred to as the operating characteristics, are probabilistic rather than deterministic. The probability that n customers are in the queueing system, the average number of customers in the queueing system, the average number of customers in the waiting line, the average time spent by a customer in the total queuing system, the average time spent by a customer in the waiting line, and finally the probability that the server is busy or idle are all of the different operating characteristics that these queueing models compute. The overall goal of queueing analysis is to compute these characteristics for the current system and then test several alternatives that could lead to improvement. Computing the operating characteristics for the current system and comparing the values to the characteristics of the alternative systems allows managers to see the pros and cons of each potential option. These systems help in the final decision making process by showing ways to increase savings, reduce waiting time, improve efficiency, etc. The main queueing models that can be used are the single-server waiting line system and the multiple-server waiting line system, which are discussed further below. These models can be further differentiated depending on whether service times are constant or undefined, the queue length is finite, the calling population is finite, etc.
Single queueing nodes
A ''queue'' or ''queueing node'' can be thought of as nearly a black box. ''Jobs'' (also called ''customers'' or ''requests'', depending on the field) arrive to the queue, possibly wait some time, take some time being processed, and then depart from the queue. However, the queueing node is not quite a pure black box since some information is needed about the inside of the queueing node. The queue has one or more ''servers'' which can each be paired with an arriving job. When the job is completed and departs, that server will again be free to be paired with another arriving job.
However, the queueing node is not quite a pure black box since some information is needed about the inside of the queueing node. The queue has one or more ''servers'' which can each be paired with an arriving job. When the job is completed and departs, that server will again be free to be paired with another arriving job.
 An analogy often used is that of the cashier at a supermarket. Customers arrive, are processed by the cashier, and depart. Each cashier processes one customer at a time, and hence this is a queueing node with only one server. A setting where a customer will leave immediately if the cashier is busy when the customer arrives, is referred to as a queue with no ''buffer'' (or no ''waiting area''). A setting with a waiting zone for up to ''n'' customers is called a queue with a buffer of size ''n''.
An analogy often used is that of the cashier at a supermarket. Customers arrive, are processed by the cashier, and depart. Each cashier processes one customer at a time, and hence this is a queueing node with only one server. A setting where a customer will leave immediately if the cashier is busy when the customer arrives, is referred to as a queue with no ''buffer'' (or no ''waiting area''). A setting with a waiting zone for up to ''n'' customers is called a queue with a buffer of size ''n''.
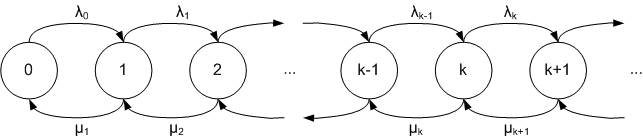
Birth-death process
The behaviour of a single queue (also called a ''queueing node'') can be described by a birth–death process, which describes the arrivals and departures from the queue, along with the number of jobs currently in the system. If ''k'' denotes the number of jobs in the system (either being serviced or waiting if the queue has a buffer of waiting jobs), then an arrival increases ''k'' by 1 and a departure decreases ''k'' by 1. The system transitions between values of ''k'' by "births" and "deaths", which occur at the arrival rates and the departure rates for each job . For a queue, these rates are generally considered not to vary with the number of jobs in the queue, so a singleaverage
In colloquial, ordinary language, an average is a single number or value that best represents a set of data. The type of average taken as most typically representative of a list of numbers is the arithmetic mean the sum of the numbers divided by ...
rate of arrivals/departures per unit time is assumed. Under this assumption, this process has an arrival rate of and a departure rate of .

Balance equations
The steady state equations for the birth-and-death process, known as the balance equations, are as follows. Here denotes the steady state probability to be in state ''n''. : : : The first two equations imply : and : . By mathematical induction, : . The condition leads to : which, together with the equation for , fully describes the required steady state probabilities.Kendall's notation
Single queueing nodes are usually described using Kendall's notation in the form A/S/''c'' where ''A'' describes the distribution of durations between each arrival to the queue, ''S'' the distribution of service times for jobs, and ''c'' the number of servers at the node.Tijms, H.C, ''Algorithmic Analysis of Queues'', Chapter 9 in A First Course in Stochastic Models, Wiley, Chichester, 2003 For an example of the notation, the M/M/1 queue is a simple model where a single server serves jobs that arrive according to a Poisson process (where inter-arrival durations are exponentially distributed) and have exponentially distributed service times (the M denotes aMarkov process
In probability theory and statistics, a Markov chain or Markov process is a stochastic process describing a sequence of possible events in which the probability of each event depends only on the state attained in the previous event. Informally, ...
). In an M/G/1 queue, the G stands for "general" and indicates an arbitrary probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
for service times.
Example analysis of an M/M/1 queue
Consider a queue with one server and the following characteristics: * '''': the arrival rate (the reciprocal of the expected time between each customer arriving, e.g. 10 customers per second) * '''': the reciprocal of the mean service time (the expected number of consecutive service completions per the same unit time, e.g. per 30 seconds) * ''n'': the parameter characterizing the number of customers in the system * : the probability of there being ''n'' customers in the system in steady state Further, let represent the number of times the system enters state ''n'', and represent the number of times the system leaves state ''n''. Then for all ''n''. That is, the number of times the system leaves a state differs by at most 1 from the number of times it enters that state, since it will either return into that state at some time in the future () or not (). When the system arrives at a steady state, the arrival rate should be equal to the departure rate. Thus the balance equations : : : imply : The fact that leads to thegeometric distribution
In probability theory and statistics, the geometric distribution is either one of two discrete probability distributions:
* The probability distribution of the number X of Bernoulli trials needed to get one success, supported on \mathbb = \;
* T ...
formula
:
where .
Simple two-equation queue
A common basic queueing system is attributed to Erlang and is a modification of Little's Law. Given an arrival rate ''λ'', a dropout rate ''σ'', and a departure rate ''μ'', length of the queue ''L'' is defined as: : . Assuming an exponential distribution for the rates, the waiting time ''W'' can be defined as the proportion of arrivals that are served. This is equal to the exponential survival rate of those who do not drop out over the waiting period, giving: : The second equation is commonly rewritten as: : The two-stage one-box model is common inepidemiology
Epidemiology is the study and analysis of the distribution (who, when, and where), patterns and Risk factor (epidemiology), determinants of health and disease conditions in a defined population, and application of this knowledge to prevent dise ...
.
History
In 1909, Agner Krarup Erlang, a Danish engineer who worked for the Copenhagen Telephone Exchange, published the first paper on what would now be called queueing theory. He modeled the number of telephone calls arriving at an exchange by a Poisson process and solved the M/D/1 queue in 1917 and M/D/''k'' queueing model in 1920. In Kendall's notation: * M stands for "Markov" or "memoryless", and means arrivals occur according to a Poisson process * D stands for "deterministic", and means jobs arriving at the queue require a fixed amount of service * ''k'' describes the number of servers at the queueing node (''k'' = 1, 2, 3, ...) If the node has more jobs than servers, then jobs will queue and wait for service. The M/G/1 queue was solved by Felix Pollaczek in 1930, a solution later recast in probabilistic terms by Aleksandr Khinchin and now known as the Pollaczek–Khinchine formula. After the 1940s, queueing theory became an area of research interest to mathematicians. In 1953, David George Kendall solved the GI/M/''k'' queue and introduced the modern notation for queues, now known as Kendall's notation. In 1957, Pollaczek studied the GI/G/1 using an integral equation. John Kingman gave a formula for the mean waiting time in a G/G/1 queue, now known as Kingman's formula. Leonard Kleinrock worked on the application of queueing theory to message switching in the early 1960s andpacket switching
In telecommunications, packet switching is a method of grouping Data (computing), data into short messages in fixed format, i.e. ''network packet, packets,'' that are transmitted over a digital Telecommunications network, network. Packets consi ...
in the early 1970s. His initial contribution to this field was his doctoral thesis at the Massachusetts Institute of Technology
The Massachusetts Institute of Technology (MIT) is a Private university, private research university in Cambridge, Massachusetts, United States. Established in 1861, MIT has played a significant role in the development of many areas of moder ...
in 1962, published in book form in 1964. His theoretical work published in the early 1970s underpinned the use of packet switching in the ARPANET
The Advanced Research Projects Agency Network (ARPANET) was the first wide-area packet-switched network with distributed control and one of the first computer networks to implement the TCP/IP protocol suite. Both technologies became the tec ...
, a forerunner to the Internet.
The matrix geometric method and matrix analytic methods have allowed queues with phase-type distributed inter-arrival and service time distributions to be considered.
Systems with coupled orbits are an important part in queueing theory in the application to wireless networks and signal processing.
Modern day application of queueing theory concerns among other things product development
New product development (NPD) or product development in business and engineering covers the complete process of launching a new product to the market. Product development also includes the renewal of an existing product and introducing a product ...
where (material) products have a spatiotemporal existence, in the sense that products have a certain volume and a certain duration.
Problems such as performance metrics for the M/G/''k'' queue remain an open problem.
Service disciplines
Various scheduling policies can be used at queueing nodes: ; First in, first out: Also called ''first-come, first-served'' (FCFS), this principle states that customers are served one at a time and that the customer that has been waiting the longest is served first.Penttinen A., ''Chapter 8 – Queueing Systems'', Lecture Notes: S-38.145 - Introduction to Teletraffic Theory.
; Last in, first out: This principle also serves customers one at a time, but the customer with the shortest waiting time will be served first. Also known as a stack.
; Processor sharing: Service capacity is shared equally between customers.
; Priority: Customers with high priority are served first. Priority queues can be of two types: ''non-preemptive'' (where a job in service cannot be interrupted) and ''preemptive'' (where a job in service can be interrupted by a higher-priority job). No work is lost in either model.
; Shortest job first: The next job to be served is the one with the smallest size.
; Preemptive shortest job first: The next job to be served is the one with the smallest original size.
; Shortest remaining processing time: The next job to serve is the one with the smallest remaining processing requirement.
; Service facility
* Single server: customers line up and there is only one server
* Several parallel servers (single queue): customers line up and there are several servers
* Several parallel servers (several queues): there are many counters and customers can decide for which to queue
; Unreliable server
Server failures occur according to a stochastic (random) process (usually Poisson) and are followed by setup periods during which the server is unavailable. The interrupted customer remains in the service area until server is fixed.
; Customer waiting behavior
* Balking: customers decide not to join the queue if it is too long
* Jockeying: customers switch between queues if they think they will get served faster by doing so
* Reneging: customers leave the queue if they have waited too long for service
Arriving customers not served (either due to the queue having no buffer, or due to balking or reneging by the customer) are also known as ''dropouts''. The average rate of dropouts is a significant parameter describing a queue.
Also called ''first-come, first-served'' (FCFS), this principle states that customers are served one at a time and that the customer that has been waiting the longest is served first.Penttinen A., ''Chapter 8 – Queueing Systems'', Lecture Notes: S-38.145 - Introduction to Teletraffic Theory.
; Last in, first out: This principle also serves customers one at a time, but the customer with the shortest waiting time will be served first. Also known as a stack.
; Processor sharing: Service capacity is shared equally between customers.
; Priority: Customers with high priority are served first. Priority queues can be of two types: ''non-preemptive'' (where a job in service cannot be interrupted) and ''preemptive'' (where a job in service can be interrupted by a higher-priority job). No work is lost in either model.
; Shortest job first: The next job to be served is the one with the smallest size.
; Preemptive shortest job first: The next job to be served is the one with the smallest original size.
; Shortest remaining processing time: The next job to serve is the one with the smallest remaining processing requirement.
; Service facility
* Single server: customers line up and there is only one server
* Several parallel servers (single queue): customers line up and there are several servers
* Several parallel servers (several queues): there are many counters and customers can decide for which to queue
; Unreliable server
Server failures occur according to a stochastic (random) process (usually Poisson) and are followed by setup periods during which the server is unavailable. The interrupted customer remains in the service area until server is fixed.
; Customer waiting behavior
* Balking: customers decide not to join the queue if it is too long
* Jockeying: customers switch between queues if they think they will get served faster by doing so
* Reneging: customers leave the queue if they have waited too long for service
Arriving customers not served (either due to the queue having no buffer, or due to balking or reneging by the customer) are also known as ''dropouts''. The average rate of dropouts is a significant parameter describing a queue.
Queueing networks
Queue networks are systems in which multiple queues are connected by ''customer routing''. When a customer is serviced at one node, it can join another node and queue for service, or leave the network. For networks of ''m'' nodes, the state of the system can be described by an ''m''–dimensional vector (''x''1, ''x''2, ..., ''x''''m'') where ''x''''i'' represents the number of customers at each node. The simplest non-trivial networks of queues are called tandem queues. The first significant results in this area were Jackson networks, for which an efficient product-form stationary distribution exists and the mean value analysis (which allows average metrics such as throughput and sojourn times) can be computed. If the total number of customers in the network remains constant, the network is called a ''closed network'' and has been shown to also have a product–form stationary distribution by the Gordon–Newell theorem. This result was extended to the BCMP network, where a network with very general service time, regimes, and customer routing is shown to also exhibit a product–form stationary distribution. The normalizing constant can be calculated with the Buzen's algorithm, proposed in 1973. Networks of customers have also been investigated, such as Kelly networks, where customers of different classes experience different priority levels at different service nodes. Another type of network are G-networks, first proposed by Erol Gelenbe in 1993: these networks do not assume exponential time distributions like the classic Jackson network.Routing algorithms
In discrete-time networks where there is a constraint on which service nodes can be active at any time, the max-weight scheduling algorithm chooses a service policy to give optimal throughput in the case that each job visits only a single-person service node. In the more general case where jobs can visit more than one node, backpressure routing gives optimal throughput. A network scheduler must choose a queueing algorithm, which affects the characteristics of the larger network.Mean-field limits
Mean-field models consider the limiting behaviour of the empirical measure (proportion of queues in different states) as the number of queues ''m'' approaches infinity. The impact of other queues on any given queue in the network is approximated by a differential equation. The deterministic model converges to the same stationary distribution as the original model.Heavy traffic/diffusion approximations
In a system with high occupancy rates (utilisation near 1), a heavy traffic approximation can be used to approximate the queueing length process by a reflected Brownian motion, Ornstein–Uhlenbeck process, or more general diffusion process. The number of dimensions of the Brownian process is equal to the number of queueing nodes, with the diffusion restricted to the non-negative orthant.Fluid limits
Fluid models are continuous deterministic analogs of queueing networks obtained by taking the limit when the process is scaled in time and space, allowing heterogeneous objects. This scaled trajectory converges to a deterministic equation which allows the stability of the system to be proven. It is known that a queueing network can be stable but have an unstable fluid limit.Queueing Applications
Queueing theory finds widespread application in computer science and information technology. In networking, for instance, queues are integral to routers and switches, where packets queue up for transmission. By applying queueing theory principles, designers can optimize these systems, ensuring responsive performance and efficient resource utilization. Beyond the technological realm, queueing theory is relevant to everyday experiences. Whether waiting in line at a supermarket or for public transportation, understanding the principles of queueing theory provides valuable insights into optimizing these systems for enhanced user satisfaction. At some point, everyone will be involved in an aspect of queuing. What some may view to be an inconvenience could possibly be the most effective method. Queueing theory, a discipline rooted in applied mathematics and computer science, is a field dedicated to the study and analysis of queues, or waiting lines, and their implications across a diverse range of applications. This theoretical framework has proven instrumental in understanding and optimizing the efficiency of systems characterized by the presence of queues. The study of queues is essential in contexts such as traffic systems, computer networks, telecommunications, and service operations. Queueing theory delves into various foundational concepts, with the arrival process and service process being central. The arrival process describes the manner in which entities join the queue over time, often modeled using stochastic processes like Poisson processes. The efficiency of queueing systems is gauged through key performance metrics. These include the average queue length, average wait time, and system throughput. These metrics provide insights into the system's functionality, guiding decisions aimed at enhancing performance and reducing wait times.Cooper, B. F., & Mitrani, I. (1985). ''Queueing Networks: A Fundamental Approach''. John Wiley & Sons.See also
* Ehrenfest model * Erlang unit *Line management
Line management refers to the management of employees who are directly involved in the production or delivery of products, goods and/or services. As the interface between an organisation and its front-line workforce, line management represents ...
* Network simulation
* Project production management
* Queue area
Queue areas are places in which people queue (first-come, first-served) for goods or services. Such a group of people is known as a ''queue'' (British English, British usage) or ''line'' (American English, American usage), and the people are ...
* Queueing delay
* Queue management system
* Queuing Rule of Thumb
* Random early detection
* Renewal theory
* Throughput
Network throughput (or just throughput, when in context) refers to the rate of message delivery over a communication channel in a communication network, such as Ethernet or packet radio. The data that these messages contain may be delivered ov ...
* Scheduling (computing)
In computing, scheduling is the action of assigning resources to perform tasks. The resources may be processors, network links or expansion cards. The tasks may be threads, processes or data flows.
The scheduling activity is carried out b ...
* Traffic jam
* Traffic generation model
* Flow network
References
Further reading
*Online
* * chap.15, pp. 380–412 * * * Leonard Kleinrock
(MIT, Cambridge, May 31, 1961) Proposal for a Ph.D. Thesis * Leonard Kleinrock. ''Information Flow in Large Communication Nets'' (RLE Quarterly Progress Report, July 1961) * Leonard Kleinrock. ''Communication Nets: Stochastic Message Flow and Delay'' (McGraw-Hill, New York, 1964) * * * *
External links
Virtamo's Queueing Theory Course
LINE: a general-purpose engine to solve queueing models
{{Authority control Production planning Customer experience Operations research Formal sciences Rationing Network performance Markov models