|
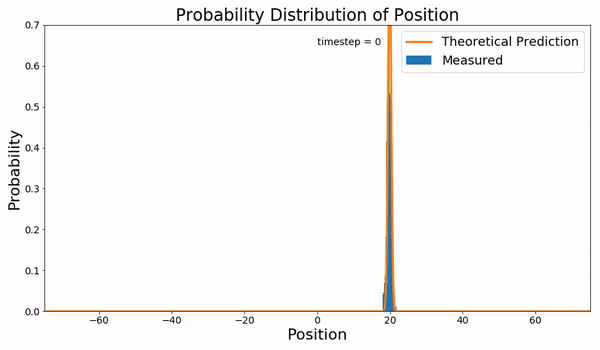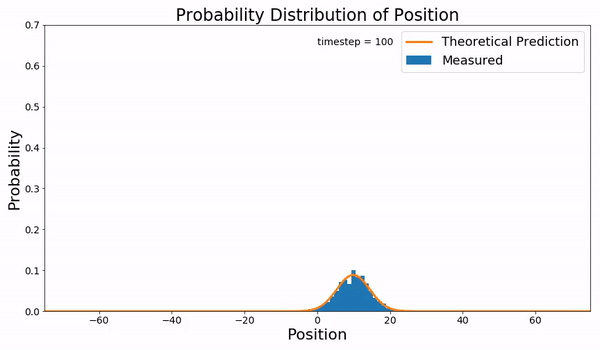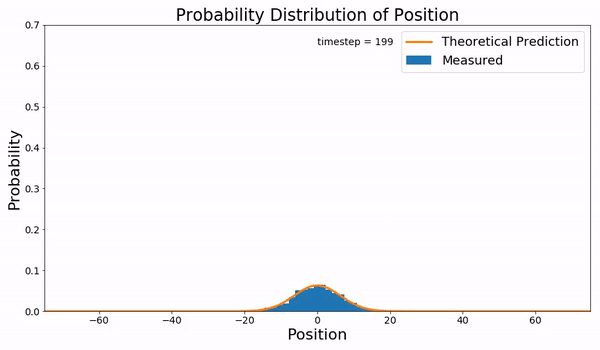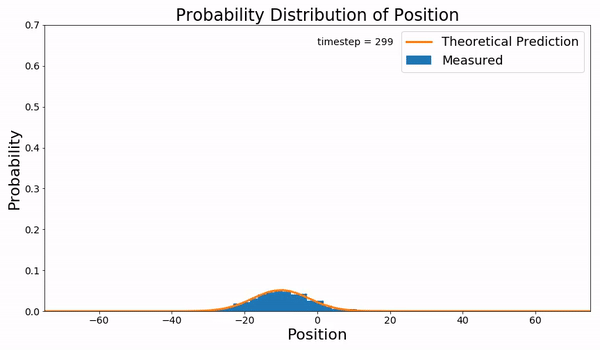
Diffusion Process
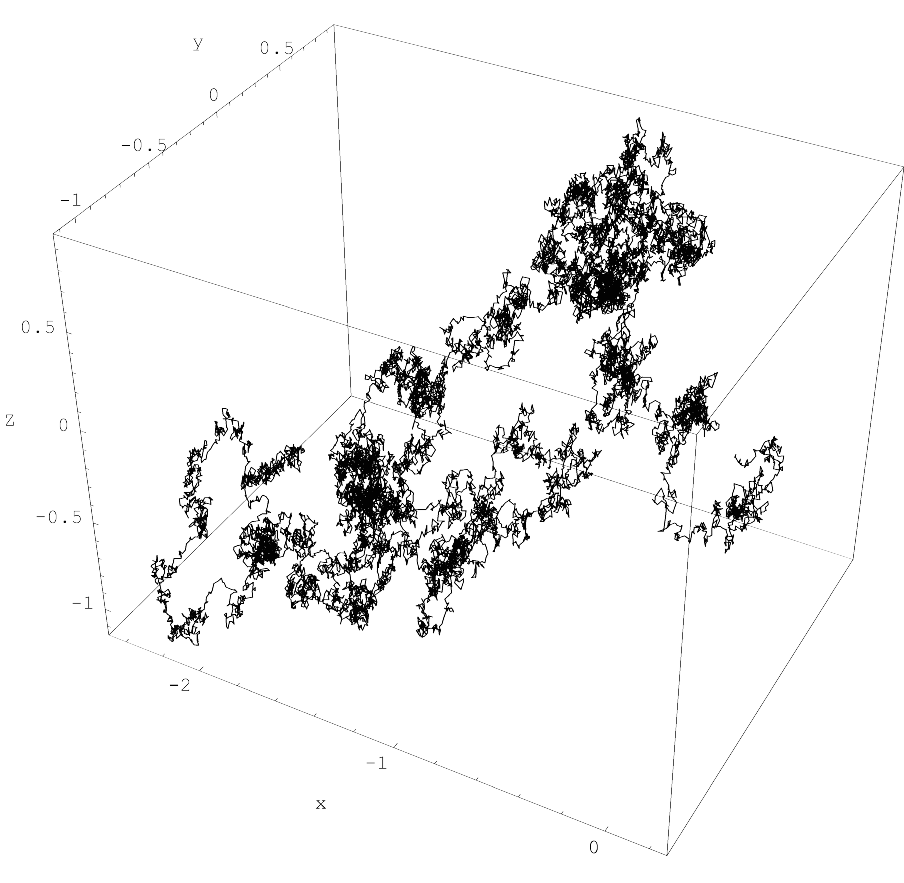
In probability theory and statistics, diffusion processes are a class of continuous-time Markov process with almost surely continuous sample paths. Diffusion process is stochastic in nature and hence is used to model many real-life stochastic systems. Brownian motion, reflected Brownian motion and Ornstein–Uhlenbeck processes are examples of diffusion processes. It is used heavily in statistical physics, statistical analysis, information theory, data science, neural networks, finance and marketing. A sample path of a diffusion process models the trajectory of a particle embedded in a flowing fluid and subjected to random displacements due to collisions with other particles, which is called Brownian motion. The position of the particle is then random; its probability density function as a function of space and time is governed by a convection–diffusion equation. Mathematical definition A ''diffusion process'' is a Markov process with continuous sample paths for which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probability Theory
Probability theory or probability calculus is the branch of mathematics concerned with probability. Although there are several different probability interpretations, probability theory treats the concept in a rigorous mathematical manner by expressing it through a set of axioms of probability, axioms. Typically these axioms formalise probability in terms of a probability space, which assigns a measure (mathematics), measure taking values between 0 and 1, termed the probability measure, to a set of outcomes called the sample space. Any specified subset of the sample space is called an event (probability theory), event. Central subjects in probability theory include discrete and continuous random variables, probability distributions, and stochastic processes (which provide mathematical abstractions of determinism, non-deterministic or uncertain processes or measured Quantity, quantities that may either be single occurrences or evolve over time in a random fashion). Although it is no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Marketing
Marketing is the act of acquiring, satisfying and retaining customers. It is one of the primary components of Business administration, business management and commerce. Marketing is usually conducted by the seller, typically a retailer or manufacturer. Products can be marketed to other businesses (B2B Marketing, B2B) or directly to consumers (B2C). Sometimes tasks are contracted to dedicated marketing firms, like a Media agency, media, market research, or advertising agency. Sometimes, a trade association or government agency (such as the Agricultural Marketing Service) advertises on behalf of an entire industry or locality, often a specific type of food (e.g. Got Milk?), food from a specific area, or a city or region as a tourism destination. Market orientations are philosophies concerning the factors that should go into market planning. The marketing mix, which outlines the specifics of the product and how it will be sold, including the channels that will be used to adverti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jump Diffusion
Jump diffusion is a stochastic process that involves jump process, jumps and diffusion process, diffusion. It has important applications in magnetic reconnection, coronal mass ejections, condensed matter physics, and pattern theory and computational vision. In physics In crystals, atomic diffusion typically consists of jumps between vacant lattice sites. On time and length scales that average over many single jumps, the net motion of the jumping atoms can be described as regular diffusion. Jump diffusion can be studied on a microscopic scale by inelastic neutron scattering and by Mößbauer spectroscopy. Closed expressions for the autocorrelation function have been derived for several jump(-diffusion) models: * Singwi, Sjölander 1960: alternation between oscillatory motion and directed motion * Chudley, Elliott 1961: jumps on a lattice * Sears 1966, 1967: jump diffusion of rotational degrees of freedom * Hall, Ross 1981: jump diffusion within a restricted volume In economics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Itô Diffusion
In mathematics – specifically, in stochastic analysis – an Itô diffusion is a solution to a specific type of stochastic differential equation. That equation is similar to the Langevin equation used in physics to describe the Brownian motion of a particle subjected to a potential in a viscous fluid. Itô diffusions are named after the Japanese mathematician Kiyosi Itô. Overview A (time-homogeneous) Itô diffusion in ''n''-dimensional Euclidean space \boldsymbol^n is a process ''X'' : , +∞) × Ω → R''n'' defined on a probability space (Ω, Σ, P) and satisfying a stochastic differential equation of the form :\mathrm X_ = b(X_t) \, \mathrm t + \sigma (X_) \, \mathrm B_, where ''B'' is an ''m''-dimensional Brownian motion and ''b'' : R''n'' → R''n'' and σ : R''n'' → R''n''×''m'' satisfy the usual Lipschitz continuity condition :, b(x) - b(y) , + , \sigma (x) - \sigma (y) , ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, as in spinodal decomposition. Diffusion is a stochastic process due to the inherent randomness of the diffusing entity and can be used to model many real-life stochastic scenarios. Therefore, diffusion and the corresponding mathematical models are used in several fields beyond physics, such as statistics, probability theory, information theory, neural networks, finance, and marketing. The concept of diffusion is widely used in many fields, including physics (Molecular diffusion, particle diffusion), chemistry, biology, sociology, economics, statistics, data science, and finance (diffusion of people, ideas, data and price v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Itô Calculus
Itô calculus, named after Kiyosi Itô, extends the methods of calculus to stochastic processes such as Brownian motion (see Wiener process). It has important applications in mathematical finance and stochastic differential equations. The central concept is the Itô stochastic integral, a stochastic generalization of the Riemann–Stieltjes integral in analysis. The integrands and the integrators are now stochastic processes: Y_t = \int_0^t H_s\,dX_s, where is a locally square-integrable process adapted to the filtration generated by , which is a Brownian motion or, more generally, a semimartingale. The result of the integration is then another stochastic process. Concretely, the integral from 0 to any particular is a random variable, defined as a limit of a certain sequence of random variables. The paths of Brownian motion fail to satisfy the requirements to be able to apply the standard techniques of calculus. So with the integrand a stochastic process, the Itô stochas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stochastic Differential Equation
A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs have many applications throughout pure mathematics and are used to model various behaviours of stochastic models such as stock prices,Musiela, M., and Rutkowski, M. (2004), Martingale Methods in Financial Modelling, 2nd Edition, Springer Verlag, Berlin. random growth models or physical systems that are subjected to thermal fluctuations. SDEs have a random differential that is in the most basic case random white noise calculated as the distributional derivative of a Brownian motion or more generally a semimartingale. However, other types of random behaviour are possible, such as jump processes like Lévy processes or semimartingales with jumps. Stochastic differential equations are in general neither differential equations nor random differential equations. Random differential equation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Fokker–Planck Equation
In statistical mechanics and information theory, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag (physics), drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. The Fokker–Planck equation has multiple applications in information theory, graph theory, data science, finance, economics etc. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. When applied to particle position and momentum distributions, it is known as the Klein–Kr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kolmogorov Equations
In probability theory, Kolmogorov equations characterize continuous-time Markov processes. In particular, they describe how the probability of a continuous-time Markov process in a certain state changes over time. There are four distinct equations: the Kolmogorov forward equation for continuous processes, now understood to be identical to the Fokker–Planck equation, the Kolmogorov forward equation for jump processes, and two Kolmogorov backward equations for processes with and without discontinuous jumps. Diffusion processes vs. jump processes Writing in 1931, Andrei Kolmogorov started from the theory of discrete time Markov processes, which are described by the Chapman–Kolmogorov equation, and sought to derive a theory of continuous time Markov processes by extending this equation. He found that there are two kinds of continuous time Markov processes, depending on the assumed behavior over small intervals of time: If you assume that "in a small time interval there is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sample-continuous Process
In mathematics, a sample-continuous process is a stochastic process whose sample paths are almost surely continuous functions. Definition Let (Ω, Σ, P) be a probability space. Let ''X'' : ''I'' × Ω → ''S'' be a stochastic process, where the index set ''I'' and state space ''S'' are both topological spaces. Then the process ''X'' is called sample-continuous (or almost surely continuous, or simply continuous) if the map ''X''(''ω'') : ''I'' → ''S'' is continuous as a function of topological spaces for P-almost all ''ω'' in ''Ω''. In many examples, the index set ''I'' is an interval of time, , ''T''or real_line.html" ;"title=", +∞), and the state space ''S'' is the real line">, +∞), and the state space ''S'' is the real line or ''n''-dimensional Euclidean space R''n''. Examples * Brownian motion (the Wiener process) on Euclidean space is sampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Convection–diffusion Equation
The convection–diffusion equation is a parabolic partial differential equation that combines the diffusion equation, diffusion and convection (advection equation, advection) equations. It describes physical phenomena where particles, energy, or other physical quantities are transferred inside a physical system due to two processes: diffusion and convection. Depending on context, the same equation can be called the advection–diffusion equation, drift velocity, drift–diffusion equation, or (generic) scalar transport equation. Equation The general equation in conservative form is \frac = \mathbf \cdot (D \mathbf c - \mathbf c) + R where * is the variable of interest (species concentration for mass transfer, temperature for heat transfer), * is the diffusivity (also called diffusion coefficient), such as mass diffusivity for particle motion or thermal diffusivity for heat transport, * is the velocity field that the quantity is moving with. It is a function of time and space. Fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Function Of Space And Time
Functions of space and time Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ... describe the evolution of a dynamic system or field, involving position (typically 'r') and time (t) (see Field equations) Spacetime Types of functions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |