|
Cultural Consensus Theory
Cultural consensus theory is an approach to information pooling (aggregation, data fusion) which supports a framework for the measurement and evaluation of beliefs as cultural; shared to some extent by a group of individuals. Cultural consensus models guide the aggregation of responses from individuals to estimate (1) the culturally appropriate answers to a series of related questions (when the answers are unknown) and (2) individual competence (cultural competence) in answering those questions. The theory is applicable when there is sufficient agreement across people to assume that a single set of answers exists. The agreement between pairs of individuals is used to estimate individual cultural competence. Answers are estimated by weighting responses of individuals by their competence and then combining responses. Theory Cultural consensus theory assumes that cultural beliefs are learned and shared across people and that there is a common understanding of what the world and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cultural
Culture ( ) is a concept that encompasses the social behavior, institutions, and Social norm, norms found in human societies, as well as the knowledge, beliefs, arts, laws, Social norm, customs, capabilities, Attitude (psychology), attitudes, and habits of the individuals in these groups.Tylor, Edward. (1871). ''Primitive Culture''. Vol 1. New York: J. P. Putnam's Son Culture often originates from or is attributed to a specific region or location. Humans acquire culture through the learning processes of enculturation and socialization, which is shown by the diversity of cultures across societies. A cultural norm codifies acceptable conduct in society; it serves as a guideline for behavior, dress, language, and demeanor in a situation, which serves as a template for expectations in a social group. Accepting only a monoculturalism, monoculture in a social group can bear risks, just as a single species can wither in the face of environmental change, for lack of functional respo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factor Analysis
Factor analysis is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. For example, it is possible that variations in six observed variables mainly reflect the variations in two unobserved (underlying) variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modelled as linear combinations of the potential factors plus "error" terms, hence factor analysis can be thought of as a special case of errors-in-variables models. Simply put, the factor loading of a variable quantifies the extent to which the variable is related to a given factor. A common rationale behind factor analytic methods is that the information gained about the interdependencies between observed variables can be used later to reduce the set of variables in a dataset. Factor analysis is commonly used in psychometrics, pers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cultural Anthropology
Cultural anthropology is a branch of anthropology focused on the study of cultural variation among humans. It is in contrast to social anthropology, which perceives cultural variation as a subset of a posited anthropological constant. The term sociocultural anthropology includes both cultural and social anthropology traditions. Anthropologists have pointed out that through culture, people can adapt to their environment in non-genetic ways, so people living in different environments will often have different cultures. Much of anthropological theory has originated in an appreciation of and interest in the tension between the local (particular cultures) and the global (a universal human nature, or the web of connections between people in distinct places/circumstances). Cultural anthropology has a rich methodology, including participant observation (often called fieldwork because it requires the anthropologist spending an extended period of time at the research location), inter ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlation Matrix
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Model
In statistics, the term linear model refers to any model which assumes linearity in the system. The most common occurrence is in connection with regression models and the term is often taken as synonymous with linear regression model. However, the term is also used in time series analysis with a different meaning. In each case, the designation "linear" is used to identify a subclass of models for which substantial reduction in the complexity of the related statistical theory is possible. Linear regression models For the regression case, the statistical model is as follows. Given a (random) sample (Y_i, X_, \ldots, X_), \, i = 1, \ldots, n the relation between the observations Y_i and the independent variables X_ is formulated as :Y_i = \beta_0 + \beta_1 \phi_1(X_) + \cdots + \beta_p \phi_p(X_) + \varepsilon_i \qquad i = 1, \ldots, n where \phi_1, \ldots, \phi_p may be nonlinear functions. In the above, the quantities \varepsilon_i are random variables representing err ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bayesian Probability
Bayesian probability ( or ) is an interpretation of the concept of probability, in which, instead of frequency or propensity of some phenomenon, probability is interpreted as reasonable expectation representing a state of knowledge or as quantification of a personal belief. The Bayesian interpretation of probability can be seen as an extension of propositional logic that enables reasoning with hypotheses; that is, with propositions whose truth or falsity is unknown. In the Bayesian view, a probability is assigned to a hypothesis, whereas under frequentist inference, a hypothesis is typically tested without being assigned a probability. Bayesian probability belongs to the category of evidential probabilities; to evaluate the probability of a hypothesis, the Bayesian probabilist specifies a prior probability. This, in turn, is then updated to a posterior probability in the light of new, relevant data (evidence). The Bayesian interpretation provides a standard set of procedur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a constant factor \lambda when the linear transformation is applied to it: T\mathbf v=\lambda \mathbf v. The corresponding eigenvalue, characteristic value, or characteristic root is the multiplying factor \lambda (possibly a negative or complex number). Geometrically, vectors are multi-dimensional quantities with magnitude and direction, often pictured as arrows. A linear transformation rotates, stretches, or shears the vectors upon which it acts. A linear transformation's eigenvectors are those vectors that are only stretched or shrunk, with neither rotation nor shear. The corresponding eigenvalue is the factor by which an eigenvector is stretched or shrunk. If the eigenvalue is negative, the eigenvector's direction is reversed. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (: matrices) is a rectangle, rectangular array or table of numbers, symbol (formal), symbols, or expression (mathematics), expressions, with elements or entries arranged in rows and columns, which is used to represent a mathematical object or property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two-by-three matrix", a " matrix", or a matrix of dimension . Matrices are commonly used in linear algebra, where they represent linear maps. In geometry, matrices are widely used for specifying and representing geometric transformations (for example rotation (mathematics), rotations) and coordinate changes. In numerical analysis, many computational problems are solved by reducing them to a matrix computation, and this often involves computing with matrices of huge dimensions. Matrices are used in most areas of mathematics and scientific fields, either directly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Test
Binomial test is an exact test of the statistical significance of deviations from a theoretically expected distribution of observations into two categories using sample data. Usage A binomial test is a statistical hypothesis test used to determine whether the proportion of successes in a sample differs from an expected proportion in a binomial distribution. It is useful for situations when there are two possible outcomes (e.g., success/failure, yes/no, heads/tails), i.e., where repeated experiments produce binary data. If one assumes an underlying probability \pi_0 between 0 and 1, the null hypothesis is : H_0\colon\pi=\pi_0 For a sample of size n, we would expect n\pi_0 successes. The formula of the binomial distribution gives the probability of those n samples instead producing k successes: : \Pr(X=k)=\binom\pi_0^k(1-\pi_0)^ Suppose that we want to test the alternative hypothesis : H_\colon\pi\pi_0 using the summation of the range from k to n instead. Calculating a p-val ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Q Methodology
Q methodology is a research method used in psychology and in social sciences to study people's "subjectivity"—that is, their viewpoint. Q was developed by psychologist William Stephenson. It has been used both in clinical settings for assessing a patient's progress over time (intra-rater comparison), as well as in research settings to examine how people think about a specific topic (inter-rater comparisons). Technical overview The name "Q" comes from the form of factor analysis that is used to analyze the data. Normal factor analysis, called "R method," involves finding correlations between variables (say, height and age) across a sample of subjects. Q, on the other hand, looks for correlations between subjects across a sample of variables. Q factor analysis reduces the many individual viewpoints of the subjects down to a few "factors," which are claimed to represent shared ways of thinking. It is sometimes said that Q factor analysis is R factor analysis with the data table t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
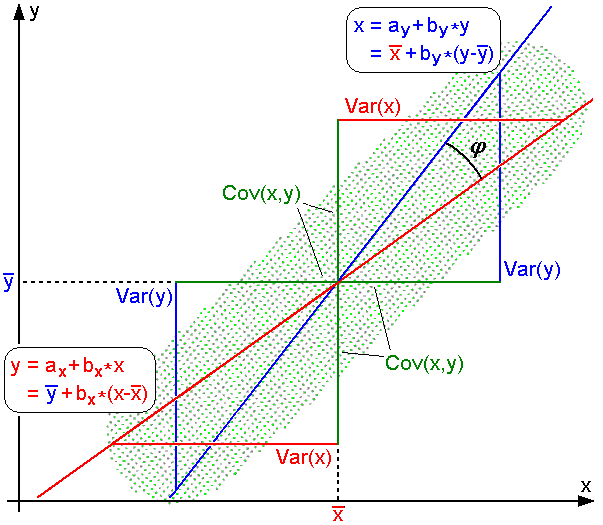
Pearson Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The nami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |