 |
Correlation Disattenuation
Regression dilution, also known as regression attenuation, is the biasing of the linear regression slope towards zero (the underestimation of its absolute value), caused by errors in the independent variable. Consider fitting a straight line for the relationship of an outcome variable ''y'' to a predictor variable ''x'', and estimating the slope of the line. Statistical variability, measurement error or random noise in the ''y'' variable causes uncertainty in the estimated slope, but not bias: on average, the procedure calculates the right slope. However, variability, measurement error or random noise in the ''x'' variable causes bias in the estimated slope (as well as imprecision). The greater the variance in the ''x'' measurement, the closer the estimated slope must approach zero instead of the true value. It may seem counter-intuitive that noise in the predictor variable ''x'' induces a bias, but noise in the outcome variable ''y'' does not. Recall that linear regression is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Visualization Of Errors-in-variables Linear Regression
Visualization or visualisation may refer to: *Visualization (graphics), the physical or imagining creation of images, diagrams, or animations to communicate a message * Data and information visualization, the practice of creating visual representations of complex data and information * Music visualization, animated imagery based on a piece of music *Mental image, the experience of images without the relevant external stimuli * "Visualization", a song by Blank Banshee on the 2012 album ''Blank Banshee 0'' See also * Creative visualization (other) * Visualizer (other) * * * * Graphics * List of graphical methods, various forms of visualization * Guided imagery, a mind-body intervention by a trained practitioner * Illustration, a decoration, interpretation or visual explanation of a text, concept or process * Image, an artifact that depicts visual perception, such as a photograph or other picture * Infographics {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Wayne Fuller
Wayne Arthur Fuller (born June 15, 1931) is an American statistician who has specialised in econometrics, survey sampling and time series analysis. He was on the staff of Iowa State University from 1959, becoming a Distinguished Professor in 1983. Fuller received his degrees from Iowa State University, with a B.S. in 1955, an M.S. in 1957 and a Ph.D. in Agricultural Economics in 1959. During his long career at Iowa State, he supervised 88 Ph.D. or M.S. dissertations. Fuller is a fellow of the American Statistical Association, the Econometric Society, the Institute of Mathematical Statistics, and the International Statistical Institute. Fuller also served as an editor of the American Journal of Agricultural Economics, Journal of the American Statistical Association, The American Statistician, Journal of Business and Economic Statistics, and Survey Methodology. He also served on numerous National Academy of Science panels and was a member of the Committee on National Statistics. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Pearson Correlation Coefficient
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The nami ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of statistical survey, surveys and experimental design, experiments. When census data (comprising every member of the target population) cannot be collected, statisticians collect data by developing specific experiment designs and survey sample (statistics), samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events. In other words, measurement is a process of determining how large or small a physical quantity is as compared to a basic reference quantity of the same kind. The scope and application of measurement are dependent on the context and discipline. In natural sciences and engineering, measurements do not apply to nominal properties of objects or events, which is consistent with the guidelines of the International Vocabulary of Metrology (VIM) published by the International Bureau of Weights and Measures (BIPM). However, in other fields such as statistics as well as the social and behavioural sciences, measurements can have multiple levels, which would include nominal, ordinal, interval and ratio scales. Measurement is a cornerstone of trade, science, technology and quantitative research in many disciplines. Historically, many measurement syste ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
The Science Of Mental Ability
''The g Factor: The Science of Mental Ability'' is a 1998 book by psychologist Arthur Jensen about the general factor of human mental ability, or ''g''. Summary The book traces the origins of the idea of individual differences in general mental ability to 19th century researchers Herbert Spencer and Francis Galton. Charles Spearman is credited for inventing factor analysis in the early 20th century, which enabled statistical testing of the hypothesis that general mental ability is required in all mental efforts. Spearman, gave the name ''g'' to the common factor underlying all mental tasks. He suggested that ''g'' reflected individual differences in "mental energy", and hoped that future research would uncover the biological basis of this energy.Jensen, A.R. (1999)The g Factor: the Science of Mental Ability. Precis of Jensen on Intelligence-g-Factor.''Psycoloquy: 10(023)'' The book argues that because it is difficult to arrive at a consensual scientific definition of the term ''i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Measurement Error
Observational error (or measurement error) is the difference between a measured value of a quantity and its unknown true value.Dodge, Y. (2003) ''The Oxford Dictionary of Statistical Terms'', OUP. Such errors are inherent in the measurement process; for example lengths measured with a ruler calibrated in whole centimeters will have a measurement error of several millimeters. The error or uncertainty of a measurement can be estimated, and is specified with the measurement as, for example, 32.3 ± 0.5 cm. Scientific observations are marred by two distinct types of errors, systematic errors on the one hand, and random, on the other hand. The effects of random errors can be mitigated by the repeated measurements. Constant or systematic errors on the contrary must be carefully avoided, because they arise from one or more causes which constantly act in the same way, and have the effect of always altering the result of the experiment in the same direction. They therefore alter the va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
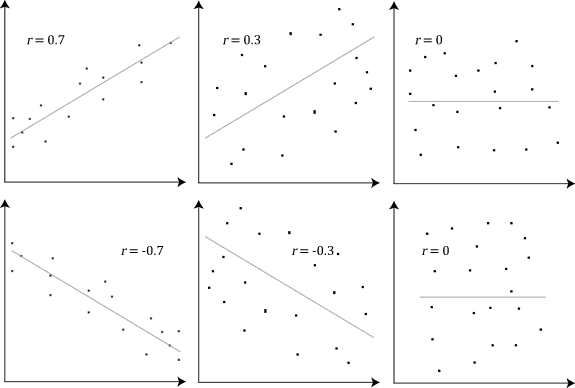 |
Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Charles Spearman
Charles Edward Spearman, FRS (10 September 1863 – 17 September 1945) was an English psychologist known for work in statistics, as a pioneer of factor analysis, and for Spearman's rank correlation coefficient. He also did seminal work on models for human intelligence, including his theory that disparate cognitive test scores reflect a single general intelligence factor and coining the term ''g'' factor. Biography Spearman had an unusual background for a psychologist. In his childhood he was ambitious to follow an academic career. But first he joined the army as a regular officer of engineers in August 1883, and was promoted to captain on 8 July 1893, serving in the Munster Fusiliers. After 15 years he resigned in 1897 to study for a PhD in experimental psychology. In Britain, psychology was generally seen as a branch of philosophy and Spearman chose to study in Leipzig under Wilhelm Wundt, because it was a centre of the "new psychology"—one that used the scientific met ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Survival Analysis
Survival analysis is a branch of statistics for analyzing the expected duration of time until one event occurs, such as death in biological organisms and failure in mechanical systems. This topic is called reliability theory, reliability analysis or reliability engineering in engineering, duration analysis or duration modelling in economics, and event history analysis in sociology. Survival analysis attempts to answer certain questions, such as what is the proportion of a population which will survive past a certain time? Of those that survive, at what rate will they die or fail? Can multiple causes of death or failure be taken into account? How do particular circumstances or characteristics increase or decrease the probability of survival? To answer such questions, it is necessary to define "lifetime". In the case of biological survival, death is unambiguous, but for mechanical reliability, failure may not be well-defined, for there may well be mechanical systems in which failure ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Proportional Hazards Models
Proportional hazards models are a class of survival models in statistics. Survival models relate the time that passes, before some event occurs, to one or more covariates that may be associated with that quantity of time. In a proportional hazards model, the unique effect of a unit increase in a covariate is multiplicative with respect to the hazard rate. The hazard rate at time t is the probability per short time d''t'' that an event will occur between t and t + dt given that up to time t no event has occurred yet. For example, taking a drug may halve one's hazard rate for a stroke occurring, or, changing the material from which a manufactured component is constructed, may double its hazard rate for failure. Other types of survival models such as accelerated failure time models do not exhibit proportional hazards. The accelerated failure time model describes a situation where the biological or mechanical life history of an event is accelerated (or decelerated). Background ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Correlated
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |