|
Coordinate Rotations And Reflections
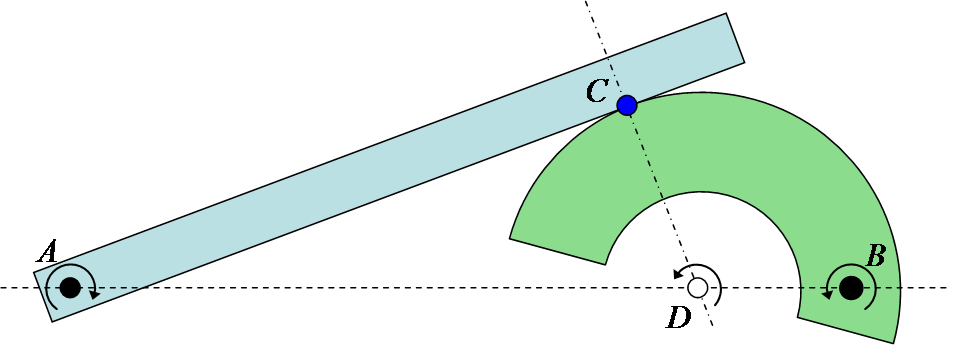
In Euclidean geometry, two-dimensional rotations and reflections are two kinds of Euclidean plane isometries which are related to one another. Process A rotation in the plane can be formed by composing a pair of reflections. First reflect a point to its image on the other side of line . Then reflect to its image on the other side of line . If lines and make an angle with one another, then points and will make an angle around point , the intersection of and . I.e., angle will measure . A pair of rotations about the same point will be equivalent to another rotation about point . On the other hand, the composition of a reflection and a rotation, or of a rotation and a reflection (composition is not commutative), will be equivalent to a reflection. Mathematical expression The statements above can be expressed more mathematically. Let a rotation about the origin by an angle be denoted as . Let a reflection about a line through the origin which makes an angle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry, ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms (postulates) and deducing many other propositions (theorems) from these. One of those is the parallel postulate which relates to parallel lines on a Euclidean plane. Although many of Euclid's results had been stated earlier,. Euclid was the first to organize these propositions into a logic, logical system in which each result is ''mathematical proof, proved'' from axioms and previously proved theorems. The ''Elements'' begins with plane geometry, still taught in secondary school (high school) as the first axiomatic system and the first examples of mathematical proofs. It goes on to the solid geometry of three dimensions. Much of the ''Elements'' states results of what are now called algebra and number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Group
In mathematics, the orthogonal group in dimension , denoted , is the Group (mathematics), group of isometry, distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by Function composition, composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrix, orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose invertible matrix, inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact group, compact. The orthogonal group in dimension has two connected component (topology), connected components. The one that contains the identity element is a normal subgroup, called the special orthogonal group, and denoted . It consists of all orthogonal matrices of determinant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Addison-Wesley
Addison–Wesley is an American publisher of textbooks and computer literature. It is an imprint of Pearson plc, a global publishing and education company. In addition to publishing books, Addison–Wesley also distributes its technical titles through the O'Reilly Online Learning e-reference service. Addison–Wesley's majority of sales derive from the United States (55%) and Europe (22%). The Addison–Wesley Professional Imprint produces content including books, eBooks, and video for the professional IT worker including developers, programmers, managers, system administrators. Classic titles include '' The Art of Computer Programming'', '' The C++ Programming Language'', '' The Mythical Man-Month'', and '' Design Patterns''. History Lew Addison Cummings and Melbourne Wesley Cummings founded Addison–Wesley in 1942, with the first book published by Addison–Wesley being Massachusetts Institute of Technology professor Francis Weston Sears' ''Mechanics''. Its first comput ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Houghton Mifflin Co
Houghton Mifflin Harcourt Company ( ; HMH) is an American publisher of textbooks, instructional technology materials, assessments, and reference works. The company is based in the Boston Financial District. It was formerly known as the Houghton Mifflin Company, but it changed its name following the 2007 acquisition of Harcourt Publishing. Prior to March 2010, it was a subsidiary of Education Media and Publishing Group Limited, an Irish-owned holding company registered in the Cayman Islands and formerly known as Riverdeep. In 2022, it was acquired by Veritas Capital, a New York-based private-equity firm. Company history In 1832, William Ticknor and John Allen purchased a bookselling business in Boston and began to involve themselves in publishing; James T. Fields joined as a partner in 1843. Fields and Ticknor gradually gathered an impressive list of writers, including Ralph Waldo Emerson, Nathaniel Hawthorne, and Henry David Thoreau. The duo formed a close relationship wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Wiley & Sons
John Wiley & Sons, Inc., commonly known as Wiley (), is an American Multinational corporation, multinational Publishing, publishing company that focuses on academic publishing and instructional materials. The company was founded in 1807 and produces books, Academic journal, journals, and encyclopedias, in print and electronically, as well as online products and services, training materials, and educational materials for undergraduate, graduate, and continuing education students. History The company was established in 1807 when Charles Wiley opened a print shop in Manhattan. The company was the publisher of 19th century American literary figures like James Fenimore Cooper, Washington Irving, Herman Melville, and Edgar Allan Poe, as well as of legal, religious, and other non-fiction titles. The firm took its current name in 1865. Wiley later shifted its focus to scientific, Technology, technical, and engineering subject areas, abandoning its literary interests. Wiley's son Joh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotation Group SO(3)
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space \R^3 under the operation of composition. By definition, a rotation about the origin is a transformation that preserves the origin, Euclidean distance (so it is an isometry), and orientation (i.e., ''handedness'' of space). Composing two rotations results in another rotation, every rotation has a unique inverse rotation, and the identity map satisfies the definition of a rotation. Owing to the above properties (along composite rotations' associative property), the set of all rotations is a group under composition. Every non-trivial rotation is determined by its axis of rotation (a line through the origin) and its angle of rotation. Rotations are not commutative (for example, rotating ''R'' 90° in the x-y plane followed by ''S'' 90° in the y-z plane is not the same as ''S'' followed by ''R''), making the 3D rotation grou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthogonal Group
In mathematics, the orthogonal group in dimension , denoted , is the Group (mathematics), group of isometry, distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by Function composition, composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrix, orthogonal matrices, where the group operation is given by matrix multiplication (an orthogonal matrix is a real matrix whose invertible matrix, inverse equals its transpose). The orthogonal group is an algebraic group and a Lie group. It is compact group, compact. The orthogonal group in dimension has two connected component (topology), connected components. The one that contains the identity element is a normal subgroup, called the special orthogonal group, and denoted . It consists of all orthogonal matrices of determinant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Instant Centre Of Rotation
The instant center of rotation (also known as instantaneous velocity center, instantaneous center, or pole of planar displacement) of a body undergoing planar movement is a point that has zero velocity at a particular instant of time. At this instant, the velocity vectors of the other points in the body generate a circular field around this center of rotation which is identical to what is generated by a pure rotation. Planar movement of a body is often described using a plane figure moving in a two-dimensional plane. The instant center is the point in the moving plane around which all other points are rotating at a specific instant of time. The continuous movement of a plane has an instant center for every value of the time parameter. This generates a curve called the moving centrode. The points in the fixed plane corresponding to these instant centers form the fixed centrode. The generalization of this concept to 3-dimensional space is that of a twist around a screw. The sc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Symmetries
In geometry, an object has symmetry if there is an Operation (mathematics), operation or Transformation (function), transformation (such as Translation (geometry), translation, Scaling (geometry), scaling, Rotation (mathematics), rotation or Reflection (mathematics), reflection) that maps the figure/object onto itself (i.e., the object has an Invariant (mathematics), invariance under the transform). Thus, a symmetry can be thought of as an immunity to change. For instance, a circle rotated about its center will have the same shape and size as the original circle, as all points before and after the transform would be indistinguishable. A circle is thus said to be ''symmetric under rotation'' or to have ''rotational symmetry''. If the isometry is the reflection of a plane figure about a line, then the figure is said to have reflectional symmetry or line symmetry; it is also possible for a figure/object to have more than one line of symmetry. The types of symmetries that are possible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dihedral Group
In mathematics, a dihedral group is the group (mathematics), group of symmetry, symmetries of a regular polygon, which includes rotational symmetry, rotations and reflection symmetry, reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry. The notation for the dihedral group differs in geometry and abstract algebra. In geometry, or refers to the symmetries of the n-gon, -gon, a group of order . In abstract algebra, refers to this same dihedral group. This article uses the geometric convention, . Definition The word "dihedral" comes from "di-" and "-hedron". The latter comes from the Greek word hédra, which means "face of a geometrical solid". Overall it thus refers to the two faces of a polygon. Elements A regular polygon with n sides has 2n different symmetries: n rotational symmetry, rotational symmetries and n reflection symmetry, reflection symmetries. Usually, we take n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Clockwise
Two-dimensional rotation can occur in two possible directions or senses of rotation. Clockwise motion (abbreviated CW) proceeds in the same direction as a clock's hands relative to the observer: from the top to the right, then down and then to the left, and back up to the top. The opposite sense of rotation or revolution is (in Commonwealth English) anticlockwise (ACW) or (in North American English) counterclockwise (CCW). Three-dimensional rotation can have similarly defined senses when considering the corresponding angular velocity vector. Terminology Before clocks were commonplace, the terms " sunwise" and "deasil", "deiseil" and even "deocil" from the Scottish Gaelic language and from the same root as the Latin "dexter" ("right") were used for clockwise. " Widdershins" or "withershins" (from Middle Low German "weddersinnes", "opposite course") was used for counterclockwise. The terms clockwise and counterclockwise can only be applied to a rotational motion once a side ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |