|
Conditional Variance Swap
A conditional variance swap is a type of variance swap or swap derivative product that allows investors to take exposure to volatility in the price of an underlying security but only while the underlying security is within a pre-specified price range. This instrument can be useful for hedging complex volatility exposures, making a bet on the volatility levels contained in the skew of the underlying security's price, or buying/selling variance at more attractive levels given a view on the underlying security.Allen, Peter; Einchcomb, Stephen, and Granger, Nicolas. ''Conditional Variance Swaps: Product Note''. JPMorgan, 3 April 2006. History Regular variance swap were introduced first, and became a popular instrument for hedging against the effect of volatility on option prices. Thus, the market for these securities became increasingly liquid, and pricing for these swaps became more efficient. However, investors noticed that to a certain extent the price levels for these variance ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Variance Swap
A variance swap is an over-the-counter financial derivative that allows one to speculate on or hedge risks associated with the magnitude of movement, i.e. volatility, of some underlying product, like an exchange rate, interest rate, or stock index. One leg of the swap will pay an amount based upon the realized variance of the price changes of the underlying product. Conventionally, these price changes will be daily log returns, based upon the most commonly used closing price. The other leg of the swap will pay a fixed amount, which is the strike, quoted at the deal's inception. Thus the net payoff to the counterparties will be the difference between these two and will be settled in cash at the expiration of the deal, though some cash payments will likely be made along the way by one or the other counterparty to maintain agreed upon margin. Structure and features The features of a variance swap include: * the variance strike * the realized variance * the vega notional: Like ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Swap (finance)
In finance, a swap is an agreement between two counterparties to exchange financial instruments, cashflows, or payments for a certain time. The instruments can be almost anything but most swaps involve cash based on a notional principal amount.Financial Industry Business Ontology Version 2 Annex D: Derivatives, EDM Council, Inc., Object Management Group, Inc., 2019 The general swap can also be seen as a series of forward contracts through which two parties exchange financial instruments, resulting in a common series of exchange dates and two streams of instruments, the ''legs'' of the swap. The legs can be almost anything but usually one leg involves cash flows based on a [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative (finance)
In finance, a derivative is a contract that ''derives'' its value from the performance of an underlying entity. This underlying entity can be an asset, Index fund, index, or interest rate, and is often simply called the "underlying". Derivatives can be used for a number of purposes, including insuring against price movements (Hedge (finance)#Etymology, hedging), increasing exposure to price movements for speculation, or getting access to otherwise hard-to-trade assets or markets. Some of the more common derivatives include Forward contract, forwards, Futures contract, futures, Option (finance), options, Swap (finance), swaps, and variations of these such as synthetic collateralized debt obligations and credit default swaps. Most derivatives are traded over-the-counter (finance), over-the-counter (off-exchange) or on an exchange such as the Chicago Mercantile Exchange, while most insurance contracts have developed into a separate industry. In the United States, after the financia ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
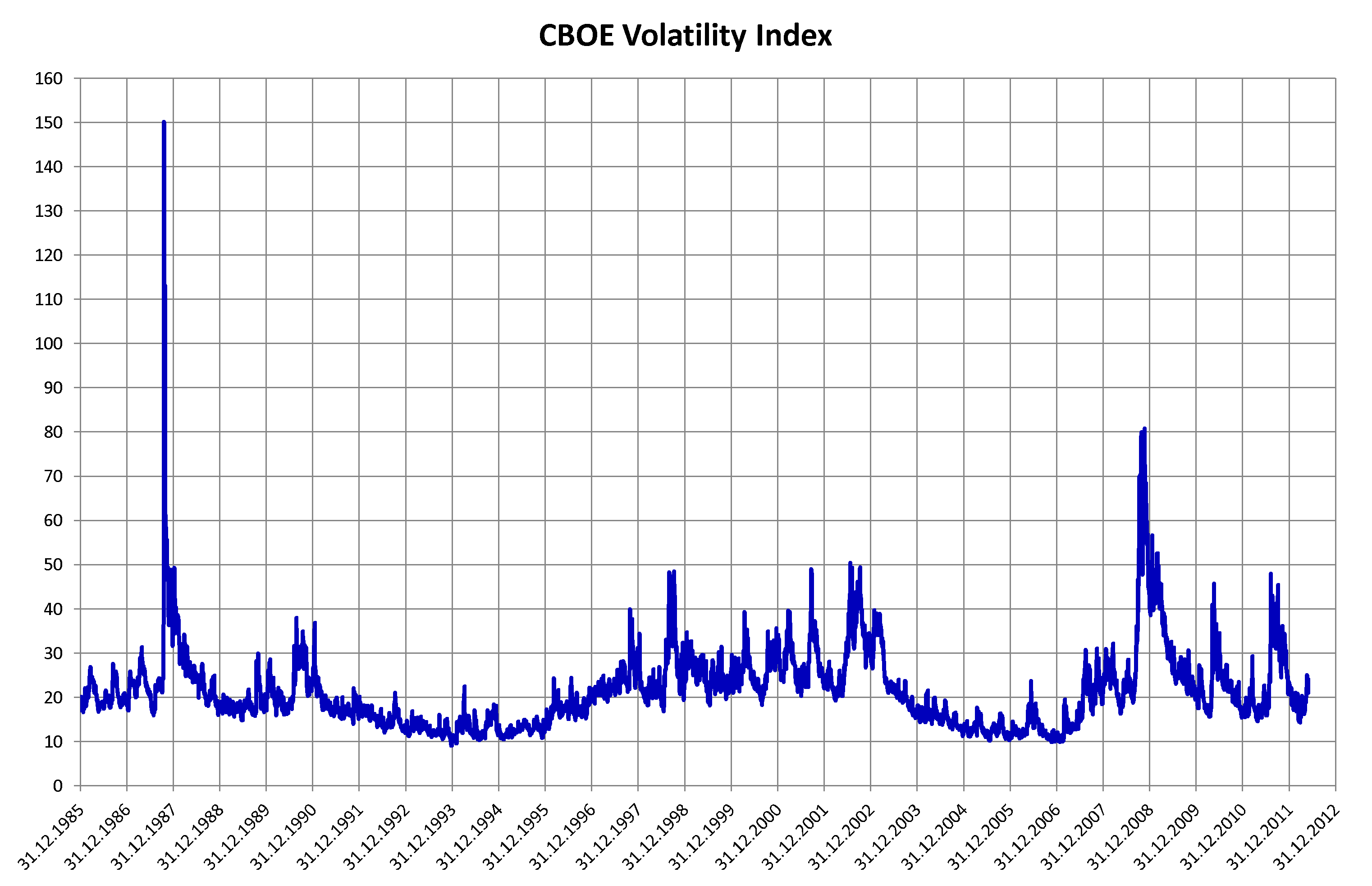
Volatility (finance)
In finance, volatility (usually denoted by ''σ'') is the degree of variation of a trading price series over time, usually measured by the standard deviation of logarithmic returns. Historic volatility measures a time series of past market prices. Implied volatility looks forward in time, being derived from the market price of a market-traded derivative (in particular, an option). Volatility terminology Volatility as described here refers to the actual volatility, more specifically: * actual current volatility of a financial instrument for a specified period (for example 30 days or 90 days), based on historical prices over the specified period with the last observation the most recent price. * actual historical volatility which refers to the volatility of a financial instrument over a specified period but with the last observation on a date in the past **near synonymous is realized volatility, the square root of the realized variance, in turn calculated using the sum of s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution, negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution, but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Introduction Consider the two distributions in the figure just below. Within each graph, the values on the right side of the distribution taper differently from the values on the left side. These tapering sides are called ' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Black–Scholes Model
The Black–Scholes or Black–Scholes–Merton model is a mathematical model for the dynamics of a financial market containing derivative investment instruments. From the parabolic partial differential equation in the model, known as the Black–Scholes equation, one can deduce the Black–Scholes formula, which gives a theoretical estimate of the price of European-style options and shows that the option has a ''unique'' price given the risk of the security and its expected return (instead replacing the security's expected return with the risk-neutral rate). The equation and model are named after economists Fischer Black and Myron Scholes; Robert C. Merton, who first wrote an academic paper on the subject, is sometimes also credited. The main principle behind the model is to hedge the option by buying and selling the underlying asset in a specific way to eliminate risk. This type of hedging is called "continuously revised delta hedging" and is the basis of more complicated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Replicating Portfolio
In mathematical finance, a replicating portfolio for a given asset or series of cash flows is a portfolio of assets with the same properties (especially cash flows). This is meant in two distinct senses: static replication, where the portfolio has the same cash flows as the reference asset (and no changes need to be made to maintain this), and dynamic replication, where the portfolio does not have the same cash flows, but has the same "Greeks" as the reference asset, meaning that for small (properly, infinitesimal) changes to underlying market parameters, the price of the asset and the price of the portfolio change in the same way. Dynamic replication requires continual adjustment, as the asset and portfolio are only assumed to behave similarly at a single point (mathematically, their partial derivatives are equal at a single point). Given an asset or liability, an offsetting replicating portfolio (a "hedge") is called a static hedge or dynamic hedge, and constructing such a portfol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Out-of-the-money
In finance, moneyness is the relative position of the current price (or future price) of an underlying asset (e.g., a stock) with respect to the strike price of a derivative, most commonly a call option or a put option. Moneyness is firstly a three-fold classification: * If the derivative would have positive intrinsic value if it were to expire today, it is said to be in the money; * If the derivative would be worthless if expiring with the underlying at its current price, it is said to be out of the money; * And if the current underlying price and strike price are equal, the derivative is said to be at the money. There are two slightly different definitions, according to whether one uses the current price (spot) or future price (forward), specified as "at the money spot" or "at the money forward", etc. This rough classification can be quantified by various definitions to express the moneyness as a number, measuring how far the asset is in the money or out of the money with re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivatives (finance)
The derivative of a function is the rate of change of the function's output relative to its input value. Derivative may also refer to: In mathematics and economics * Brzozowski derivative in the theory of formal languages * Formal derivative, an operation on elements of a polynomial ring which mimics the form of the derivative from calculus * Radon–Nikodym derivative in measure theory * Derivative (set theory), a concept applicable to normal functions * Derivative (graph theory), an alternative term for a line graph deva *Derivative (finance), a contract whose value is derived from that of other quantities * Derivative suit or derivative action, a type of lawsuit filed by shareholders of a corporation In science and engineering *Derivative (chemistry), a type of compound which is a product of the process of derivatization * Derivative (linguistics), the process of forming a new word on the basis of an existing word, e.g. happiness and unhappy from happy *Aeroderivative gas turb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |