|
Coefficient Of Colligation
In statistics, Yule's ''Y'', also known as the coefficient of colligation, is a measure of association between two binary variables. The measure was developed by George Udny Yule in 1912,Michel G. Soete. A new theory on the measurement of association between two binary variables in medical sciences: association can be expressed in a fraction (per unum, percentage, pro mille....) of perfect association (2013), e-article, BoekBoek.be and should not be confused with Yule's coefficient for measuring skewness based on quartiles. Formula For a 2×2 table for binary variables ''U'' and ''V'' with frequencies or proportions : Yule's ''Y'' is given by :Y = \frac. Yule's ''Y'' is closely related to the odds ratio ''OR'' = ''ad''/(''bc'') as is seen in following formula: :Y = \frac Yule's ''Y'' varies from −1 to +1. −1 reflects total negative correlation, +1 reflects perfect positive association while 0 reflects no association at all. These correspond to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
George Udny Yule
George Udny Yule, CBE, FRS (18 February 1871 – 26 June 1951), usually known as Udny Yule, was a British statistician, particularly known for the Yule distribution and proposing the preferential attachment model for random graphs. Personal life Yule was born at Beech Hill, a house in Morham near Haddington, Scotland and died in Cambridge, England. He came from a Scottish family composed of army officers, civil servants, scholars, and administrators. His father, Sir George Udny Yule (1813–1886) was a brother of the noted orientalist Sir Henry Yule (1820–1889). His great-uncle was the botanist John Yule. In 1899, Yule married May Winifred Cummings. The marriage was annulled in 1912, producing no children.annulment: Yates, 1952 Education and teaching Udny Yule was educated at Winchester College and at the age of 16 at University College London where he read engineering. After a year in Bonn doing research in experimental physics under Heinrich Rudolf Hertz, Yule r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skewness
In probability theory and statistics, skewness is a measure of the asymmetry of the probability distribution of a real-valued random variable about its mean. The skewness value can be positive, zero, negative, or undefined. For a unimodal distribution (a distribution with a single peak), negative skew commonly indicates that the ''tail'' is on the left side of the distribution, and positive skew indicates that the tail is on the right. In cases where one tail is long but the other tail is fat, skewness does not obey a simple rule. For example, a zero value in skewness means that the tails on both sides of the mean balance out overall; this is the case for a symmetric distribution but can also be true for an asymmetric distribution where one tail is long and thin, and the other is short but fat. Thus, the judgement on the symmetry of a given distribution by using only its skewness is risky; the distribution shape must be taken into account. Introduction Consider the two d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quartiles
In statistics, quartiles are a type of quantiles which divide the number of data points into four parts, or ''quarters'', of more-or-less equal size. The data must be ordered from smallest to largest to compute quartiles; as such, quartiles are a form of order statistic. The three quartiles, resulting in four data divisions, are as follows: * The first quartile (''Q''1) is defined as the 25th percentile where lowest 25% data is below this point. It is also known as the ''lower'' quartile. * The second quartile (''Q''2) is the median of a data set; thus 50% of the data lies below this point. * The third quartile (''Q''3) is the 75th percentile where lowest 75% data is below this point. It is known as the ''upper'' quartile, as 75% of the data lies below this point. Along with the minimum and maximum of the data (which are also quartiles), the three quartiles described above provide a five-number summary of the data. This summary is important in statistics because it provides inform ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Variable
Binary data is data whose unit can take on only two possible states. These are often labelled as 0 and 1 in accordance with the binary numeral system and Boolean algebra. Binary data occurs in many different technical and scientific fields, where it can be called by different names including '' bit'' (binary digit) in computer science, ''truth value'' in mathematical logic and related domains and '' binary variable'' in statistics. Mathematical and combinatoric foundations A discrete variable that can take only one state contains zero information, and is the next natural number after 1. That is why the bit, a variable with only two possible values, is a standard primary unit of information. A collection of bits may have states: see binary number for details. Number of states of a collection of discrete variables depends exponentially on the number of variables, and only as a power law on number of states of each variable. Ten bits have more () states than three decimal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Odds Ratio
An odds ratio (OR) is a statistic that quantifies the strength of the association between two events, A and B. The odds ratio is defined as the ratio of the odds of event A taking place in the presence of B, and the odds of A in the absence of B. Due to symmetry, odds ratio reciprocally calculates the ratio of the odds of B occurring in the presence of A, and the odds of B in the absence of A. Two events are independent if and only if the OR equals 1, i.e., the odds of one event are the same in either the presence or absence of the other event. If the OR is greater than 1, then A and B are associated (correlated) in the sense that, compared to the absence of B, the presence of B raises the odds of A, and symmetrically the presence of A raises the odds of B. Conversely, if the OR is less than 1, then A and B are negatively correlated, and the presence of one event reduces the odds of the other event occurring. Note that the odds ratio is symmetric in the two events, and no causa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
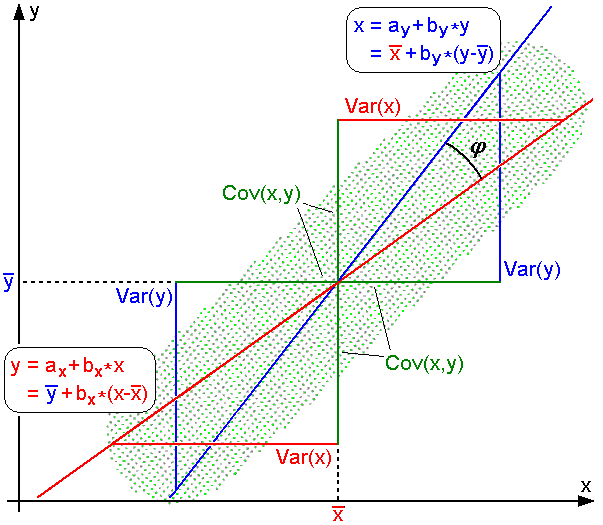
Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics it usually refers to the degree to which a pair of variables are '' linearly'' related. Familiar examples of dependent phenomena include the correlation between the height of parents and their offspring, and the correlation between the price of a good and the quantity the consumers are willing to purchase, as it is depicted in the demand curve. Correlations are useful because they can indicate a predictive relationship that can be exploited in practice. For example, an electrical utility may produce less power on a mild day based on the correlation between electricity demand and weather. In this example, there is a causal relationship, because extreme weather causes people to use more electricity for heating or cooling. However, in g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pearson Correlation
In statistics, the Pearson correlation coefficient (PCC) is a correlation coefficient that measures linear correlation between two sets of data. It is the ratio between the covariance of two variables and the product of their standard deviations; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation). Naming and history It was developed by Karl Pearson from a related idea introduced by Francis Galton in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The namin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yule's Q
In statistics Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ..., Goodman and Kruskal's gamma is a measure of rank correlation, i.e., the similarity of the orderings of the data when ranked by each of the quantities. It measures the strength of association of the cross tabulated data when both variables are measured at the ordinal level. It makes no adjustment for either table size or ties. Values range from −1 (100% negative association, or perfect inversion) to +1 (100% positive association, or perfect agreement). A value of zero indicates the absence of association. This statistic (which is distinct from Goodman and Kruskal's lambda) is named after Leo Goodman and William Kruskal, who proposed it in a series of papers from 1954 to 1972. Definition The estimate of gamm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unum (number Format)
Unums (''universal numbers'') are a family of number formats and arithmetic for implementing real numbers on a computer, proposed by John L. Gustafson in 2015. They are designed as an alternative to the ubiquitous IEEE 754 floating-point standard. The latest version is known as ''posits''. Type I Unum The first version of unums, formally known as Type I unum, was introduced in Gustafson's book ''The End of Error'' as a superset of the IEEE-754 floating-point format. The defining features of the Type I unum format are: * a variable-width storage format for both the significand and exponent, and * a ''u-bit'', which determines whether the unum corresponds to an exact number (''u'' = 0), or an interval between consecutive exact unums (''u'' = 1). In this way, the unums cover the entire extended real number line ��∞,+∞ For computation with the format, Gustafson proposed using interval arithmetic with a pair of unums, what he called a ''ubound'', provid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |