|
Cauchy–Born Rule
The Cauchy–Born rule or Cauchy–Born approximation is a basic hypothesis used in the mathematical formulation of solid mechanics which relates the movement of atoms in a crystal to the overall deformation of the bulk solid. A widespread simplified version states that in a crystalline solid subject to a small strain, the positions of the atoms within the crystal lattice follow the overall strain of the medium. The rule first appears in Max Born and Huang Kun's ''Dynamical Theory of Crystal Lattices'', a refinement of Augustin-Louis Cauchy's relations which were used to derive the equations satisfied by the Cauchy stress tensor. Description To give a more precise definition, consider a crystalline body where the position of the atoms can be described by a set of reference lattice vectors \mathbf^0. The Cauchy–Born rules states that if the body is deformed by a deformation whose gradient is \mathbf, the lattice of the deform body can be described by \mathbf = \mathbf \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Born Rule
The Born rule is a postulate of quantum mechanics that gives the probability that a measurement of a quantum system will yield a given result. In one commonly used application, it states that the probability density for finding a particle at a given position is proportional to the square of the amplitude of the system's wavefunction at that position. It was formulated and published by German physicist Max Born in July 1926. Details The Born rule states that an observable, measured in a system with normalized wave function , \psi\rang (see Bra–ket notation), corresponds to a self-adjoint operator A whose spectrum is discrete if: * the measured result will be one of the eigenvalues \lambda of A, and * the probability of measuring a given eigenvalue \lambda_i will equal \lang\psi, P_i, \psi\rang, where P_i is the projection onto the eigenspace of A corresponding to \lambda_i. : (In the case where the eigenspace of A corresponding to \lambda_i is one-dimensional and spanned by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lattice (group)
In geometry and group theory, a lattice in the real coordinate space \mathbb^n is an infinite set of points in this space with the properties that coordinate-wise addition or subtraction of two points in the lattice produces another lattice point, that the lattice points are all separated by some minimum distance, and that every point in the space is within some maximum distance of a lattice point. Closure under addition and subtraction means that a lattice must be a subgroup of the additive group of the points in the space, and the requirements of minimum and maximum distance can be summarized by saying that a lattice is a Delone set. More abstractly, a lattice can be described as a free abelian group of dimension n which spans the vector space \mathbb^n. For any basis of \mathbb^n, the subgroup of all linear combinations with integer coefficients of the basis vectors forms a lattice, and every lattice can be formed from a basis in this way. A lattice may be viewed as a re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Born–Huang Approximation
The Born–Huang approximation is an approximation closely related to the Born–Oppenheimer approximation. It takes into account diagonal nonadiabatic effects in the electronic Hamiltonian better than the Born–Oppenheimer approximation. Despite the addition of correction terms, the electronic states remain uncoupled under the Born–Huang approximation, making it an adiabatic approximation. The approximation is named after Max Born and Huang Kun who wrote about it in the ''Dynamical Theory of Crystal Lattices''. Shape The Born–Huang approximation asserts that the representation matrix of nuclear kinetic energy operator in the basis of Born–Oppenheimer electronic wavefunctions is diagonal: : \langle\chi_(\mathbf; \mathbf) , T_\mathrm , \chi_k(\mathbf; \mathbf)\rangle_ = \mathcal_\mathrm(\mathbf)\delta_. Consequences The Born–Huang approximation loosens the Born–Oppenheimer approximation by including some electronic matrix elements, while at the same ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ted Belytschko
Ted Bohdan Belytschko (January 13, 1943 – September 15, 2014) was an American mechanical engineer. He was Walter P. Murphy Professor and McCormick Professor of Computational Mechanics at Northwestern University. He worked in the field of computational solid mechanics and was known for development of methods like element-free Galerkin method and the Extended finite element method. Belytschko received his B.S. in Engineering Sciences (1965) and his Ph.D. in Mechanics (1968) from the Illinois Institute of Technology. He was named in ISI Database as the fourth most cited engineering researcher in January 2004. He was also the editor of the ''International Journal for Numerical Methods in Engineering''. He died at the age of 71 on September 15, 2014. Awards and honors * William Prager Medal, 2011. *Member of the National Academy of Sciences (2011) *Member of the National Academy of Engineering (1992) * John von Neumann Medal of the United States Association for Computational Mech ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stress–strain Curve
In engineering and materials science, a stress–strain curve for a material gives the relationship between stress and strain. It is obtained by gradually applying load to a test coupon and measuring the deformation, from which the stress and strain can be determined (see tensile testing). These curves reveal many of the properties of a material, such as the Young's modulus, the yield strength and the ultimate tensile strength. Definition Generally speaking, curves that represent the relationship between stress and strain in any form of deformation can be regarded as stress–strain curves. The stress and strain can be normal, shear, or a mixture, and can also be uniaxial, biaxial, or multiaxial, and can even change with time. The form of deformation can be compression, stretching, torsion, rotation, and so on. If not mentioned otherwise, stress–strain curve typically refers to the relationship between axial normal stress and axial normal strain of materials measur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
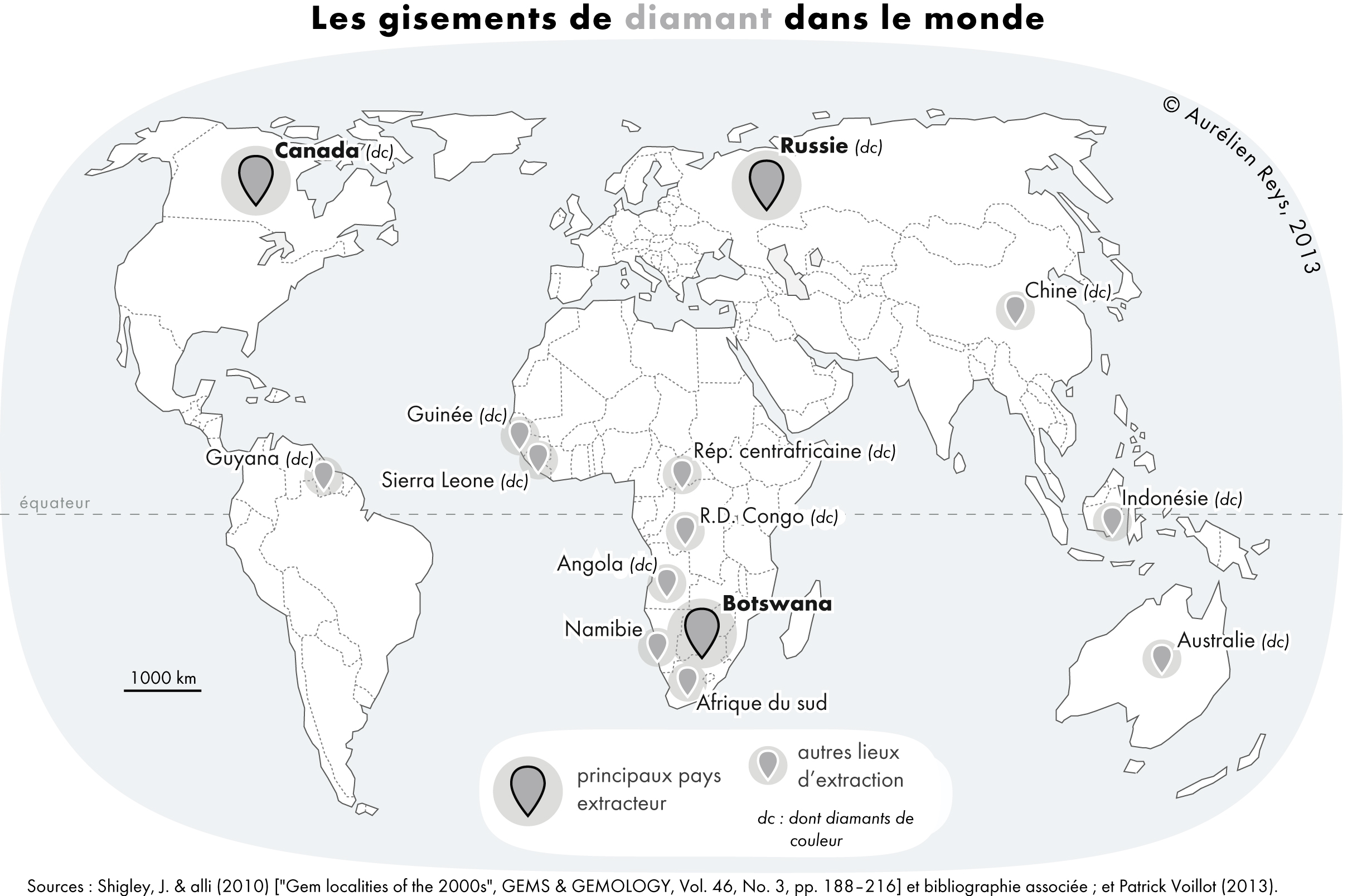
Diamond
Diamond is a Allotropes of carbon, solid form of the element carbon with its atoms arranged in a crystal structure called diamond cubic. Diamond is tasteless, odourless, strong, brittle solid, colourless in pure form, a poor conductor of electricity, and insoluble in water. Another solid form of carbon known as graphite is the Chemical stability, chemically stable form of carbon at Standard temperature and pressure, room temperature and pressure, but diamond is metastable and converts to it at a negligible rate under those conditions. Diamond has the highest Scratch hardness, hardness and thermal conductivity of any natural material, properties that are used in major industrial applications such as cutting and polishing tools. Because the arrangement of atoms in diamond is extremely rigid, few types of impurity can contaminate it (two exceptions are boron and nitrogen). Small numbers of lattice defect, defects or impurities (about one per million of lattice atoms) can color ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cubic Crystal System
In crystallography, the cubic (or isometric) crystal system is a crystal system where the unit cell is in the shape of a cube. This is one of the most common and simplest shapes found in crystals and minerals. There are three main varieties of these crystals: *Primitive cubic (abbreviated ''cP'' and alternatively called simple cubic) *Body-centered cubic (abbreviated ''cI'' or bcc) *Face-centered cubic (abbreviated ''cF'' or fcc) Note: the term fcc is often used in synonym for the ''cubic close-packed'' or ccp structure occurring in metals. However, fcc stands for a face-centered cubic Bravais lattice, which is not necessarily close-packed when a motif is set onto the lattice points. E.g. the diamond and the zincblende lattices are fcc but not close-packed. Each is subdivided into other variants listed below. Although the ''unit cells'' in these crystals are conventionally taken to be cubes, the primitive unit cells often are not. Bravais lattices The three Bravais latices ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Strain Theory
In continuum mechanics, the finite strain theory—also called large strain theory, or large deformation theory—deals with deformations in which strains and/or rotations are large enough to invalidate assumptions inherent in infinitesimal strain theory. In this case, the undeformed and deformed configurations of the continuum are significantly different, requiring a clear distinction between them. This is commonly the case with elastomers, plastically deforming materials and other fluids and biological soft tissue. Displacement field Deformation gradient tensor The deformation gradient tensor \mathbf F(\mathbf X,t) = F_ \mathbf e_j \otimes \mathbf I_K is related to both the reference and current configuration, as seen by the unit vectors \mathbf e_j and \mathbf I_K\,\!, therefore it is a '' two-point tensor''. Two types of deformation gradient tensor may be defined. Due to the assumption of continuity of \chi(\mathbf X,t)\,\!, \mathbf F has the inverse \mathbf H = \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy Stress Tensor
In continuum mechanics, the Cauchy stress tensor (symbol \boldsymbol\sigma, named after Augustin-Louis Cauchy), also called true stress tensor or simply stress tensor, completely defines the state of stress at a point inside a material in the deformed state, placement, or configuration. The second order tensor consists of nine components \sigma_ and relates a unit-length direction vector e to the ''traction vector'' T(e) across an imaginary surface perpendicular to e: :\mathbf^ = \mathbf e \cdot\boldsymbol\quad \text \quad T_^= \sum_\sigma_e_i. The SI base units of both stress tensor and traction vector are newton per square metre (N/m2) or pascal (Pa), corresponding to the stress scalar. The unit vector is dimensionless. The Cauchy stress tensor obeys the tensor transformation law under a change in the system of coordinates. A graphical representation of this transformation law is the Mohr's circle for stress. The Cauchy stress tensor is used for stress analysis of mater ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is the foundation of all quantum physics, which includes quantum chemistry, quantum field theory, quantum technology, and quantum information science. Quantum mechanics can describe many systems that classical physics cannot. Classical physics can describe many aspects of nature at an ordinary (macroscopic and Microscopic scale, (optical) microscopic) scale, but is not sufficient for describing them at very small submicroscopic (atomic and subatomic) scales. Classical mechanics can be derived from quantum mechanics as an approximation that is valid at ordinary scales. Quantum systems have Bound state, bound states that are Quantization (physics), quantized to Discrete mathematics, discrete values of energy, momentum, angular momentum, and ot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Augustin-Louis Cauchy
Baron Augustin-Louis Cauchy ( , , ; ; 21 August 1789 – 23 May 1857) was a French mathematician, engineer, and physicist. He was one of the first to rigorously state and prove the key theorems of calculus (thereby creating real analysis), pioneered the field complex analysis, and the study of permutation groups in abstract algebra. Cauchy also contributed to a number of topics in mathematical physics, notably continuum mechanics. A profound mathematician, Cauchy had a great influence over his contemporaries and successors; Hans Freudenthal stated: : "More concepts and theorems have been named for Cauchy than for any other mathematician (in elasticity alone there are sixteen concepts and theorems named for Cauchy)." Cauchy was a prolific worker; he wrote approximately eight hundred research articles and five complete textbooks on a variety of topics in the fields of mathematics and mathematical physics. Biography Youth and education Cauchy was the son of Lou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Theory Of Crystal Lattices
''Dynamical Theory of Crystal Lattices'' is a book in solid state physics, authored collaboratively by Max Born and Kun Huang. The book was originally started by Born in c. 1940, and was finished in the 1950s by Huang in consultation with Born. The text is considered a classical treatise on the subject of lattice dynamics, phonon theory, and elasticity in crystalline solids, but excluding metals and other complex solids with order/disorder phenomena. J. D. Eshelby, Melvin Lax, and A. J. C. Wilson reviewed the book in 1955, among several others. The book introduces the concept of Cauchy–Born rule and Born–Huang approximation. See also * Bibliography of Max Born * ''Introduction to Solid State Physics ''Introduction to Solid State Physics'', known colloquially as ''Kittel'', is a classic condensed matter physics textbook written by American physicist Charles Kittel in 1953. The book has been highly influential and has seen widespread adoptio ...'' References E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |