|
Born–Huang Approximation
The Born–Huang approximation is an approximation closely related to the Born–Oppenheimer approximation. It takes into account diagonal nonadiabatic effects in the electronic Hamiltonian better than the Born–Oppenheimer approximation. Despite the addition of correction terms, the electronic states remain uncoupled under the Born–Huang approximation, making it an adiabatic approximation. The approximation is named after Max Born and Huang Kun who wrote about it in the ''Dynamical Theory of Crystal Lattices''. Shape The Born–Huang approximation asserts that the representation matrix of nuclear kinetic energy operator in the basis of Born–Oppenheimer electronic wavefunctions is diagonal: : \langle\chi_(\mathbf; \mathbf) , T_\mathrm , \chi_k(\mathbf; \mathbf)\rangle_ = \mathcal_\mathrm(\mathbf)\delta_. Consequences The Born–Huang approximation loosens the Born–Oppenheimer approximation by including some electronic matrix elements, while at the same ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Born–Oppenheimer Approximation
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense ferment in the development of quantum mechanics. The approximation is widely used in quantum chemistry to speed up the computation of molecular wavefunctions and other properties for large molecules. There are cases where the assumption of separable motion no longer holds, which make the approximation lose validity (it is said to "break down"), but even then the app ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian (quantum Mechanics)
In quantum mechanics, the Hamiltonian of a system is an operator corresponding to the total energy of that system, including both kinetic energy and potential energy. Its spectrum, the system's ''energy spectrum'' or its set of ''energy eigenvalues'', is the set of possible outcomes obtainable from a measurement of the system's total energy. Due to its close relation to the energy spectrum and time-evolution of a system, it is of fundamental importance in most formulations of quantum theory. The Hamiltonian is named after William Rowan Hamilton, who developed a revolutionary reformulation of Newtonian mechanics, known as Hamiltonian mechanics, which was historically important to the development of quantum physics. Similar to vector notation, it is typically denoted by \hat, where the hat indicates that it is an operator. It can also be written as H or \check. Introduction The Hamiltonian of a system represents the total energy of the system; that is, the sum of the kine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electronic State
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized. In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's nucleus. The closest shell to the nucleus is called the "1 shell" (also called "K shell"), followed by the "2 shell" (or "L shell"), then the "3 shell" (or "M shell"), and so on further and further from the nucleus. The shells correspond with the principa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Max Born
Max Born (; 11 December 1882 – 5 January 1970) was a German-British theoretical physicist who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics, and supervised the work of a number of notable physicists in the 1920s and 1930s. Born shared the 1954 Nobel Prize in Physics with Walther Bothe "for his fundamental research in quantum mechanics, especially in the statistical interpretation of the wave function". Born entered the University of Göttingen in 1904, where he met the three renowned mathematicians Felix Klein, David Hilbert, and Hermann Minkowski. He wrote his PhD thesis on the subject of the stability of elastic wires and tapes, winning the university's Philosophy Faculty Prize. In 1905, he began researching special relativity with Minkowski, and subsequently wrote his habilitation thesis on the Thomson model of the atom. A chance meeting with Fritz Haber in Berlin in 1918 led to discussion of how an io ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Huang Kun
Huang Kun (; September 2, 1919 – July 6, 2005) was a Chinese physicist and an academician of the Chinese Academy of Sciences. He was awarded the State Preeminent Science and Technology Award (the highest science award in China) by President Jiang Zemin in 2001. Born in Beijing, China, in 1919, Huang graduated from Yenching University with a degree in physics. In 1948, he earned his PhD from the H. H. Wills Physics Lab of Bristol University in England and continued his postdoctoral studies at Liverpool University, where he coauthored the book '' Dynamical Theory of Crystal Lattices'' with Max Born between 1949 and 1951. The book has become a classic work of modern physics. The Born–Huang approximation is named after them. In 1951, Huang returned to China to teach, and became a professor of physics at Peking University. In 1955, he became a founding member of the Chinese Academy of Sciences (CAS). After his retirement in 1983, Huang remained active in the research of semicon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dynamical Theory Of Crystal Lattices
''Dynamical Theory of Crystal Lattices'' is a book in solid state physics, authored collaboratively by Max Born and Kun Huang. The book was originally started by Born in c. 1940, and was finished in the 1950s by Huang in consultation with Born. The text is considered a classical treatise on the subject of lattice dynamics, phonon theory, and elasticity in crystalline solids, but excluding metals and other complex solids with order/disorder phenomena. J. D. Eshelby, Melvin Lax, and A. J. C. Wilson reviewed the book in 1955, among several others. The book introduces the concept of Cauchy–Born rule and Born–Huang approximation. See also * Bibliography of Max Born * ''Introduction to Solid State Physics ''Introduction to Solid State Physics'', known colloquially as ''Kittel'', is a classic condensed matter physics textbook written by American physicist Charles Kittel in 1953. The book has been highly influential and has seen widespread adoptio ...'' References E ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
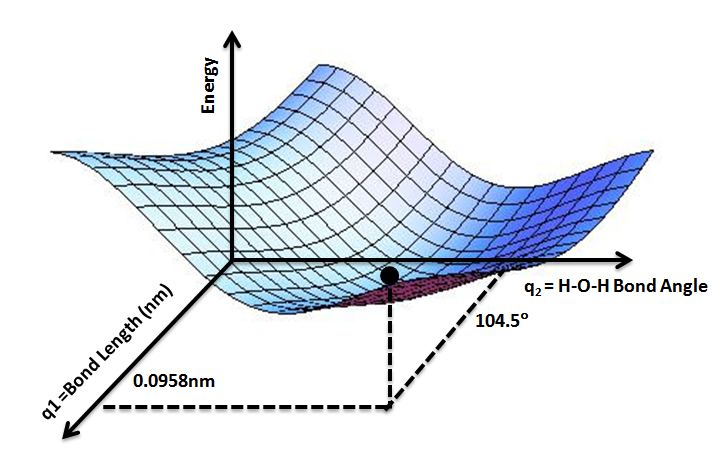
Potential Energy Surface
A potential energy surface (PES) or energy landscape describes the energy of a Physical system, system, especially a collection of atoms, in terms of certain Parameter, parameters, normally the positions of the atoms. The Surface (mathematics), surface might define the energy as a Function (mathematics), function of one or more coordinates; if there is only one coordinate, the surface is called a ''potential energy curve'' or energy profile. An example is the Morse/Long-range potential. It is helpful to use the analogy of a landscape: for a system with two Degrees of freedom (physics and chemistry), degrees of freedom (e.g. two bond lengths), the value of the energy (analogy: the height of the land) is a function of two bond lengths (analogy: the coordinates of the position on the ground). The PES concept finds application in fields such as physics, chemistry and biochemistry, especially in the theoretical sub-branches of these subjects. It can be used to theoretically explore p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vibronic Coupling
Vibronic coupling (also called nonadiabatic coupling or derivative coupling) in a molecule involves the interaction between electronic and nuclear vibrational motion. The term "vibronic" originates from the combination of the terms "vibrational" and "electronic", denoting the idea that in a molecule, vibrational and electronic interactions are interrelated and influence each other. The magnitude of vibronic coupling reflects the degree of such interrelation. In theoretical chemistry, the vibronic coupling is neglected within the Born–Oppenheimer approximation. Vibronic couplings are crucial to the understanding of nonadiabatic processes, especially near points of conical intersections. The direct calculation of vibronic couplings used to be uncommon due to difficulties associated with its evaluation, but has recently gained popularity due to increased interest in the quantitative prediction of internal conversion rates, as well as the development of cheap but rigorous ways ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Born–Oppenheimer Approximation
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense ferment in the development of quantum mechanics. The approximation is widely used in quantum chemistry to speed up the computation of molecular wavefunctions and other properties for large molecules. There are cases where the assumption of separable motion no longer holds, which make the approximation lose validity (it is said to "break down"), but even then the ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Born Rule
The Cauchy–Born rule or Cauchy–Born approximation is a basic hypothesis used in the mathematical formulation of solid mechanics which relates the movement of atoms in a crystal to the overall deformation of the bulk solid. A widespread simplified version states that in a crystalline solid subject to a small strain, the positions of the atoms within the crystal lattice follow the overall strain of the medium. The rule first appears in Max Born and Huang Kun's ''Dynamical Theory of Crystal Lattices'', a refinement of Augustin-Louis Cauchy's relations which were used to derive the equations satisfied by the Cauchy stress tensor. Description To give a more precise definition, consider a crystalline body where the position of the atoms can be described by a set of reference lattice vectors \mathbf^0. The Cauchy–Born rules states that if the body is deformed by a deformation whose gradient is \mathbf, the lattice of the deform body can be described by \mathbf = \mathbf \mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of Molecule, molecules, Material, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed Wave function, wave functions as well as to observable properties such as structures, spectra, and Thermodynamics, thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the Quantization (physics), quantization of energy on a molecular scale can be obtained ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximations
An approximation is anything that is intentionally similar but not exactly equal to something else. Etymology and usage The word ''approximation'' is derived from Latin ''approximatus'', from ''proximus'' meaning ''very near'' and the prefix ''ad-'' (''ad-'' before ''p'' becomes ap- by assimilation) meaning ''to''. Words like ''approximate'', ''approximately'' and ''approximation'' are used especially in technical or scientific contexts. In everyday English, words such as ''roughly'' or ''around'' are used with a similar meaning. It is often found abbreviated as ''approx.'' The term can be applied to various properties (e.g., value, quantity, image, description) that are nearly, but not exactly correct; similar, but not exactly the same (e.g., the approximate time was 10 o'clock). Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws. In science, approximation can refer to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |