|
CLs Upper Limits
In particle physics, CLs represents a statistical method for setting ''upper limits'' (also called ''exclusion limits'') on model parameters, a particular form of interval estimation used for parameters that can take only non-negative values. Although CLs are said to refer to Confidence Levels, "The method's name is ... misleading, as the CLs exclusion region is not a confidence interval." It was first introduced by physicists working at the LEP experiment at CERN and has since been used by many high energy physics experiments. It is a frequentist method in the sense that the properties of the limit are defined by means of error probabilities, however it differs from standard confidence intervals in that the stated confidence level of the interval is not equal to its coverage probability. The reason for this deviation is that standard upper limits based on a most powerful test necessarily produce empty intervals with some fixed probability when the parameter value is zero, and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Particle Physics
Particle physics or high-energy physics is the study of Elementary particle, fundamental particles and fundamental interaction, forces that constitute matter and radiation. The field also studies combinations of elementary particles up to the scale of protons and neutrons, while the study of combinations of protons and neutrons is called nuclear physics. The fundamental particles in the universe are classified in the Standard Model as fermions (matter particles) and bosons (force-carrying particles). There are three Generation (particle physics), generations of fermions, although ordinary matter is made only from the first fermion generation. The first generation consists of Up quark, up and down quarks which form protons and neutrons, and electrons and electron neutrinos. The three fundamental interactions known to be mediated by bosons are electromagnetism, the weak interaction, and the strong interaction. Quark, Quarks cannot exist on their own but form hadrons. Hadrons that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Probability Distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical description of a Randomness, random phenomenon in terms of its sample space and the Probability, probabilities of Event (probability theory), events (subsets of the sample space). For instance, if is used to denote the outcome of a coin toss ("the experiment"), then the probability distribution of would take the value 0.5 (1 in 2 or 1/2) for , and 0.5 for (assuming that fair coin, the coin is fair). More commonly, probability distributions are used to compare the relative occurrence of many different random values. Probability distributions can be defined in different ways and for discrete or for continuous variables. Distributions with special properties or for especially important applications are given specific names. Introduction A prob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Likelihood Function
A likelihood function (often simply called the likelihood) measures how well a statistical model explains observed data by calculating the probability of seeing that data under different parameter values of the model. It is constructed from the joint probability distribution of the random variable that (presumably) generated the observations. When evaluated on the actual data points, it becomes a function solely of the model parameters. In maximum likelihood estimation, the argument that maximizes the likelihood function serves as a point estimate for the unknown parameter, while the Fisher information (often approximated by the likelihood's Hessian matrix at the maximum) gives an indication of the estimate's precision. In contrast, in Bayesian statistics, the estimate of interest is the ''converse'' of the likelihood, the so-called posterior probability of the parameter given the observed data, which is calculated via Bayes' rule. Definition The likelihood function, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of The American Statistical Association
The ''Journal of the American Statistical Association'' is a quarterly peer-reviewed scientific journal published by Taylor & Francis on behalf of the American Statistical Association. It covers work primarily focused on the application of statistics, statistical theory and methods in economic, social, physical, engineering, and health sciences. The journal also includes reviews of books which are relevant to the field. The journal was established in 1888 as the ''Publications of the American Statistical Association''. It was renamed ''Quarterly Publications of the American Statistical Association'' in 1912, obtaining its current title in 1922. Reception According to the ''Journal Citation Reports ''Journal Citation Reports'' (''JCR'') is an annual publication by Clarivate. It has been integrated with the Web of Science and is accessed from the Web of Science Core Collection. It provides information about academic journals in the natur ...'', the journal has a 2023 impac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Likelihood Principle
In statistics, the likelihood principle is the proposition that, given a statistical model, all the evidence in a sample relevant to model parameters is contained in the likelihood function. A likelihood function arises from a probability density function considered as a function of its distributional parameterization argument. For example, consider a model which gives the probability density function \; f_X(x \mid \theta)\; of observable random variable \, X \, as a function of a parameter \,\theta~. Then for a specific value \,x\, of \,X~, the function \,\mathcal(\theta \mid x) = f_X(x \mid \theta)\; is a likelihood function of \,\theta~: it gives a measure of how "likely" any particular value of \,\theta\, is, if we know that \,X\, has the value \,x~. The density function may be a density with respect to counting measure, i.e. a probability mass function. Two likelihood functions are ''equivalent'' if one is a scalar multiple of the other. The likelihood princip ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ancillary Statistic
In statistics, ancillarity is a property of a statistic computed on a sample dataset in relation to a parametric model of the dataset. An ancillary statistic has the same distribution regardless of the value of the parameters and thus provides no information about them. It is opposed to the concept of a complete statistic which contains no ancillary information. It is closely related to the concept of a sufficient statistic which contains all of the information that the dataset provides about the parameters. A ancillary statistic is a specific case of a pivotal quantity that is computed only from the data and not from the parameters. They can be used to construct prediction intervals. They are also used in connection with Basu's theorem to prove independence between statistics. This concept was first introduced by Ronald Fisher in the 1920s, but its formal definition was only provided in 1964 by Debabrata Basu. Examples Suppose ''X''1, ..., ''X''''n'' are independent a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditionality Principle
The conditionality principle is a Fisherian principle of statistical inference that Allan Birnbaum formally defined and studied in an article in the Journal of the American Statistical Association, . Informally, the conditionality principle can be taken as the claim that : ''Experiments which were not actually performed are not relevant to any statistical analysis'' and the implicit admonition that unrealized experiments should be ignored: Not included as part of any calculation or discussion of results. Together with the sufficiency principle, Birnbaum's version of the principle implies the famous likelihood principle. Although the relevance of the proof to data analysis remains controversial among statisticians, many Bayesians and likelihoodists consider the likelihood principle foundational for statistical inference. Historical background Some statisticians in the mid 20th century had proposed that a valid statistical analysis must include all of the possible experiments ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conditional Probability
In probability theory, conditional probability is a measure of the probability of an Event (probability theory), event occurring, given that another event (by assumption, presumption, assertion or evidence) is already known to have occurred. This particular method relies on event A occurring with some sort of relationship with another event B. In this situation, the event A can be analyzed by a conditional probability with respect to B. If the event of interest is and the event is known or assumed to have occurred, "the conditional probability of given ", or "the probability of under the condition ", is usually written as or occasionally . This can also be understood as the fraction of probability B that intersects with A, or the ratio of the probabilities of both events happening to the "given" one happening (how many times A occurs rather than not assuming B has occurred): P(A \mid B) = \frac. For example, the probability that any given person has a cough on any given day ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Distribution
In probability theory and statistics, the Poisson distribution () is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known constant mean rate and independently of the time since the last event. It can also be used for the number of events in other types of intervals than time, and in dimension greater than 1 (e.g., number of events in a given area or volume). The Poisson distribution is named after French mathematician Siméon Denis Poisson. It plays an important role for discrete-stable distributions. Under a Poisson distribution with the expectation of ''λ'' events in a given interval, the probability of ''k'' events in the same interval is: :\frac . For instance, consider a call center which receives an average of ''λ ='' 3 calls per minute at all times of day. If the calls are independent, receiving one does not change the probability of when the next on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tevatron
The Tevatron was a circular particle accelerator (active until 2011) in the United States, at the Fermilab, Fermi National Accelerator Laboratory (called ''Fermilab''), east of Batavia, Illinois, and was the highest energy particle collider until the Large Hadron Collider (LHC) of the CERN, European Organization for Nuclear Research (CERN) was built near Geneva, Switzerland. The Tevatron was a synchrotron that accelerated protons and antiprotons in a circumference ring to energies of up to 1 TeV, hence its name. The Tevatron was completed in 1983 at a cost of $120 million and significant upgrade investments were made during its active years of 1983–2011. The main achievement of the Tevatron was the discovery in 1995 of the top quark—the last Elementary particle#Fundamental fermions, fundamental fermion predicted by the Standard Model of particle physics. On July 2, 2012, scientists of the Collider Detector at Fermilab, CDF and D0 experiment, DØ collider experiment teams a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
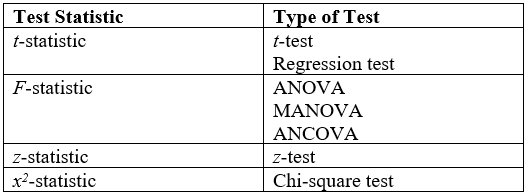
Test Statistic
Test statistic is a quantity derived from the sample for statistical hypothesis testing.Berger, R. L.; Casella, G. (2001). ''Statistical Inference'', Duxbury Press, Second Edition (p.374) A hypothesis test is typically specified in terms of a test statistic, considered as a numerical summary of a data-set that reduces the data to one value that can be used to perform the hypothesis test. In general, a test statistic is selected or defined in such a way as to quantify, within observed data, behaviours that would distinguish the null from the alternative hypothesis, where such an alternative is prescribed, or that would characterize the null hypothesis if there is no explicitly stated alternative hypothesis. An important property of a test statistic is that its sampling distribution under the null hypothesis must be calculable, either exactly or approximately, which allows ''p''-values to be calculated. A ''test statistic'' shares some of the same qualities of a descriptive stat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |