|
1897 In Science
The year 1897 in science and technology involved some significant events, listed below. Chemistry * April 30 – J. J. Thomson first describes his discovery of the electron, in England. Earth sciences * June 12 – 1897 Assam earthquake of magnitude of 8.0 rocks Assam, India, killing over 1,500 people. History of science and technology * Adolf Erik Nordenskiöld publishes ''Periplus: An Essay on the Early History of Charts and Sailing Directions'' in Stockholm. * Boulton and Watt's Smethwick Engine of 1779 in science, 1779 (superseded 1892) is dismantled for preservation by the Birmingham Canal Navigations company, initially at its Ocker Hill depot in the West Midlands of England. Mathematics * David Hilbert unifies the field of algebraic number theory with his treatise ''Zahlbericht''. * John Edward Campbell originates the Baker–Campbell–Hausdorff formula for multiplication of exponentials in Lie algebras. * Raoul Bricard investigates and classifies flexible polyhedra, d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebraic Number Theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic objects such as algebraic number fields and their rings of integers, finite fields, and Algebraic function field, function fields. These properties, such as whether a ring (mathematics), ring admits unique factorization, the behavior of ideal (ring theory), ideals, and the Galois groups of field (mathematics), fields, can resolve questions of primary importance in number theory, like the existence of solutions to Diophantine equations. History Diophantus The beginnings of algebraic number theory can be traced to Diophantine equations, named after the 3rd-century Alexandrian mathematician, Diophantus, who studied them and developed methods for the solution of some kinds of Diophantine equations. A typical Diophantine problem is to find two in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Association
The Mathematical Association is a professional society concerned with mathematics education in the UK. History It was founded in 1871 as the Association for the Improvement of Geometrical Teaching and renamed to the Mathematical Association in 1897. It was the first teachers' subject organisation formed in England. In March 1927, it held a three-day meeting in Grantham to commemorate the bicentenary of the death of Sir Isaac Newton, attended by Sir J. J. Thomson (discoverer of the electron), Sir Frank Watson Dyson – the Astronomer Royal, Sir Horace Lamb, and G. H. Hardy. In 1951, Mary Cartwright became the first female president of the Mathematical Association. In the 1960s, when comprehensive education was being introduced, the Association was in favour of the 11-plus system. For maths teachers training at university, a teaching award that was examined was the Diploma of the Mathematical Association, later known as the Diploma in Mathematical Education of the Mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bar-le-Duc
Bar-le-Duc (), formerly known as Bar, is a commune in the Meuse département, of which it is the capital. The department is in Grand Est in northeastern France. The lower, more modern and busier part of the town extends along a narrow valley, shut in by wooded or vine-clad hills, and is traversed by the Ornain, which is crossed by several bridges. It is bordered on the north-east by the Marne–Rhine Canal and on the south-west by a small arm of the Ornain called the ''Canal des Usines'', on the left bank of which the upper town (''Ville Haute'') is situated. The highly rarefied Bar-le-duc jelly, also known as Lorraine jelly, is a spreadable preparation of white currant or red currant fruit preserves. First mentioned in the historical record in 1344, it is also colloquially referred to as "Bar caviar". History Bar-le-Duc was at one time the seat of the county, from 1354 the Duchy of Bar. Though probably of ancient origin, the town was unimportant until the 10th cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is ��the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which ��will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Henri Brocard
Pierre René Jean Baptiste Henri Brocard (; 12 May 1845 – 16 January 1922) was a French meteorologist and mathematician, in particular a geometer. His best-known achievement is the invention and discovery of the properties of the Brocard points, the Brocard circle, and the Brocard triangle, all bearing his name. Contemporary mathematician Nathan Court wrote that he, along with Émile Lemoine and Joseph Neuberg, was one of the three co-founders of modern triangle geometry. He was awarded the Ordre des Palmes Académiques, and was an officer of the Légion d'honneur. He spent most of his life studying meteorology as an officer in the French Navy, but seems to have made no notable original contributions to the subject. Biography Early years Pierre René Jean Baptiste Henri Brocard was born on 12 May 1845, in Vignot, Meuse to Elizabeth Auguste Liouville and Jean Sebastien Brocard. He attended the Lycée in Marseille as a young child, and then the Lycée in Strasbour ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal De Mathématiques Pures Et Appliquées
The ''Journal de Mathématiques Pures et Appliquées'' () is a French monthly scientific journal of mathematics, founded in 1836 by Joseph Liouville (editor: 1836–1874). The journal was originally published by Charles Louis Étienne Bachelier. After Bachelier's death in 1853, publishing passed to his son-in-law, Louis Alexandre Joseph Mallet, and the journal was marked Mallet-Bachelier. The publisher was sold to Gauthier-Villars ( fr) in 1863, where it remained for many decades. The journal is currently published by Elsevier. According to the 2018 Journal Citation Reports, its impact factor is 2.464. Articles are written in English or French. References External links * Online access* http://sites.mathdoc.fr/JMPA/ Index of freely available volumes Up to 1945, volumes of Journal de Mathématiques Pures et Appliquées are available online free in their entirety from Internet Archive The Internet Archive is an American 501(c)(3) organization, non-profit organiz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
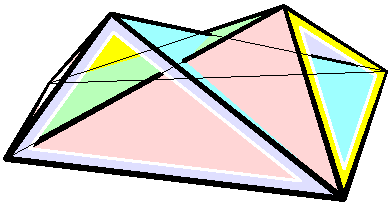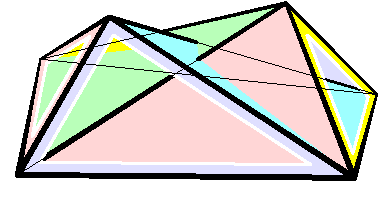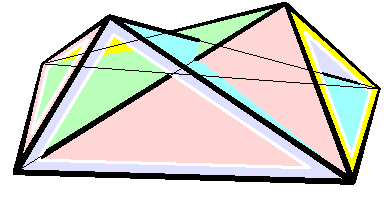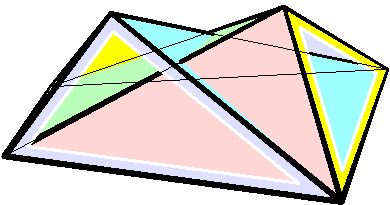
Bricard Octahedron
In geometry Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ..., a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897. The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces. These octahedra were the first flexible polyhedra to be discovered.. The Bricard octahedra have six vertices, twelve edges, and eight triangular faces, connected in the same way as a regular octahedron. Unlike the regular octahedron, the Bricard octahedra are all non-convex self-crossing polyhedra. By Cauchy's rigidity theorem, a flexible polyhedron must be non-convex, but there exist other flexible polyhedra without self-crossings. Avoiding self-crossing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flexible Polyhedra
In geometry, a flexible polyhedron is a polyhedral surface without any boundary edges, whose shape can be continuously changed while keeping the shapes of all of its faces unchanged. The Cauchy rigidity theorem shows that in dimension 3 such a polyhedron cannot be convex (this is also true in higher dimensions). Examples The first examples of flexible polyhedra, now called Bricard octahedra, were discovered by . They are self-intersecting surfaces isometric to an octahedron. The first example of a flexible non-self-intersecting surface in \mathbb^3, the Connelly sphere, was discovered by . Steffen's polyhedron is another non-self-intersecting flexible polyhedron derived from Bricard's octahedra. Bellows conjecture In the late 1970s Connelly and D. Sullivan formulated the bellows conjecture stating that the volume of a flexible polyhedron is invariant under flexing. This conjecture was proved for polyhedra homeomorphic to a sphere by using elimination theory, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Raoul Bricard
Raoul Bricard (23 March 1870 – 26 November 1943) was a French engineer and a mathematician. He is best known for his work in geometry, especially descriptive geometry and scissors congruence, and kinematics, especially mechanical linkages. Biography Bricard taught geometry at Ecole Centrale des Arts et Manufactures. In 1908 he became a professor of applied geometry at the National Conservatory of Arts and Crafts in Paris. In 1932 he received the Poncelet Prize in mathematics from the Paris Academy of Sciences for his work in geometry. Work In 1896 Bricard published a paper on Hilbert's third problem, even before the problem was stated by Hilbert. In it he proved that mirror symmetric polytopes are scissors congruent, and proved a weak version of Dehn's criterion. In 1897 Bricard published an important investigation on flexible polyhedra. In it he classified all flexible octahedra, now known as Bricard octahedra. This work was the subject of Henri Lebesgue's lectu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Proceedings Of The London Mathematical Society
The London Mathematical Society (LMS) is one of the United Kingdom's learned societies for mathematics (the others being the Royal Statistical Society (RSS), the Institute of Mathematics and its Applications (IMA), the Edinburgh Mathematical Society and the Operational Research Society (ORS). History The Society was established on 16 January 1865, the first president being Augustus De Morgan. The earliest meetings were held in University College, but the Society soon moved into Burlington House, Piccadilly. The initial activities of the Society included talks and publication of a journal. The LMS was used as a model for the establishment of the American Mathematical Society in 1888. Mary Cartwright was the first woman to be President of the LMS (in 1961–62). The Society was granted a royal charter in 1965, a century after its foundation. In 1998 the Society moved from rooms in Burlington House into De Morgan House (named after the society's first president), at 57–5 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lie Algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi identity. In other words, a Lie algebra is an algebra over a field for which the multiplication operation (called the Lie bracket) is alternating and satisfies the Jacobi identity. The Lie bracket of two vectors x and y is denoted ,y/math>. A Lie algebra is typically a non-associative algebra. However, every associative algebra gives rise to a Lie algebra, consisting of the same vector space with the commutator Lie bracket, ,y= xy - yx . Lie algebras are closely related to Lie groups, which are groups that are also smooth manifolds: every Lie group gives rise to a Lie algebra, which is the tangent space at the identity. (In this case, the Lie bracket measures the failure of commutativity for the Lie group.) Conversely, to any finite-di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |