|
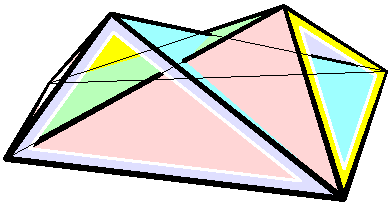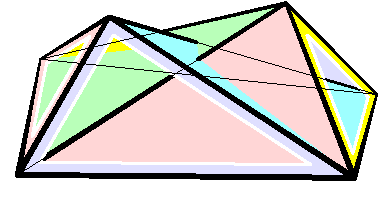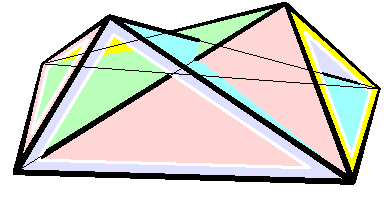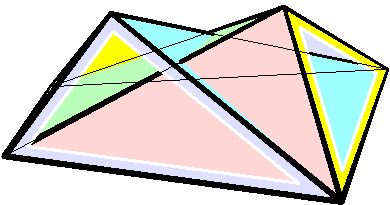
Bricard Octahedron
In geometry Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ..., a Bricard octahedron is a member of a family of flexible polyhedra constructed by Raoul Bricard in 1897. The overall shape of one of these polyhedron may change in a continuous motion, without any changes to the lengths of its edges nor to the shapes of its faces. These octahedra were the first flexible polyhedra to be discovered.. The Bricard octahedra have six vertices, twelve edges, and eight triangular faces, connected in the same way as a regular octahedron. Unlike the regular octahedron, the Bricard octahedra are all non-convex self-crossing polyhedra. By Cauchy's rigidity theorem, a flexible polyhedron must be non-convex, but there exist other flexible polyhedra without self-crossings. Avoiding self-crossing ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces'' of any positive integer dimension ''n'', which are called Euclidean ''n''-spaces when one wants to specify their dimension. For ''n'' equal to one or two, they are commonly called respectively Euclidean lines and Euclidean planes. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called '' postulates'', which either were considered as evid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics Of Rigidity
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonconvex Polyhedra
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting. Each polyhedron can contain either star polygon faces, star polygon vertex figures, or both. The complete set of 57 nonprismatic uniform star polyhedra includes the 4 regular ones, called the Kepler–Poinsot polyhedron, Kepler–Poinsot polyhedra, 14 Quasiregular polyhedron#Nonconvex examples, quasiregular ones, and 39 semiregular ones. There are also two infinite sets of Uniform_polyhedron#.28p_2_2.29_Prismatic_.5Bp.2C2.5D.2C_I2.28p.29_family_.28Dph_dihedral_symmetry.29, ''uniform star prisms'' and ''uniform star antiprisms''. Just as (nondegenerate) star polygons (which have density (polytope), polygon density greater than 1) correspond to circular polygons with overlapping Tessellation, tiles, star polyhedra that do not pass through the center have polytope density greater than 1, and correspond to spherical polyhe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kokotsakis Polyhedron
Kokotsakis polyhedron is a polyhedral surface in three-dimensional space consisting of any number sided of a polygon as its base, and quadrilaterals are its lateral faces with triangles between the consecutive quadrilateral; for n -sided polygonal base of a polyhedron, there are n quadrilaterals and n triangles. Properties and history The polyhedron was discovered when studied the meshes wherein the perimeter of a polygon is surrounded by other polygons, showing an infinitesimally flexible in the case of a quadrilateral base, which was later known as Kokotsakis mesh. More examples of this special case of a Kokotsakis polyhedron were discovered by other mathematicians. Here, a polyhedron is flexible if the shape can be continuously changed while preserving the faces unchanged. Each of its vertexes is said to be "developable", meaning the sum of its plane angle is 2 \pi , resulting in the polyhedral surface being an origami crease pattern, which satisfies the Kawasaki's the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that appeared more than 2000 years ago in Euclid's ''Elements'': "The urvedline is ��the first species of quantity, which has only one dimension, namely length, without any width nor depth, and is nothing else than the flow or run of the point which ��will leave from its imaginary moving some vestige in length, exempt of any width." This definition of a curve has been formalized in modern mathematics as: ''A curve is the image of an interval to a topological space by a continuous function''. In some contexts, the function that defines the curve is called a ''parametrization'', and the curve is a parametric curve. In this article, these curves are sometimes called ''topological curves'' to distinguish them from more constrained curves suc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rigid Origami
Rigid origami is a branch of origami which is concerned with folding structures using flat rigid sheets joined by hinges. That is, unlike in traditional origami, the panels of the paper cannot be bent during the folding process; they must remain flat at all times, and the paper only folded along its hinges. A rigid origami model would still be foldable if it was made from glass sheets with hinges in place of its crease lines. However, there is no requirement that the structure start as a single flat sheet – for instance shopping bags with flat bottoms are studied as part of rigid origami. Rigid origami is a part of the study of the mathematics of paper folding, and rigid origami structures can be considered as a type of mechanical linkage. Rigid origami has great practical utility. Mathematics The number of standard origami bases that can be folded using rigid origami is restricted by its rules. Rigid origami does not have to follow the Huzita–Hatori axioms, the fold l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Horn (anatomy)
A horn is a permanent pointed projection on the head of various animals that consists of a covering of keratin and other proteins surrounding a core of live bone. Horns are distinct from antlers, which are not permanent. In mammals, true horns are found mainly among the ruminant artiodactyls, in the families Antilocapridae ( pronghorn) and Bovidae ( cattle, goats, antelope etc.). Cattle horns arise from subcutaneous connective tissue (under the scalp) and later fuse to the underlying frontal bone. One pair of horns is usual; however, two or more pairs occur in a few wild species and in some domesticated breeds of sheep. Polycerate (multi-horned) sheep breeds include the Hebridean, Icelandic, Jacob, Manx Loaghtan, and the Navajo-Churro. Horns usually have a curved or spiral shape, often with ridges or fluting. In many species, only males have horns. Horns start to grow soon after birth and continue to grow throughout the life of the animal (except in pronghorns, whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentagonal Bipyramid
The pentagonal bipyramid (or pentagonal dipyramid) is a polyhedron with ten triangular faces. It is constructed by attaching two pentagonal pyramids to each of their bases. If the triangular faces are equilateral, the pentagonal bipyramid is an example of deltahedra, composite polyhedron, and Johnson solid. The pentagonal bipyramid may be represented as four-connected well-covered graph. This polyhedron may be used in the chemical compound as the description of an atom cluster known as pentagonal bipyramidal molecular geometry, as a solution in Thomson problem, as well as in decahedral nanoparticles. Special cases As a right bipyramid Like other bipyramids, the pentagonal bipyramid can be constructed by attaching the base of two pentagonal pyramids. These pyramids cover their pentagonal base, such that the resulting polyhedron has ten triangles as its faces, fifteen edges, and seven vertices. The pentagonal bipyramid is said to be right if the pyramids are symmetri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steffen's Polyhedron
In geometry, Steffen's polyhedron is a flexible polyhedron discovered (in 1978) by and named after . It is based on the Bricard octahedron, but unlike the Bricard octahedron its surface does not cross itself.. It has nine vertices, 21 edges, and 14 triangular faces.. Its faces can be decomposed into three subsets: two six-triangle-patches from a Bricard octahedron, and two more triangles (the central two triangles of the net shown in the illustration) that link these patches together.. It obeys the strong bellows conjecture, meaning that (like the Bricard octahedron on which it is based) its Dehn invariant stays constant as it flexes. Although it has been claimed to be the simplest possible flexible polyhedron without self-crossings, a 2024 preprint by Gallet et al. claims to construct a simpler non-self-crossing flexible polyhedron with only eight vertices. References External linksSteffen's Polyhedron Greg Egan Greg Egan (born 20 August 1961) is an Australian science ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dehn Invariant
In geometry, the Dehn invariant is a value used to determine whether one polyhedron can be cut into pieces and reassembled (" dissected") into another, and whether a polyhedron or its dissections can tile space. It is named after Max Dehn, who used it to solve Hilbert's third problem by proving that certain polyhedra with equal volume cannot be dissected into each other. Two polyhedra have a dissection into polyhedral pieces that can be reassembled into either one, if and only if their volumes and Dehn invariants are equal. Having Dehn invariant zero is a necessary (but not sufficient) condition for being a space-filling polyhedron, and a polyhedron can be cut up and reassembled into a space-filling polyhedron if and only if its Dehn invariant is zero. The Dehn invariant of a self-intersection-free flexible polyhedron is invariant as it flexes. Dehn invariants are also an invariant for dissection in higher dimensions, and (with volume) a complete invariant in four dimensions. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Polygon
In geometry, a skew polygon is a closed polygonal chain in Euclidean space. It is a figure (geometry), figure similar to a polygon except its Vertex (geometry), vertices are not all coplanarity, coplanar. While a polygon is ordinarily defined as a plane figure, the edge (geometry), edges and vertices of a skew polygon form a space curve. Skew polygons must have at least four vertices. The ''interior'' surface (geometry), surface and corresponding area measure of such a polygon is not uniquely defined. Skew infinite polygons (apeirogons) have vertices which are not all colinear. A zig-zag skew polygon or antiprismatic polygonRegular complex polytopes, p. 6 has vertices which alternate on two parallel planes, and thus must be even-sided. Regular skew polygons in 3 dimensions (and regular skew apeirogons in two dimensions) are always zig-zag. Skew polygons in three dimensions A regular skew polygon is a faithful symmetric realization of a polygon in dimension greater than 2. In ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |