|
Bussgang Theorem
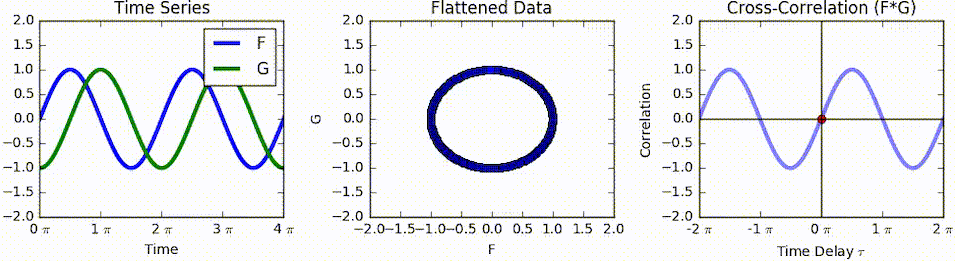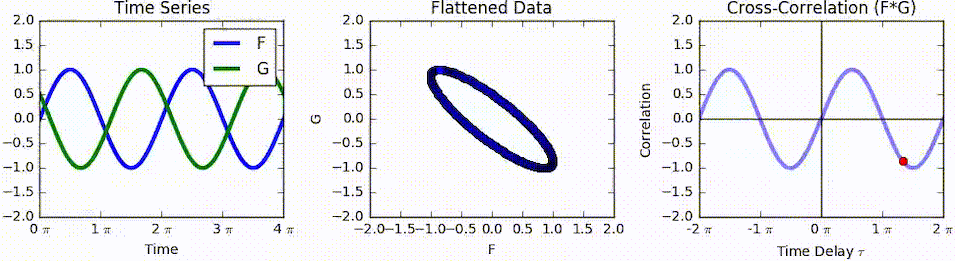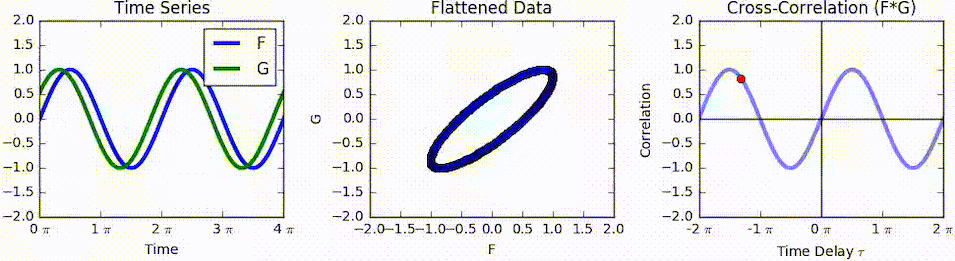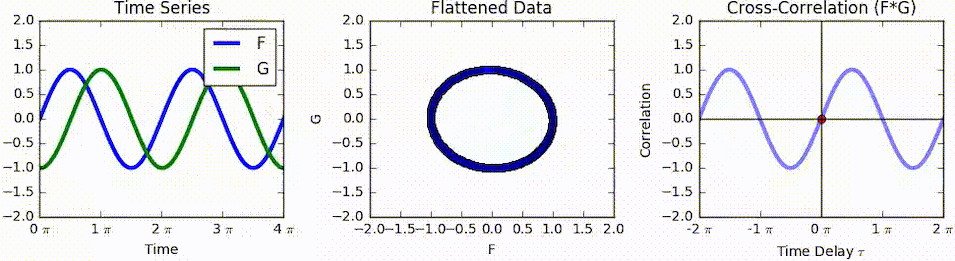
In mathematics, the Bussgang theorem is a theorem of stochastic analysis. The theorem states that the cross-correlation of a Gaussian signal before and after it has passed through a nonlinear operation are equal up to a constant. It was first published by Julian J. Bussgang in 1952 while he was at the Massachusetts Institute of Technology.J.J. Bussgang,"Cross-correlation function of amplitude-distorted Gaussian signals", Res. Lab. Elec., Mas. Inst. Technol., Cambridge MA, Tech. Rep. 216, March 1952. Statement Let \left\ be a zero-mean stationary Gaussian random process and \left \ = g(X(t)) where g(\cdot) is a nonlinear amplitude distortion. If R_X(\tau) is the autocorrelation function of \left\, then the cross-correlation function In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theorem
In mathematics, a theorem is a statement that has been proved, or can be proved. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to establish that the theorem is a logical consequence of the axioms and previously proved theorems. In the mainstream of mathematics, the axioms and the inference rules are commonly left implicit, and, in this case, they are almost always those of Zermelo–Fraenkel set theory with the axiom of choice, or of a less powerful theory, such as Peano arithmetic. A notable exception is Wiles's proof of Fermat's Last Theorem, which involves the Grothendieck universes whose existence requires the addition of a new axiom to the set theory. Generally, an assertion that is explicitly called a theorem is a proved result that is not an immediate consequence of other known theorems. Moreover, many authors qualify as ''theorems'' only the most important results, and use the terms ''lemma'', ''proposition'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stochastic Process
In probability theory and related fields, a stochastic () or random process is a mathematical object usually defined as a family of random variables. Stochastic processes are widely used as mathematical models of systems and phenomena that appear to vary in a random manner. Examples include the growth of a bacterial population, an electrical current fluctuating due to thermal noise, or the movement of a gas molecule. Stochastic processes have applications in many disciplines such as biology, chemistry, ecology, neuroscience, physics, image processing, signal processing, control theory, information theory, computer science, cryptography and telecommunications. Furthermore, seemingly random changes in financial markets have motivated the extensive use of stochastic processes in finance. Applications and the study of phenomena have in turn inspired the proposal of new stochastic processes. Examples of such stochastic processes include the Wiener process or Brownian motion ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross-correlation
In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy. In probability and statistics, the term ''cross-correlations'' refers to the correlations between the entries of two random vectors \mathbf and \mathbf, while the ''correlations'' of a random vector \mathbf are the correlations between the entries of \mathbf itself, those forming the correlation mat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Noise
Gaussian noise, named after Carl Friedrich Gauss, is a term from signal processing theory denoting a kind of signal noise that has a probability density function (pdf) equal to that of the normal distribution (which is also known as the Gaussian distribution). In other words, the values that the noise can take are Gaussian-distributed. The probability density function p of a Gaussian random variable z is given by: : p_G(z) = \frac e^ where z represents the grey level, \mu the mean grey value and \sigma its standard deviation. A special case is ''White Gaussian noise'', in which the values at any pair of times are identically distributed and statistically independent (and hence uncorrelated). In communication channel testing and modelling, Gaussian noise is used as additive white noise to generate additive white Gaussian noise. In telecommunications and computer networking A computer network is a set of computers sharing resources located on or provided by netwo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julian J
Julian may refer to: People * Julian (emperor) (331–363), Roman emperor from 361 to 363 * Julian (Rome), referring to the Roman gens Julia, with imperial dynasty offshoots * Saint Julian (other), several Christian saints * Julian (given name), people with the given name Julian * Julian (surname), people with the surname Julian * Julian (singer), Russian pop singer Places * Julian, California, a census-designated place in San Diego County * Julian, Kansas, an unincorporated community in Stanton County * Julian, Nebraska, a village in Nemaha County * Julian, North Carolina, a census-designated place in Guilford County * Julian, Pennsylvania, an unincorporated community and census-designated place in Centre County * Julian, West Virginia, an unincorporated community in Boone County Other uses * ''Julian'' (album), a 1976 album by Pepper Adams * ''Julian'' (novel), a 1964 novel by Gore Vidal about the emperor * Julian (geology), a substage of the Carnian stage of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Massachusetts Institute Of Technology
The Massachusetts Institute of Technology (MIT) is a Private university, private Land-grant university, land-grant research university in Cambridge, Massachusetts. Established in 1861, MIT has played a key role in the development of modern technology and science, and is one of the most prestigious and highly ranked academic institutions in the world. Founded in response to the increasing Technological and industrial history of the United States, industrialization of the United States, MIT adopted a European History of European universities, polytechnic university model and stressed laboratory instruction in applied science and engineering. MIT is one of three private land grant universities in the United States, the others being Cornell University and Tuskegee University. The institute has an Campus of the Massachusetts Institute of Technology, urban campus that extends more than a mile (1.6 km) alongside the Charles River, and encompasses a number of major off-campus fa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gaussian Process
In probability theory and statistics, a Gaussian process is a stochastic process (a collection of random variables indexed by time or space), such that every finite collection of those random variables has a multivariate normal distribution, i.e. every finite linear combination of them is normally distributed. The distribution of a Gaussian process is the joint distribution of all those (infinitely many) random variables, and as such, it is a distribution over functions with a continuous domain, e.g. time or space. The concept of Gaussian processes is named after Carl Friedrich Gauss because it is based on the notion of the Gaussian distribution (normal distribution). Gaussian processes can be seen as an infinite-dimensional generalization of multivariate normal distributions. Gaussian processes are useful in statistical modelling, benefiting from properties inherited from the normal distribution. For example, if a random process is modelled as a Gaussian process, the distribu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autocorrelation Function
Autocorrelation, sometimes known as serial correlation in the discrete time case, is the correlation of a signal with a delayed copy of itself as a function of delay. Informally, it is the similarity between observations of a random variable as a function of the time lag between them. The analysis of autocorrelation is a mathematical tool for finding repeating patterns, such as the presence of a periodic signal obscured by noise, or identifying the missing fundamental frequency in a signal implied by its harmonic frequencies. It is often used in signal processing for analyzing functions or series of values, such as time domain signals. Different fields of study define autocorrelation differently, and not all of these definitions are equivalent. In some fields, the term is used interchangeably with autocovariance. Unit root processes, trend-stationary processes, autoregressive processes, and moving average processes are specific forms of processes with autocorrelation. Au ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cross-correlation Function
In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy. In probability and statistics, the term ''cross-correlations'' refers to the correlations between the entries of two random vectors \mathbf and \mathbf, while the ''correlations'' of a random vector \mathbf are the correlations between the entries of \mathbf itself, those forming the correlation matrix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.jpg)