cross-correlation function

In signal processing, cross-correlation is a measure of similarity of two series as a function of the displacement of one relative to the other. This is also known as a ''sliding dot product'' or ''sliding inner-product''. It is commonly used for searching a long signal for a shorter, known feature. It has applications in pattern recognition, single particle analysis, electron tomography, averaging, cryptanalysis, and neurophysiology. The cross-correlation is similar in nature to the convolution of two functions. In an autocorrelation, which is the cross-correlation of a signal with itself, there will always be a peak at a lag of zero, and its size will be the signal energy.

In probability and statistics, the term ''cross-correlations'' refers to the correlations between the entries of two random vectors $\mathbf$ and $\mathbf$, while the ''correlations'' of a random vector $\mathbf$ are the correlations between the entries of $\mathbf$ itself, those forming the correlation matrix of $\mathbf$. If each of $\mathbf$ and $\mathbf$ is a scalar random variable which is realized repeatedly in a time series, then the correlations of the various temporal instances of $\mathbf$ are known as ''autocorrelations'' of $\mathbf$, and the cross-correlations of $\mathbf$ with $\mathbf$ across time are temporal cross-correlations. In probability and statistics, the definition of correlation always includes a standardising factor in such a way that correlations have values between −1 and +1.

If $X$ and $Y$ are two independent random variables with probability density functions $f$ and $g$, respectively, then the probability density of the difference $Y - X$ is formally given by the cross-correlation (in the signal-processing sense) $f \star g$; however, this terminology is not used in probability and statistics. In contrast, the convolution $f * g$ (equivalent to the cross-correlation of $f(t)$ and $g(-t)$) gives the probability density function of the sum $X + Y$.

Cross-correlation of deterministic signals

For continuous functions $f$ and $g$, the cross-correlation is defined as:$(f \star g)(\tau)\ \triangleq \int_^ \overline g(t+\tau)\,dt$which is equivalent to$(f \star g)(\tau)\ \triangleq \int_^ \overline g(t)\,dt$where $\overline$ denotes the complex conjugate of $f(t)$, and $\tau$ is called ''displacement'' or ''lag''.

For highly-correlated $f$ and $g$ which have a maximum cross-correlation at a particular $\tau$, a feature in $f$ at $t$ also occurs later in $g$ at $t+\tau$, hence $g$ could be described to ''lag'' $f$ by $\tau$.

If $f$ and $g$ are both continuous periodic functions of period $T$, the integration from $-\infty$ to $\infty$ is replaced by integration over any interval _0,t_0+T/math> of length $T$:$(f \star g)(\tau)\ \triangleq \int_^ \overline g(t + \tau)\,dt$which is equivalent to$(f \star g)(\tau)\ \triangleq \int_^ \overline g(t)\,dt$Similarly, for discrete functions, the cross-correlation is defined as:(f \star g) \triangleq \sum_^ \overline g +n/math>which is equivalent to:(f \star g) \triangleq \sum_^ \overline g /math>For finite discrete functions $f,g\in\mathbb^N$, the (circular) cross-correlation is defined as:(f \star g) \triangleq \sum_^ \overline g m+n)_/math>which is equivalent to:(f \star g) \triangleq \sum_^ \overline g /math>For finite discrete functions $f\in\mathbb^N$, $g\in\mathbb^M$, the kernel cross-correlation is defined as:(f \star g) \triangleq \sum_^ \overline K_g m+n)_/math>where K_g = (g, T_0(g)), k(g, T_1(g)), \dots, k(g, T_(g))/math> is a vector of kernel functions $k(\cdot, \cdot)\colon \mathbb^M \times \mathbb^M \to \mathbb$ and $T_i(\cdot)\colon \mathbb^M \to \mathbb^M$ is an affine transform.

Specifically, $T_i(\cdot)$ can be circular translation transform, rotation transform, or scale transform, etc. The kernel cross-correlation extends cross-correlation from linear space to kernel space. Cross-correlation is equivariant to translation; kernel cross-correlation is equivariant to any affine transforms, including translation, rotation, and scale, etc.

Explanation

As an example, consider two real valued functions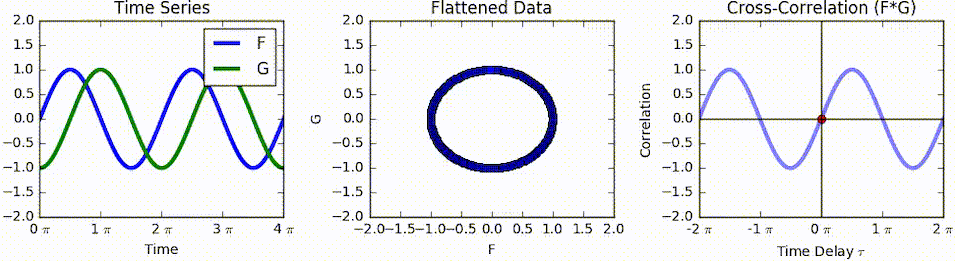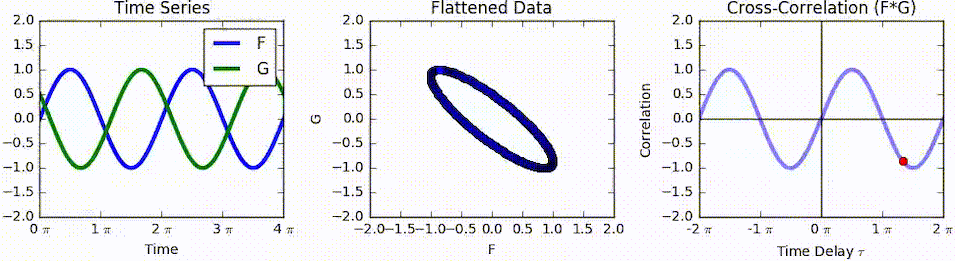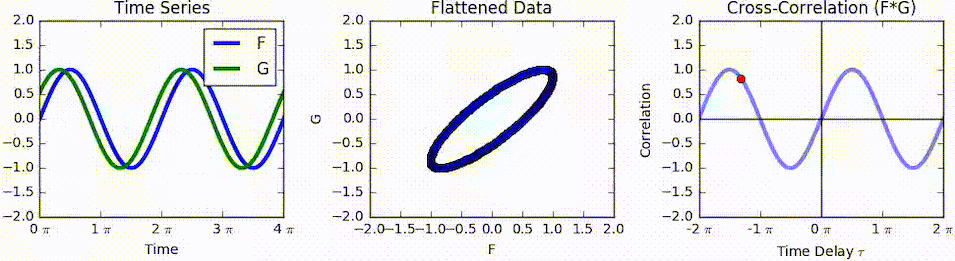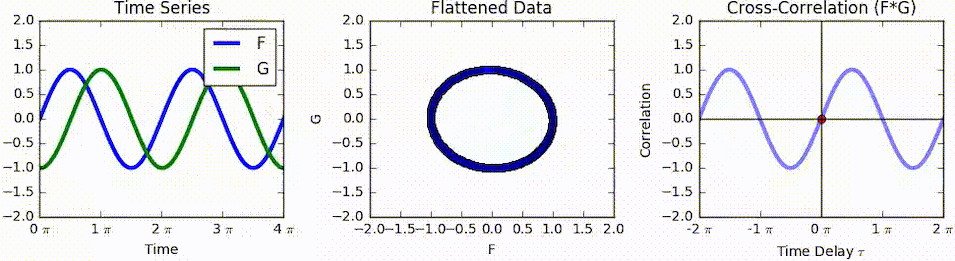 $f$ and $g$ differing only by an unknown shift along the x-axis. One can use the cross-correlation to find how much $g$ must be shifted along the x-axis to make it identical to $f$. The formula essentially slides the $g$ function along the x-axis, calculating the integral of their product at each position. When the functions match, the value of $(f\star g)$ is maximized. This is because when peaks (positive areas) are aligned, they make a large contribution to the integral. Similarly, when troughs (negative areas) align, they also make a positive contribution to the integral because the product of two negative numbers is positive.

With complex-valued functions $f$ and $g$, taking the conjugate of $f$ ensures that aligned peaks (or aligned troughs) with imaginary components will contribute positively to the integral.

In econometrics, lagged cross-correlation is sometimes referred to as cross-autocorrelation.

Properties

Cross-correlation of random vectors

Definition

For random vectors $\mathbf = (X_1,\ldots,X_m)$ and $\mathbf = (Y_1,\ldots,Y_n)$, each containing random elements whose expected value and variance exist, the cross-correlation matrix of $\mathbf$ and $\mathbf$ is defined by\operatorname_ \triangleq\ \operatorname\left mathbf \mathbf\right/math>and has dimensions $m \times n$. Written component-wise:\operatorname_ =
\begin
\operatorname _1 Y_1& \operatorname _1 Y_2& \cdots & \operatorname _1 Y_n\\ \\
\operatorname _2 Y_1& \operatorname _2 Y_2& \cdots & \operatorname _2 Y_n\\ \\
\vdots & \vdots & \ddots & \vdots \\ \\
\operatorname _m Y_1& \operatorname _m Y_2& \cdots & \operatorname _m Y_n\end
The random vectors $\mathbf$ and $\mathbf$ need not have the same dimension, and either might be a scalar value.
Where $\operatorname$ is the expectation value.

Example

For example, if $\mathbf = \left( X_1,X_2,X_3 \right)$ and $\mathbf = \left( Y_1,Y_2 \right)$ are random vectors, then $\operatorname_$ is a $3 \times 2$ matrix whose $(i,j)$-th entry is \operatorname _i Y_j/math>.

Definition for complex random vectors

If $\mathbf = (Z_1,\ldots,Z_m)$ and $\mathbf = (W_1,\ldots,W_n)$ are complex random vectors, each containing random variables whose expected value and variance exist, the cross-correlation matrix of $\mathbf$ and $\mathbf$ is defined by\operatorname_ \triangleq\ \operatorname mathbf \mathbf^/math>where $^$ denotes Hermitian transposition.

Cross-correlation of stochastic processes

In time series analysis and statistics, the cross-correlation of a pair of random process is the correlation between values of the processes at different times, as a function of the two times. Let $(X_t, Y_t)$ be a pair of random processes, and $t$ be any point in time ($t$ may be an integer for a discrete-time process or a real number for a continuous-time process). Then $X_t$ is the value (or realization) produced by a given run of the process at time $t$.

Cross-correlation function

Suppose that the process has means $\mu_X(t)$ and $\mu_Y(t)$ and variances $\sigma_X^2(t)$ and $\sigma_Y^2(t)$ at time $t$, for each $t$. Then the definition of the cross-correlation between times $t_1$ and $t_2$ is\operatorname_(t_1, t_2) \triangleq\ \operatorname\left _ \overline\right/math>where $\operatorname$ is the expected value operator. Note that this expression may be not defined.

Cross-covariance function

Subtracting the mean before multiplication yields the cross-covariance between times $t_1$ and $t_2$:\operatorname_(t_1, t_2) \triangleq\ \operatorname\left left(X_ - \mu_X(t_1)\right)\overline\right/math>Note that this expression is not well-defined for all time series or processes, because the mean or variance may not exist.

Definition for wide-sense stationary stochastic process

Let $(X_t, Y_t)$ represent a pair of stochastic processes that are jointly wide-sense stationary. Then the cross-covariance function and the cross-correlation function are given as follows.

Cross-correlation function

\operatorname_(\tau) \triangleq\ \operatorname\left _t \overline\right/math> or equivalently \operatorname_(\tau) = \operatorname\left _ \overline\right/math>

Cross-covariance function

\operatorname_(\tau) \triangleq\ \operatorname\left left(X_t - \mu_X\right)\overline\right/math> or equivalently \operatorname_(\tau) = \operatorname\left left(X_ - \mu_X\right)\overline\right/math>where $\mu_X$ and $\sigma_X$ are the mean and standard deviation of the process $(X_t)$, which are constant over time due to stationarity; and similarly for $(Y_t)$, respectively. \operatorname /math> indicates the expected value. That the cross-covariance and cross-correlation are independent of $t$ is precisely the additional information (beyond being individually wide-sense stationary) conveyed by the requirement that $(X_t, Y_t)$ are ''jointly'' wide-sense stationary.

The cross-correlation of a pair of jointly wide sense stationary stochastic processes can be estimated by averaging the product of samples measured from one process and samples measured from the other (and its time shifts). The samples included in the average can be an arbitrary subset of all the samples in the signal (e.g., samples within a finite time window or a sub-sampling of one of the signals). For a large number of samples, the average converges to the true cross-correlation.

Normalization

It is common practice in some disciplines (e.g. statistics and time series analysis) to normalize the cross-correlation function to get a time-dependent Pearson correlation coefficient. However, in other disciplines (e.g. engineering) the normalization is usually dropped and the terms "cross-correlation" and "cross-covariance" are used interchangeably.

The definition of the normalized cross-correlation of a stochastic process is$\rho_(t_1, t_2) = \frac = \frac$If the function $\rho_$ is well-defined, its value must lie in the range 1,1/math>, with 1 indicating perfect correlation and −1 indicating perfect anti-correlation.

For jointly wide-sense stationary stochastic processes, the definition is$\rho_(\tau) = \frac = \frac$The normalization is important both because the interpretation of the autocorrelation as a correlation provides a scale-free measure of the strength of statistical dependence, and because the normalization has an effect on the statistical properties of the estimated autocorrelations.

Properties

Symmetry property

For jointly wide-sense stationary stochastic processes, the cross-correlation function has the following symmetry property:Kun Il Park, Fundamentals of Probability and Stochastic Processes with Applications to Communications, Springer, 2018, 978-3-319-68074-3$\operatorname_(t_1, t_2) = \overline$Respectively for jointly WSS processes:$\operatorname_(\tau) = \overline$

Time delay analysis

Cross-correlations are useful for determining the time delay between two signals, e.g., for determining time delays for the propagation of acoustic signals across a microphone array. After calculating the cross-correlation between the two signals, the maximum (or minimum if the signals are negatively correlated) of the cross-correlation function indicates the point in time where the signals are best aligned; i.e., the time delay between the two signals is determined by the argument of the maximum, or arg max of the cross-correlation, as in$\tau_\mathrm=\underset((f \star g)(t))$Terminology in image processing

Zero-normalized cross-correlation (ZNCC)

For image-processing applications in which the brightness of the image and template can vary due to lighting and exposure conditions, the images can be first normalized. This is typically done at every step by subtracting the mean and dividing by the standard deviation. That is, the cross-correlation of a template $t(x,y)$ with a subimage $f(x,y)$ is

$\frac \sum_\left(f(x,y) - \mu_f \right)\left(t(x,y) - \mu_t \right)$

where $n$ is the number of pixels in $t(x,y)$ and $f(x,y)$,
$\mu_f$ is the average of $f$ and $\sigma_f$ is standard deviation of $f$.

In functional analysis terms, this can be thought of as the dot product of two normalized vectors. That is, if$F(x,y) = f(x,y) - \mu_f$and$T(x,y) = t(x,y) - \mu_t$then the above sum is equal to$\left\langle\frac,\frac\right\rangle$where $\langle\cdot,\cdot\rangle$ is the inner product and $\, \cdot\,$ is the ''L''² norm. Cauchy–Schwarz then implies that ZNCC has a range of $$1, 1/math>.

Thus, if $f$ and $t$ are real matrices, their normalized cross-correlation equals the cosine of the angle between the unit vectors $F$ and $T$, being thus $1$ if and only if $F$ equals $T$ multiplied by a positive scalar.

Normalized correlation is one of the methods used for template matching, a process used for finding instances of a pattern or object within an image. It is also the 2-dimensional version of Pearson product-moment correlation coefficient.

Normalized cross-correlation (NCC)

NCC is similar to ZNCC with the only difference of not subtracting the local mean value of intensities:$\frac \sum_f(x,y) t(x,y)$

Nonlinear systems

Caution must be applied when using cross correlation function which assumes Gaussian variance for nonlinear systems. In certain circumstances, which depend on the properties of the input, cross correlation between the input and output of a system with nonlinear dynamics can be completely blind to certain nonlinear effects. This problem arises because some quadratic moments can equal zero and this can incorrectly suggest that there is little "correlation" (in the sense of statistical dependence) between two signals, when in fact the two signals are strongly related by nonlinear dynamics.

See also

* Autocorrelation
* Autocovariance
* Coherence
* Convolution
* Correlation
* Correlation function
* Cross-correlation matrix
* Cross-covariance
* Cross-spectrum
* Digital image correlation
* Phase correlation
* Scaled correlation
* Spectral density
* Wiener–Khinchin theorem

References

Further reading

*

External links

Cross Correlation from Mathworld
* http://scribblethink.org/Work/nvisionInterface/nip.html
* http://www.staff.ncl.ac.uk/oliver.hinton/eee305/Chapter6.pdf

{{Statistics, analysis

Bilinear maps
Covariance and correlation
Signal processing
Time domain analysis