|
Bond Softening
Bond softening is an effect of reducing the strength of a chemical bond by strong laser fields. To make this effect significant, the strength of the electric field in the laser light has to be comparable with the electric field the bonding electron "feels" from the nuclei of the molecule. Such fields are typically in the range of 1–10 V/Å, which corresponds to laser irradiance, intensities 1013–1015 W/cm2. Nowadays, these intensities are routinely achievable from table-top Ti-Sapphire laser, Ti:Sapphire lasers. Theory Theoretical description of bond softening can be traced back to early work on dissociation of diatomic molecules in intense laser fields. While the quantitative description of this process requires quantum mechanics, it can be understood qualitatively using quite simple models. Low-intensity description Consider the simplest diatomic molecule, the dihydrogen cation, H2+ ion. The ground state of this molecule is bonding and the first excited state is antibonding. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Bond
A chemical bond is the association of atoms or ions to form molecules, crystals, and other structures. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds or through the sharing of electrons as in covalent bonds, or some combination of these effects. Chemical bonds are described as having different strengths: there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force, and hydrogen bonding. Since opposite electric charges attract, the negatively charged electrons surrounding the nucleus and the positively charged protons within a nucleus attract each other. Electrons shared between two nuclei will be attracted to both of them. "Constructive quantum mechanical wavefunction interference" stabilizes the paired nuclei (see Theories of chemical bonding). Bonded nuclei maintain an optima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Theorem
The adiabatic theorem is a concept in quantum mechanics. Its original form, due to Max Born and Vladimir Fock (1928), was stated as follows: :''A physical system remains in its instantaneous eigenstate if a given perturbation is acting on it slowly enough and if there is a gap between the eigenvalue and the rest of the Hamiltonian's spectrum.'' In simpler terms, a quantum mechanical system subjected to gradually changing external conditions adapts its functional form, but when subjected to rapidly varying conditions there is insufficient time for the functional form to adapt, so the spatial probability density remains unchanged. Adiabatic pendulum At the 1911 Solvay conference, Einstein gave a lecture on the quantum hypothesis, which states that E = nh \nu for atomic oscillators. After Einstein's lecture, Hendrik Lorentz commented that, classically, if a simple pendulum is shortened by holding the wire between two fingers and sliding down, it seems that its energy will change ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Physics
Molecular physics is the study of the physical properties of molecules and molecular dynamics. The field overlaps significantly with physical chemistry, chemical physics, and quantum chemistry. It is often considered as a sub-field of atomic, molecular, and optical physics. Research groups studying molecular physics are typically designated as one of these other fields. Molecular physics addresses phenomena due to both molecular structure and individual atomic processes within molecules. Like atomic physics, it relies on a combination of classical and quantum mechanics to describe interactions between electromagnetic radiation and matter. Experiments in the field often rely heavily on techniques borrowed from atomic physics, such as spectroscopy and scattering. Molecular structure In a molecule, both the electrons and nuclei experience similar-scale forces from the Coulomb interaction. However, the nuclei remain at nearly fixed locations in the molecule while the electrons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conical Intersection
In quantum chemistry, a conical intersection of two or more potential energy surfaces is the set of molecular geometry points where the potential energy surfaces are degenerate (intersect) and the non-adiabatic couplings between these states are non-vanishing. In the vicinity of conical intersections, the Born–Oppenheimer approximation breaks down and the coupling between electronic and nuclear motion becomes important, allowing non-adiabatic processes to take place. The location and characterization of conical intersections are therefore essential to the understanding of a wide range of important phenomena governed by non-adiabatic events, such as photoisomerization, photosynthesis, vision and the photostability of DNA. Conical intersections are also called molecular funnels or diabolic points as they have become an established paradigm for understanding reaction mechanisms in photochemistry as important as transitions states in thermal chemistry. This comes from the very impo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-of-flight Mass Spectrometry
Time-of-flight mass spectrometry (TOFMS) is a method of mass spectrometry in which an ion's mass-to-charge ratio is determined by a time of flight measurement. Ions are accelerated by an electric field of known strength. This acceleration results in an ion having the same kinetic energy as any other ion that has the same charge. The velocity of the ion depends on the mass-to-charge ratio (heavier ions of the same charge reach lower speeds, although ions with higher charge will also increase in velocity). The time that it subsequently takes for the ion to reach a detector at a known distance is measured. This time will depend on the velocity of the ion, and therefore is a measure of its mass-to-charge ratio. From this ratio and known experimental parameters, one can identify the ion. Theory The potential energy of a charged particle in an electric field is related to the charge of the particle and to the strength of the electric field: where ''E''p is potential energy, ''q'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
YAG Laser
YAG, YaG, Yağ, or yag can refer to: * Yttrium aluminium garnet, a synthetic crystal used in solid-state laser systems * Fort Frances Municipal Airport, Ontario, Canada, IATA code * YMCA Youth and Government, a model government program for youth * Yahgan language, spoken in Chile and Argentina, ISO 639 code * Cansu Yağ (born 1990), a female Turkish footballer * YAG training vessels, wooden Canadian Navy boats 1954–1955 * List of yard and district craft of the United States Navy#District auxiliary, miscellaneous (YAG), District auxiliary, miscellaneous (YAG), US Navy hull classification symbol {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Philip H
Philip, also Phillip, is a male name derived from the Greek (''Philippos'', lit. "horse-loving" or "fond of horses"), from a compound of (''philos'', "dear", "loved", "loving") and (''hippos'', "horse"). Prominent Philips who popularized the name include kings of Macedonia and one of the apostles of early Christianity. ''Philip'' has many alternative spellings. One derivation often used as a surname is Phillips. The original Greek spelling includes two Ps as seen in Philippides and Philippos, which is possible due to the Greek endings following the two Ps. To end a word with such a double consonant—in Greek or in English—would, however, be incorrect. It has many diminutive (or even hypocoristic) forms including Phil, Philly, Phillie, Lip, and Pip. There are also feminine forms such as Philippine and Philippa. Philip in other languages * Afrikaans: Filip * Albanian: Filip * Amharic: ፊሊጶስ (Filip'os) * Arabic: فيلبس (Fīlibus), فيليبوس (Fīl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Landau–Zener Formula
The Landau–Zener formula is an analytic solution to the equations of motion governing the transition dynamics of a two-state quantum system, with a time-dependent Hamiltonian varying such that the energy separation of the two states is a linear function of time. The formula, giving the probability of a diabatic (not adiabatic) transition between the two energy states, was published separately by Lev Landau, Clarence Zener, Ernst Stueckelberg, and Ettore Majorana, in 1932. If the system starts, in the infinite past, in the lower energy eigenstate, we wish to calculate the probability of finding the system in the upper energy eigenstate in the infinite future (a so-called Landau–Zener transition). For infinitely slow variation of the energy difference (that is, a Landau–Zener velocity of zero), the adiabatic theorem tells us that no such transition will take place, as the system will always be in an instantaneous eigenstate of the Hamiltonian at that moment in time. At non- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
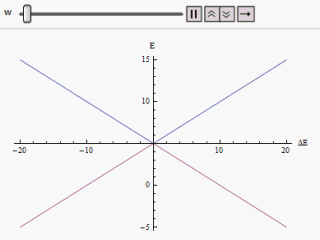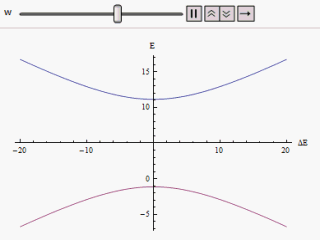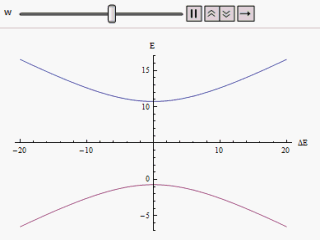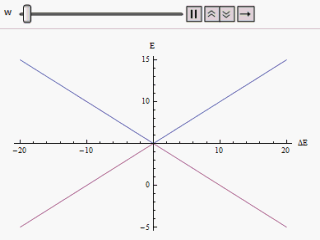
Avoided Crossing
In quantum physics and quantum chemistry, an avoided crossing (AC, sometimes called intended crossing, non-crossing or anticrossing) is the phenomenon where two eigenvalues of a Hermitian matrix representing a quantum observable and depending on k continuous real parameters cannot become equal in value ("cross") except on a manifold of dimension k-2 . The phenomenon is also known as the von Neumann–Wigner theorem. In the case of a diatomic molecule (with one parameter, namely the bond length), this means that the eigenvalues cannot cross at all. In the case of a triatomic molecule, this means that the eigenvalues can coincide only at a single point (see conical intersection). This is particularly important in quantum chemistry. In the Born–Oppenheimer approximation, the electronic molecular Hamiltonian is diagonalized on a set of distinct molecular geometries (the obtained eigenvalues are the values of the adiabatic potential energy surfaces). The geometries for which ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irradiance
In radiometry, irradiance is the radiant flux ''received'' by a ''surface'' per unit area. The SI unit of irradiance is the watt per square metre (symbol W⋅m−2 or W/m2). The CGS unit erg per square centimetre per second (erg⋅cm−2⋅s−1) is often used in astronomy. Irradiance is often called intensity, but this term is avoided in radiometry where such usage leads to confusion with radiant intensity. In astrophysics, irradiance is called ''radiant flux''. Spectral irradiance is the irradiance of a surface per unit frequency or wavelength, depending on whether the spectrum is taken as a function of frequency or of wavelength. The two forms have different dimensions and units: spectral irradiance of a frequency spectrum is measured in watts per square metre per hertz (W⋅m−2⋅Hz−1), while spectral irradiance of a wavelength spectrum is measured in watts per square metre per metre (W⋅m−3), or more commonly watts per square metre per nanometre (W⋅m−2⋅nm−1) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix Diagonalisation
In linear algebra, a square matrix A is called diagonalizable or non-defective if it is similar to a diagonal matrix. That is, if there exists an invertible matrix P and a diagonal matrix D such that . This is equivalent to (Such D are not unique.) This property exists for any linear map: for a finite-dimensional vector space a linear map T:V\to V is called diagonalizable if there exists an ordered basis of V consisting of eigenvectors of T. These definitions are equivalent: if T has a matrix representation A = PDP^ as above, then the column vectors of P form a basis consisting of eigenvectors of and the diagonal entries of D are the corresponding eigenvalues of with respect to this eigenvector basis, T is represented by Diagonalization is the process of finding the above P and and makes many subsequent computations easier. One can raise a diagonal matrix D to a power by simply raising the diagonal entries to that power. The determinant of a diagonal matrix is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Hamiltonian
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity. The elementary parts of a molecule are the nuclei, characterized by their atomic numbers, ''Z'', and the electrons, which have negative elementary charge, −''e''. Their interaction gives a nuclear charge of ''Z'' + ''q'', where , with ''N'' equal to the number of electrons. Electrons and nuclei are, to a very good approximation, point charges and point masses. The molecular Hamiltonian is a sum of several terms: its major terms are the kinetic energies of the electrons and the C ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |