Avoided crossing on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 However, when subjected to an external perturbation, the matrix elements of the Hamiltonian change. For the sake of simplicity we consider a perturbation with only off diagonal elements. Since the overall Hamiltonian must be Hermitian we may simply write the new Hamiltonian
:
Where P is the perturbation with zero diagonal terms. The fact that P is Hermitian fixes its off-diagonal components. The modified eigenstates can be found by diagonalising the modified Hamiltonian. It turns out that the new eigenvalues and are
:
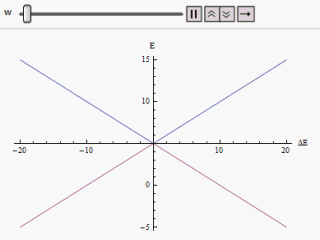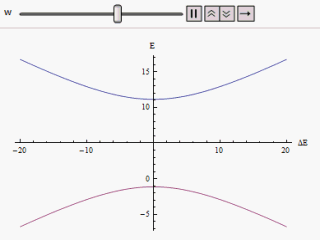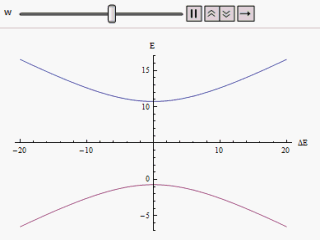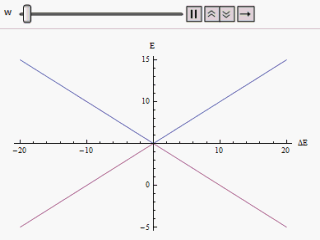
If a graph is plotted varying along the horizontal axis and or along the vertical, we find two branches of a hyperbola (as shown in the figure). The curve asymptotically approaches the original unperturbed energy levels. Analyzing the curves it becomes evident that even if the original states were degenerate (i.e. ) the new energy states are no longer equal. However, if is set to zero we may find at , and the levels cross. Thus with the effect of the perturbation these level crossings are avoided.
However, when subjected to an external perturbation, the matrix elements of the Hamiltonian change. For the sake of simplicity we consider a perturbation with only off diagonal elements. Since the overall Hamiltonian must be Hermitian we may simply write the new Hamiltonian
:
Where P is the perturbation with zero diagonal terms. The fact that P is Hermitian fixes its off-diagonal components. The modified eigenstates can be found by diagonalising the modified Hamiltonian. It turns out that the new eigenvalues and are
:
If a graph is plotted varying along the horizontal axis and or along the vertical, we find two branches of a hyperbola (as shown in the figure). The curve asymptotically approaches the original unperturbed energy levels. Analyzing the curves it becomes evident that even if the original states were degenerate (i.e. ) the new energy states are no longer equal. However, if is set to zero we may find at , and the levels cross. Thus with the effect of the perturbation these level crossings are avoided.
 However it turns out that the two-state Hamiltonian of benzene is not diagonal. The off-diagonal elements result into lowering of energy and the benzene molecule stabilizes in a structure which is a superposition of these symmetric ones with energy
However it turns out that the two-state Hamiltonian of benzene is not diagonal. The off-diagonal elements result into lowering of energy and the benzene molecule stabilizes in a structure which is a superposition of these symmetric ones with energy
quantum physics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
and quantum chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions ...
, an avoided crossing (AC, sometimes called intended crossing, non-crossing or anticrossing) is the phenomenon where two eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s of a Hermitian matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the -th row and -th column is equal to the complex conjugate of the element in the ...
representing a quantum observable
In physics, an observable is a physical property or physical quantity that can be measured. In classical mechanics, an observable is a real-valued "function" on the set of all possible system states, e.g., position and momentum. In quantum ...
and depending on continuous real parameters cannot become equal in value ("cross") except on a manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
of dimension . The phenomenon is also known as the von Neumann–Wigner theorem. In the case of a diatomic molecule
Diatomic molecules () are molecules composed of only two atoms, of the same or different chemical elements. If a diatomic molecule consists of two atoms of the same element, such as hydrogen () or oxygen (), then it is said to be homonuclear mol ...
(with one parameter, namely the bond length
In molecular geometry, bond length or bond distance is defined as the average distance between Atomic nucleus, nuclei of two chemical bond, bonded atoms in a molecule. It is a Transferability (chemistry), transferable property of a bond between at ...
), this means that the eigenvalues cannot cross at all. In the case of a triatomic molecule, this means that the eigenvalues can coincide only at a single point (see conical intersection).
This is particularly important in quantum chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions ...
. In the Born–Oppenheimer approximation, the electronic molecular Hamiltonian is diagonalized on a set of distinct molecular geometries (the obtained eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
s are the values of the adiabatic potential energy surfaces). The geometries for which the potential energy surfaces are avoiding to cross are the locus where the Born–Oppenheimer approximation fails.
Avoided crossing also occur in the resonance frequencies of undamped mechanical systems, where the stiffness and mass matrices are real symmetric. There the resonance frequencies are the square root of the generalized eigenvalues.
In two-state systems
Emergence
Study of atwo-level system
In quantum mechanics, a two-state system (also known as a two-level system) is a quantum system that can exist in any quantum superposition of two independent (physically distinguishable) quantum states. The Hilbert space describing such a syste ...
is of vital importance in quantum mechanics because it embodies simplification of many of physically realizable systems. The effect of perturbation on a two-state system Hamiltonian
Hamiltonian may refer to:
* Hamiltonian mechanics, a function that represents the total energy of a system
* Hamiltonian (quantum mechanics), an operator corresponding to the total energy of that system
** Dyall Hamiltonian, a modified Hamiltonian ...
is manifested through avoided crossings in the plot of individual energy versus energy difference curve of the eigenstates. The two-state Hamiltonian can be written as
:
The eigenvalues of which are and and the eigenvector
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by ...
s, and . These two eigenvectors designate the two states of the system. If the system is prepared in either of the states it would remain in that state. If happens to be equal to there will be a twofold degeneracy in the Hamiltonian. In that case any superposition of the degenerate eigenstates is evidently another eigenstate of the Hamiltonian. Hence the system prepared in any state will remain in that forever.
 However, when subjected to an external perturbation, the matrix elements of the Hamiltonian change. For the sake of simplicity we consider a perturbation with only off diagonal elements. Since the overall Hamiltonian must be Hermitian we may simply write the new Hamiltonian
:
Where P is the perturbation with zero diagonal terms. The fact that P is Hermitian fixes its off-diagonal components. The modified eigenstates can be found by diagonalising the modified Hamiltonian. It turns out that the new eigenvalues and are
:
If a graph is plotted varying along the horizontal axis and or along the vertical, we find two branches of a hyperbola (as shown in the figure). The curve asymptotically approaches the original unperturbed energy levels. Analyzing the curves it becomes evident that even if the original states were degenerate (i.e. ) the new energy states are no longer equal. However, if is set to zero we may find at , and the levels cross. Thus with the effect of the perturbation these level crossings are avoided.
However, when subjected to an external perturbation, the matrix elements of the Hamiltonian change. For the sake of simplicity we consider a perturbation with only off diagonal elements. Since the overall Hamiltonian must be Hermitian we may simply write the new Hamiltonian
:
Where P is the perturbation with zero diagonal terms. The fact that P is Hermitian fixes its off-diagonal components. The modified eigenstates can be found by diagonalising the modified Hamiltonian. It turns out that the new eigenvalues and are
:
If a graph is plotted varying along the horizontal axis and or along the vertical, we find two branches of a hyperbola (as shown in the figure). The curve asymptotically approaches the original unperturbed energy levels. Analyzing the curves it becomes evident that even if the original states were degenerate (i.e. ) the new energy states are no longer equal. However, if is set to zero we may find at , and the levels cross. Thus with the effect of the perturbation these level crossings are avoided.
Quantum resonance
The immediate impact of avoided level crossing in a degenerate two state system is the emergence of a lowered energy eigenstate. The effective lowering of energy always correspond to increasing stability.(see: Energy minimization) Bond resonance in organic molecules exemplifies the occurrence of such avoided crossings. To describe these cases we may note that the non-diagonal elements in an erstwhile diagonalised Hamiltonian not only modify the energy eigenvalues but also superpose the old eigenstates into the new ones. These effects are more prominent if the original Hamiltonian had degeneracy. This superposition of eigenstates to attain more stability is precisely the phenomena of chemical bond resonance. Our earlier treatment started by denoting the eigenvectors and as the matrix representation of eigenstates and of a two-state system. Using bra–ket notation the matrix elements of are actually the terms : with where due to the degeneracy of the unperturbed Hamiltonian and the off-diagonal perturbations are and . The new eigenstates and can be found by solving the eigenvalue equations and . From simple calculations it can be shown that : and : where It is evident that both of the new eigenstates are superposition of the original degenerate eigenstates and one of the eigenvalues (here ) is less than the original unperturbed eigenenergy. So the corresponding stable system will naturally mix up the former unperturbed eigenstates to minimize its energy. In the example ofbenzene
Benzene is an Organic compound, organic chemical compound with the Chemical formula#Molecular formula, molecular formula C6H6. The benzene molecule is composed of six carbon atoms joined in a planar hexagonal Ring (chemistry), ring with one hyd ...
the experimental evidences of probable bond structures give rise to two different eigenstates, and . The symmetry of these two structures mandates that .