|
Potential Energy Surface
A potential energy surface (PES) or energy landscape describes the energy of a Physical system, system, especially a collection of atoms, in terms of certain Parameter, parameters, normally the positions of the atoms. The Surface (mathematics), surface might define the energy as a Function (mathematics), function of one or more coordinates; if there is only one coordinate, the surface is called a ''potential energy curve'' or energy profile. An example is the Morse/Long-range potential. It is helpful to use the analogy of a landscape: for a system with two Degrees of freedom (physics and chemistry), degrees of freedom (e.g. two bond lengths), the value of the energy (analogy: the height of the land) is a function of two bond lengths (analogy: the coordinates of the position on the ground). The PES concept finds application in fields such as physics, chemistry and biochemistry, especially in the theoretical sub-branches of these subjects. It can be used to theoretically explore p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
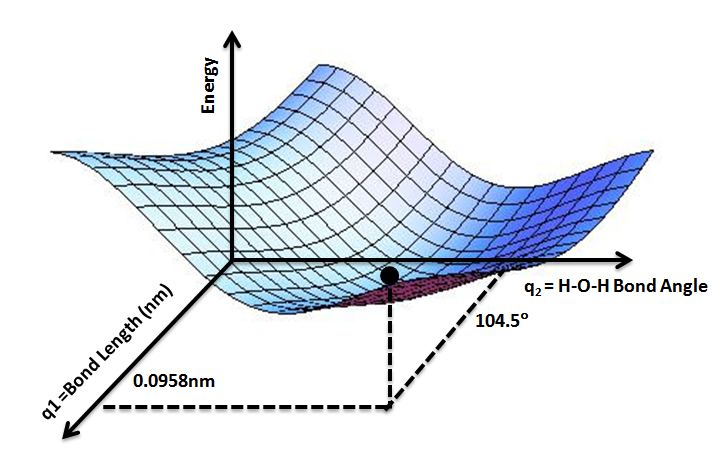
Potential Energy Surface For Water
Potential generally refers to a currently unrealized ability. The term is used in a wide variety of fields, from physics to the social sciences to indicate things that are in a state where they are able to change in ways ranging from the simple release of energy by objects to the realization of abilities in people. The philosopher Aristotle incorporated this concept into his theory of potentiality and actuality (in Greek, ''dynamis'' and ''energeia''), translated into Latin as ''potentia'' and ''actualitas'' (earlier also ''possibilitas'' and ''efficacia''). a pair of closely connected principles which he used to analyze motion, causality, ethics, and physiology in his ''Physics'', ''Metaphysics'', ''Nicomachean Ethics'', and ''De Anima'', which is about the human psyche. That which is potential can theoretically be made actual by taking the right action; for example, a boulder on the edge of a cliff has potential to fall that could be actualized by pushing it over the edge. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Of A Function
In mathematics, the graph of a function f is the set of ordered pairs (x, y), where f(x) = y. In the common case where x and f(x) are real numbers, these pairs are Cartesian coordinates of points in a plane (geometry), plane and often form a Plane curve, curve. The graphical representation of the graph of a Function (mathematics), function is also known as a ''Plot (graphics), plot''. In the case of Bivariate function, functions of two variables – that is, functions whose Domain of a function, domain consists of pairs (x, y) –, the graph usually refers to the set of ordered triples (x, y, z) where f(x,y) = z. This is a subset of three-dimensional space; for a continuous real-valued function of two real variables, its graph forms a Surface (mathematics), surface, which can be visualized as a ''surface plot (graphics), surface plot''. In science, engineering, technology, finance, and other areas, graphs are tools used for many purposes. In the simplest case one variable is p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Geometry
Molecular geometry is the three-dimensional arrangement of the atoms that constitute a molecule. It includes the general shape of the molecule as well as bond lengths, bond angles, torsional angles and any other geometrical parameters that determine the position of each atom. Molecular geometry influences several properties of a substance including its reactivity, polarity, phase of matter, color, magnetism and biological activity. The angles between bonds that an atom forms depend only weakly on the rest of a molecule, i.e. they can be understood as approximately local and hence transferable properties. Determination The molecular geometry can be determined by various spectroscopic methods and diffraction methods. IR, microwave and Raman spectroscopy can give information about the molecule geometry from the details of the vibrational and rotational absorbance detected by these techniques. X-ray crystallography, neutron diffraction and electron diffraction can g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverse Distance Weighting
Inverse distance weighting (IDW) is a type of Deterministic algorithm, deterministic method for multivariate interpolation with a known homogeneously scattered set of points. The assigned values to unknown points are calculated with a Weighted mean, weighted average of the values available at the known points. This method can also be used to create spatial weights matrices in spatial autocorrelation analyses (e.g. Moran's I, Moran's ''I''). The name given to this type of method was motivated by the Weighted mean, weighted average applied, since it resorts to the inverse of the distance to each known point ("amount of proximity") when assigning weights. Definition of the problem The expected result is a discrete assignment of the unknown function u in a study region: :u(x): x \to \mathbb, \quad x \in \mathbf \sub \mathbb^n, where \mathbf is the study region. The set of N known data points can be described as a list of tuples: :[(x_1, u_1), (x_2, u_2), ..., (x_N, u_N)]. The f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Keith J
Keith may refer to: People and fictional characters * Keith (given name), includes a list of people and fictional characters * Keith (surname) * Keith (singer), American singer James Keefer (born 1949) * Keith (gamer), American professional League of Legends player * Baron Keith, a line of Scottish barons in the late 18th century * Clan Keith, a Scottish clan associated with lands in northeastern and northwestern Scotland Places Australia * Keith, South Australia, a town and locality Scotland * Keith, Moray, a town ** Keith railway station * Keith Marischal, East Lothian United States * Keith, Georgia, an unincorporated community * Keith, Ohio, an unincorporated community * Keith, West Virginia, an unincorporated community * Keith, Wisconsin, a ghost town * Keith County, Nebraska Other uses * Keith F.C., a football team based in Keith, Scotland * , a ship of the British Royal Navy * Hurricane Keith, a 2000 hurricane that caused extensive damage in Central America * '' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michael Polanyi
Michael Polanyi ( ; ; 11 March 1891 – 22 February 1976) was a Hungarian-British polymath, who made important theoretical contributions to physical chemistry, economics, and philosophy. He argued that positivism is a false account of knowledge, knowing. His wide-ranging research in Outline of physical science, physical science included chemical kinetics, x-ray diffraction, and adsorption of gases. He pioneered the theory of Fiber diffraction, fibre diffraction analysis in 1921, and the dislocation theory of plastic deformation of Ductility, ductile metals and other materials in 1934. He emigrated to Germany, in 1926 becoming a chemistry professor at the Kaiser Wilhelm Institute in Berlin, and then in 1933 to England, becoming first a chemistry professor, and then a social sciences professor at the Victoria University of Manchester, University of Manchester. Two of his pupils won the Nobel Prize, as well as one of his children. In 1944 Polanyi was elected to the Royal Society ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Henry Eyring (chemist)
Henry Eyring (February 20, 1901 – December 26, 1981) was a Mexico-born United States theoretical chemist whose primary contribution was in the study of chemical reaction rates and intermediates. Eyring developed the Absolute Rate Theory or Transition state theory of chemical reactions, connecting the fields of chemistry and physics through atomic theory, quantum theory, and statistical mechanics. History Eyring, a third-generation member of the Church of Jesus Christ of Latter-day Saints (LDS Church), was reared on a cattle ranch in Colonia Juárez, Chihuahua, a Mormon colony, for the first 11 years of his life. His father, Edward Christian Eyring, practiced plural marriage; Edward married Caroline Romney (1893) and her sister Emma Romney (1903), both daughters of Miles Park Romney, the great-grandfather of Mitt Romney. In July 1912, the Eyrings and about 4,200 other immigrants were driven out of Mexico by violent insurgents during the Mexican Revolution and moved to El P ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fritz London
Fritz Wolfgang London (March 7, 1900 – March 30, 1954) was a German born physicist and professor at Duke University. His fundamental contributions to the theories of chemical bonding and of intermolecular forces (London dispersion forces) are today considered classic and are discussed in standard textbooks of physical chemistry. With his brother Heinz London, he made a significant contribution to understanding electromagnetic properties of superconductors with the London equations and was nominated for the Nobel Prize in Chemistry on five separate occasions. Biography London was born in Breslau, German Empire, Germany (now Wrocław, Poland) as the son of Franz London (1863-1917). Being a Jew, London lost his position at the Humboldt University of Berlin, University of Berlin after Hitler's Nazi Party passed the Law for the Restoration of the Professional Civil Service, 1933 racial laws. He took visiting positions in England and France, and emigrated to the United States in 1939, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Chemistry
Computational chemistry is a branch of chemistry that uses computer simulations to assist in solving chemical problems. It uses methods of theoretical chemistry incorporated into computer programs to calculate the structures and properties of molecules, groups of molecules, and solids. The importance of this subject stems from the fact that, with the exception of some relatively recent findings related to the hydrogen molecular ion (dihydrogen cation), achieving an accurate quantum mechanical depiction of chemical systems analytically, or in a closed form, is not feasible. The complexity inherent in the many-body problem exacerbates the challenge of providing detailed descriptions of quantum mechanical systems. While computational results normally complement information obtained by chemical experiments, it can occasionally predict unobserved chemical phenomena. Overview Computational chemistry differs from theoretical chemistry, which involves a mathematical description of chem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular oriented lines, called '' coordinate lines'', ''coordinate axes'' or just ''axes'' (plural of ''axis'') of the system. The point where the axes meet is called the '' origin'' and has as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame. Similarly, the position of any point in three-dimensional space can be specified by three ''Cartesian coordinates'', which are the signed distances from the point to three mutually perpendicular planes. More generally, Cartesian coordinates specify the point in an -dimensional Euclidean space for any dimension . These coordinates are the signed distances from the point to mutually perpendicular fixed h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter Space
The parameter space is the space of all possible parameter values that define a particular mathematical model. It is also sometimes called weight space, and is often a subset of finite-dimensional Euclidean space. In statistics, parameter spaces are particularly useful for describing parametric families of probability distributions. They also form the background for parameter estimation. In the case of extremum estimators for parametric models, a certain objective function is maximized or minimized over the parameter space. Theorems of existence and consistency of such estimators require some assumptions about the topology of the parameter space. For instance, compactness of the parameter space, together with continuity of the objective function, suffices for the existence of an extremum estimator. Sometimes, parameters are analyzed to view how they affect their statistical model. In that context, they can be viewed as inputs of a function, in which case the technical term for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
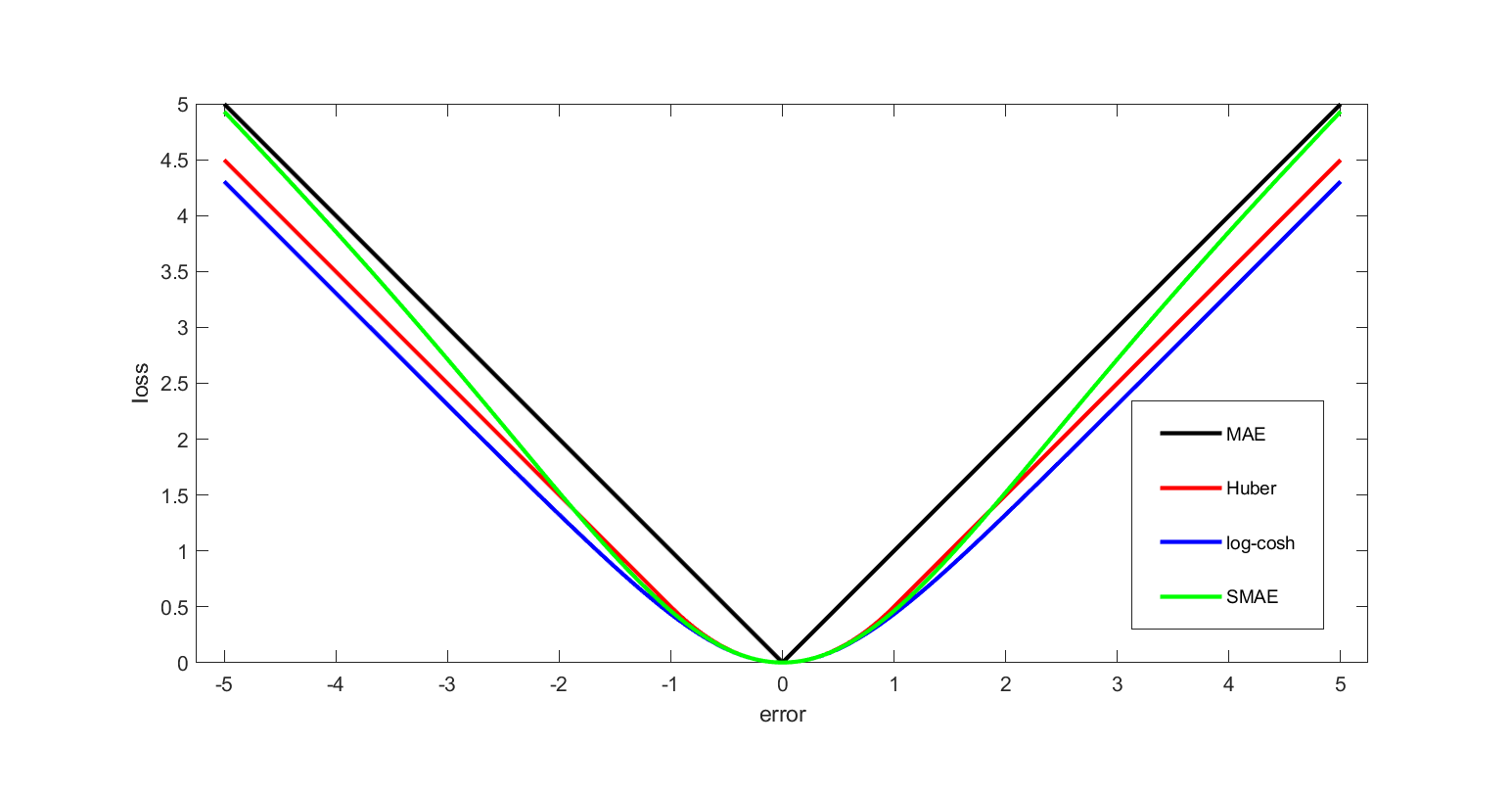
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |