|
Beta Prime Distribution
In probability theory and statistics, the beta prime distribution (also known as inverted beta distribution or beta distribution of the second kindJohnson et al (1995), p 248) is an absolutely continuous probability distribution. If p\in ,1/math> has a beta distribution, then the odds \frac has a beta prime distribution. Definitions Beta prime distribution is defined for x > 0 with two parameters ''α'' and ''β'', having the probability density function: : f(x) = \frac where ''B'' is the Beta function. The cumulative distribution function is : F(x; \alpha,\beta)=I_\left(\alpha, \beta \right) , where ''I'' is the regularized incomplete beta function. While the related beta distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed as a probability, the beta prime distribution is the conjugate prior distribution of the parameter of a Bernoulli distribution expressed in odds. The distribution is a Pearson type VI distribution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beta Prime Pdf
Beta (, ; uppercase , lowercase , or cursive Greek, cursive ; or ) is the second letter of the Greek alphabet. In the system of Greek numerals, it has a value of 2. In Ancient Greek, beta represented the voiced bilabial plosive . In Modern Greek, it represents the voiced bilabial fricative while in borrowed words is instead commonly transcribed as μπ. Letters that arose from beta include the Roman letter and the Cyrillic letters and . Name Like the names of most other Greek letters, the name of beta was adopted from the acrophony, acrophonic name of the corresponding letter in Phoenician alphabet, Phoenician, which was the common Semitic languages, Semitic word ('house', compare and ). In Greek, the name was , pronounced in Ancient Greek. It is spelled in modern monotonic orthography and pronounced . History The letter beta was derived from the Phoenician alphabet, Phoenician letter Bet (letter), beth . The letter Β had the largest number of highly divergent lo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypergeometric Function
In mathematics, the Gaussian or ordinary hypergeometric function 2''F''1(''a'',''b'';''c'';''z'') is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation. For systematic lists of some of the many thousands of published identities involving the hypergeometric function, see the reference works by and . There is no known system for organizing all of the identities; indeed, there is no known algorithm that can generate all identities; a number of different algorithms are known that generate different series of identities. The theory of the algorithmic discovery of identities remains an active research topic. History The term "hypergeometric series" was first used by John Wallis in his 1655 book ''Arithmetica Infinitor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sigmoid-beta Distribution
The term generalized logistic distribution is used as the name for several different families of probability distributions. For example, Johnson et al.Johnson, N.L., Kotz, S., Balakrishnan, N. (1995) ''Continuous Univariate Distributions, Volume 2'', Wiley. (pages 140–142) list four forms, which are listed below. Type I has also been called the skew-logistic distribution. Type IV subsumes the other types and is obtained when applying the logit transform to beta random variates. Following the same convention as for the log-normal distribution, type IV may be referred to as the logistic-beta distribution, with reference to the standard logistic function, which is the inverse of the logit transform. For other families of distributions that have also been called generalized logistic distributions, see the shifted log-logistic distribution, which is a generalization of the log-logistic distribution; and the metalog ("meta-logistic") distribution, which is highly shape-and-bounds f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inverted Dirichlet Distribution
In statistics, the inverted Dirichlet distribution is a multivariate generalization of the beta prime distribution, and is related to the Dirichlet distribution. It was first described by Tiao and Cuttman in 1965. The distribution has a density function given by : p\left(x_1,\ldots, x_k\right) = \frac x_1^\cdots x_k^\times\left(1+\sum_^k x_i\right)^,\qquad x_i>0. The distribution has applications in statistical regression and arises naturally when considering the multivariate Student distribution. It can be characterized by its mixed moments: : E\left prod_^kx_i^\right= \frac\prod_^k\frac provided that q_j>-\nu_j, 1\leqslant j\leqslant k and \nu_>q_1+\ldots+q_k. The inverted Dirichlet distribution is conjugate to the negative multinomial distribution if a generalized form of odds ratio is used instead of the categories' probabilities- if the negative multinomial parameter vector is given by p, by changing parameters of the negative multinomial to x_i = \frac, i = 1\ldots ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lomax Distribution
The Lomax distribution, conditionally also called the Pareto Type II distribution, is a heavy-tail probability distribution used in business, economics, actuarial science, queueing theory and Internet traffic modeling. It is named after K. S. Lomax. It is essentially a Pareto distribution that has been shifted so that its support begins at zero. Characterization Probability density function The probability density function (pdf) for the Lomax distribution is given by :p(x) = \frac\alpha\lambda \left(1 + \frac x\lambda \right)^, \qquad x \geq 0, with shape parameter \alpha > 0 and scale parameter \lambda > 0. The density can be rewritten in such a way that more clearly shows the relation to the Pareto Type I distribution. That is: :p(x) = \frac. Non-central moments The \nuth non-central moment E\left ^\nu\right/math> exists only if the shape parameter \alpha strictly exceeds \nu, when the moment has the value :E\left(X^\nu\right) = \frac. Related distribut ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pareto Distribution
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto, is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actuarial science, actuarial, and many other types of observable phenomena; the principle originally applied to describing the distribution of wealth in a society, fitting the trend that a large portion of wealth is held by a small fraction of the population. The ''Pareto principle'' or "80:20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value () precisely reflect it. Empirical observation has shown that this 80:20 distribution fits a wide range of cases, including natural phenomena and human activities. Definitions If ''X'' is a random variable with a Pareto (Type I) distribution, then the probability that ''X'' is greater than some nu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Log Logistic Distribution
In probability and statistics, the log-logistic distribution (known as the Fisk distribution in economics) is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events whose rate increases initially and decreases later, as, for example, mortality rate from cancer following diagnosis or treatment. It has also been used in hydrology to model stream flow and precipitation, in economics as a simple model of the distribution of wealth or income distribution, income, and in Computer network, networking to model the transmission times of data considering both the network and the software. The log-logistic distribution is the probability distribution of a random variable whose logarithm has a logistic distribution. It is similar in shape to the log-normal distribution but has Heavy-tailed distribution, heavier tails. Unlike the log-normal, its cumulative distribution function can be written in closed form expr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singh–Maddala Distribution
In probability theory, statistics and econometrics, the Burr Type XII distribution or simply the Burr distribution is a continuous probability distribution for a non-negative random variable. It is also known as the Singh–Maddala distribution and is one of a number of different distributions sometimes called the "generalized log-logistic distribution". Definitions Probability density function The Burr (Type XII) distribution has probability density function: : \begin f(x;c,k) & = ck\frac \\ ptf(x;c,k,\lambda) & = \frac \left( \frac \right)^ \left + \left(\frac\right)^c\right \end The \lambda parameter scales the underlying variate and is a positive real. Cumulative distribution function The cumulative distribution function is: :F(x;c,k) = 1-\left(1+x^c\right)^ :F(x;c,k,\lambda) = 1 - \left + \left(\frac\right)^c \right Applications It is most commonly used to model household income, see for example: Household income in the U.S. and compare to magenta graph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dagum Distribution
The Dagum distribution (or Mielke Beta-Kappa distribution) is a continuous probability distribution defined over positive real numbers. It is named after Camilo Dagum, who proposed it in a series of papers in the 1970s. The Dagum distribution arose from several variants of a new model on the size distribution of personal income and is mostly associated with the study of income distribution. There is both a three-parameter specification (Type I) and a four-parameter specification (Type II) of the Dagum distribution; a summary of the genesis of this distribution can be found in "A Guide to the Dagum Distributions". A general source on statistical size distributions often cited in work using the Dagum distribution is ''Statistical Size Distributions in Economics and Actuarial Sciences''. Definition The cumulative distribution function of the Dagum distribution (Type I) is given by :F(x;a,b,p)= \left( 1+\left(\frac\right)^ \right)^ \text x > 0 \text a, b, p > 0 . The corresponding ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-distribution
In probability theory and statistics, the ''F''-distribution or ''F''-ratio, also known as Snedecor's ''F'' distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor), is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other ''F''-tests. Definitions The ''F''-distribution with ''d''1 and ''d''2 degrees of freedom is the distribution of X = \frac where U_1 and U_2 are independent random variables with chi-square distributions with respective degrees of freedom d_1 and d_2. It can be shown to follow that the probability density function (pdf) for ''X'' is given by \begin f(x; d_1,d_2) &= \frac \\ pt&=\frac \left(\frac\right)^ x^ \left(1+\frac \, x \right)^ \end for real ''x'' > 0. Here \mathrm is the beta function. In many applications, the parameters ''d''1 and ''d''2 are positive integers, but the distribution is wel ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
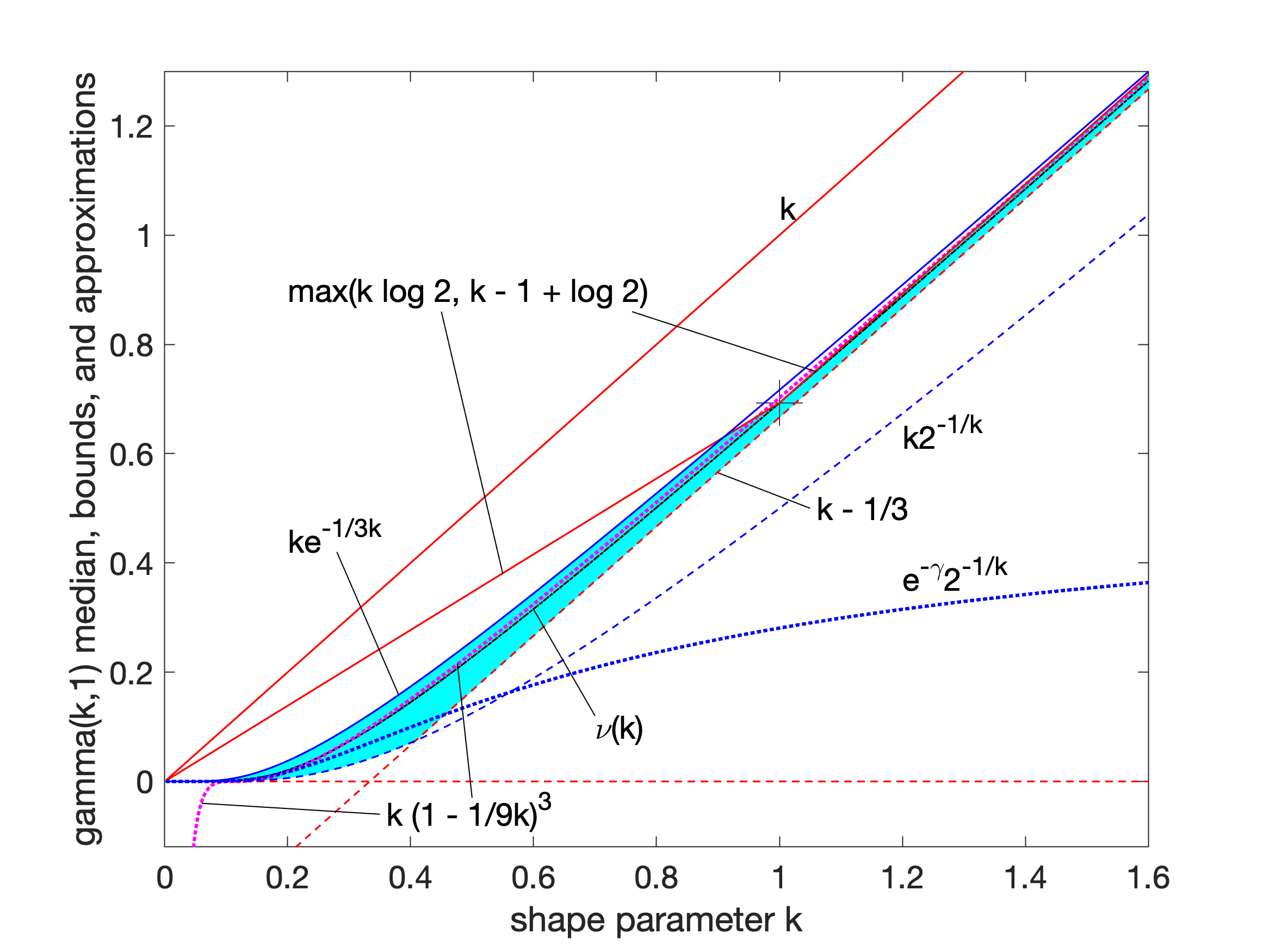
Gamma Distribution
In probability theory and statistics, the gamma distribution is a versatile two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use: # With a shape parameter and a scale parameter # With a shape parameter \alpha and a rate parameter In each of these forms, both parameters are positive real numbers. The distribution has important applications in various fields, including econometrics, Bayesian statistics, and life testing. In econometrics, the (''α'', ''θ'') parameterization is common for modeling waiting times, such as the time until death, where it often takes the form of an Erlang distribution for integer ''α'' values. Bayesian statisticians prefer the (''α'',''λ'') parameterization, utilizing the gamma distribution as a conjugate prior for several inverse scale parameters, facilit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |