|
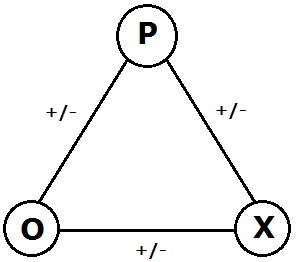
Balance Theory
In the psychology of motivation, balance theory is a theory of attitude change, proposed by Fritz Heider. It conceptualizes the cognitive consistency motive as a drive toward psychological balance. The consistency motive is the urge to maintain one's values and beliefs over time. Heider proposed that "sentiment" or liking relationships are balanced if the affect (psychology), affect valence (psychology), valence in a system multiplies out to a positive result. Research in 2020 provided neuroscientific evidence supporting Heider's balance theory. A study using neuroimaging techniques found distinct differences in brain activation when individuals were exposed to unbalanced versus balanced triads. These differences were observed in brain regions associated with processing cognitive dissonance, offering biological support for Heider's original psychological explanation of balance theory in social context. Structural balance theory in social network analysis is the extension proposed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Psychology
Psychology is the scientific study of mind and behavior. Its subject matter includes the behavior of humans and nonhumans, both consciousness, conscious and Unconscious mind, unconscious phenomena, and mental processes such as thoughts, feelings, and motivation, motives. Psychology is an academic discipline of immense scope, crossing the boundaries between the Natural science, natural and social sciences. Biological psychologists seek an understanding of the Emergence, emergent properties of brains, linking the discipline to neuroscience. As social scientists, psychologists aim to understand the behavior of individuals and groups.Hockenbury & Hockenbury. Psychology. Worth Publishers, 2010. A professional practitioner or researcher involved in the discipline is called a psychologist. Some psychologists can also be classified as Behavioural sciences, behavioral or Cognitive science, cognitive scientists. Some psychologists attempt to understand the role of mental functions in i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Triadic Relation
In mathematics, a ternary relation or triadic relation is a finitary relation in which the number of places in the relation is three. Ternary relations may also be referred to as 3-adic, 3-ary, 3-dimensional, or 3-place. Just as a binary relation is formally defined as a set of ''pairs'', i.e. a subset of the Cartesian product of some sets ''A'' and ''B'', so a ternary relation is a set of triples, forming a subset of the Cartesian product of three sets ''A'', ''B'' and ''C''. An example of a ternary relation in elementary geometry can be given on triples of points, where a triple is in the relation if the three points are collinear. Another geometric example can be obtained by considering triples consisting of two points and a line, where a triple is in the ternary relation if the two points determine (are incident with) the line. Examples Binary functions A function in two variables, mapping two values from sets ''A'' and ''B'', respectively, to a value in ''C'' ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Component (graph Theory)
In graph theory, a component of an undirected graph is a connected subgraph that is not part of any larger connected subgraph. The components of any graph partition its vertices into disjoint sets, and are the induced subgraphs of those sets. A graph that is itself connected has exactly one component, consisting of the whole graph. Components are sometimes called connected components. The number of components in a given graph is an important graph invariant, and is closely related to invariants of matroids, topological spaces, and matrices. In random graphs, a frequently occurring phenomenon is the incidence of a giant component, one component that is significantly larger than the others; and of a percolation threshold, an edge probability above which a giant component exists and below which it does not. The components of a graph can be constructed in linear time, and a special case of the problem, connected-component labeling, is a basic technique in image analysis. Dynamic c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Human Relations
In social psychology, an interpersonal relation (or interpersonal relationship) describes a social association, connection, or affiliation between two or more people. It overlaps significantly with the concept of social relations, which are the fundamental unit of analysis within the social sciences. Relations vary in degrees of intimacy, self-disclosure, duration, reciprocity, and power distribution. The main themes or trends of the interpersonal relations are: family, kinship, friendship, love, marriage, business, employment, clubs, neighborhoods, ethical values, support and solidarity. Interpersonal relations may be regulated by law, custom, or mutual agreement, and form the basis of social groups and societies. They appear when people communicate or act with each other within specific social contexts, and they thrive on equitable and reciprocal compromises. Interdisciplinary analysis of relationships draws heavily upon the other social sciences, including, but no ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
James A
James may refer to: People * James (given name) * James (surname) * James (musician), aka Faruq Mahfuz Anam James, (born 1964), Bollywood musician * James, brother of Jesus * King James (other), various kings named James * Prince James (other) * Saint James (other) Places Canada * James Bay, a large body of water * James, Ontario United Kingdom * James College, York, James College, a college of the University of York United States * James, Georgia, an unincorporated community * James, Iowa, an unincorporated community * James City, North Carolina * James City County, Virginia ** James City (Virginia Company) ** James City Shire * James City, Pennsylvania * St. James City, Florida Film and television * James (2005 film), ''James'' (2005 film), a Bollywood film * James (2008 film), ''James'' (2008 film), an Irish short film * James (2022 film), ''James'' (2022 film), an Indian Kannada-language film * "James", a television Adventure Time (season 5)#ep42, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Project Euclid
Project Euclid is a collaborative partnership between Cornell University Library and Duke University Press which seeks to advance scholarly communication in theoretical and applied mathematics and statistics through partnerships with independent and society publishers. It was created to provide a platform for small publishers of scholarly journals to move from print to electronic in a cost-effective way. Through a combination of support by subscribing libraries and participating publishers, Project Euclid has made 70% of its journal articles available as open access. As of 2010, Project Euclid provided access to over one million pages of open-access content. Mission and goals Project Euclid's stated mission is to advance scholarly communication in the field of theoretical and applied mathematics and statistics. Through a "mixture of open access, subscription, and hosted subscription content it provides a way for small publishers (especially societies) to host their math or statist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Michigan Mathematical Journal
The ''Michigan Mathematical Journal'' (established 1952) is published by the mathematics department at the University of Michigan. An important early editor for the Journal was George Piranian. Historically, the Journal has been published a small number of times in a given year (currently four), in all areas of mathematics Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar .... The current Managing Editor is Mircea Mustaţă. References External links * Mathematics journals University of Michigan 1952 establishments in Michigan Academic journals established in 1952 {{math-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycle (graph Theory)
In graph theory, a cycle in a graph is a non-empty trail in which only the first and last vertices are equal. A directed cycle in a directed graph is a non-empty directed trail in which only the first and last vertices are equal. A graph without cycles is called an ''acyclic graph''. A directed graph without directed cycles is called a '' directed acyclic graph''. A connected graph without cycles is called a ''tree''. Definitions Circuit and cycle * A circuit is a non-empty trail in which the first and last vertices are equal (''closed trail''). : Let be a graph. A circuit is a non-empty trail with a vertex sequence . * A cycle or simple circuit is a circuit in which only the first and last vertices are equal. * ''n'' is called the length of the circuit resp. length of the cycle. Directed circuit and directed cycle * A directed circuit is a non-empty directed trail in which the first and last vertices are equal (''closed directed trail''). : Let be a directed grap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph (discrete Mathematics)
In discrete mathematics, particularly in graph theory, a graph is a structure consisting of a Set (mathematics), set of objects where some pairs of the objects are in some sense "related". The objects are represented by abstractions called ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') and each of the related pairs of vertices is called an ''edge'' (also called ''link'' or ''line''). Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. The edges may be directed or undirected. For example, if the vertices represent people at a party, and there is an edge between two people if they shake hands, then this graph is undirected because any person ''A'' can shake hands with a person ''B'' only if ''B'' also shakes hands with ''A''. In contrast, if an edge from a person ''A'' to a person ''B'' means that ''A'' owes money to ''B'', then this graph is directed, because owing mon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path (graph Theory)
In graph theory, a path in a graph is a finite or infinite sequence of edges which joins a sequence of vertices which, by most definitions, are all distinct (and since the vertices are distinct, so are the edges). A directed path (sometimes called dipath) in a directed graph is a finite or infinite sequence of edges which joins a sequence of distinct vertices, but with the added restriction that the edges be all directed in the same direction. Paths are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts. See e.g. , , or . cover more advanced algorithmic topics concerning paths in graphs. Definitions Walk, trail, and path * A walk is a finite or infinite sequence of edges which joins a sequence of vertices. : Let be a graph. A finite walk is a sequence of edges for which there is a sequence of vertices such that ''Φ''(''e''''i'') = for . is the ''vertex sequence'' of the walk. The walk is ''closed'' if ''v''1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signed Graph
In the area of graph theory in mathematics, a signed graph is a graph in which each edge has a positive or negative sign. A signed graph is balanced if the product of edge signs around every cycle is positive. The name "signed graph" and the notion of balance appeared first in a mathematical paper of Frank Harary in 1953. Dénes Kőnig had already studied equivalent notions in 1936 under a different terminology but without recognizing the relevance of the sign group. At the Center for Group Dynamics at the University of Michigan, Dorwin Cartwright and Harary generalized Fritz Heider's psychological theory of balance in triangles of sentiments to a psychological theory of balance in signed graphs. Signed graphs have been rediscovered many times because they come up naturally in many unrelated areas. For instance, they enable one to describe and analyze the geometry of subsets of the classical root systems. They appear in topological graph theory and group theory. They are ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Enemy Of My Enemy Is My Friend
"The enemy of my enemy is my friend" is an ancient proverb which suggests that two parties can or should work together against a common enemy. The exact meaning of the modern phrase was first expressed in the Latin phrase "Amicus meus, inimicus inimici mei" ("my friend, the enemy of my enemy"), which had become common throughout Europe by the early 18th century, while the first recorded use of the current English version came in 1884. Examples Rajamandala A Sanskrit treatise on statecraft, the ''Arthashastra'' of Kautilya states: A neighboring power would be the first to dispute control of territory, and therefore Kautilya finds neighboring kings to be natural enemies of any conqueror. A king whose territories border those of the enemy would also have this relationship with them, and therefore be a natural ally. This system of relationships was termed Rajamandala (meaning ''circle of kings'') and informed the foreign policy of Chandragupta's Empire. This early theory of geopo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |