|
Adding
Addition (usually signified by the plus symbol ) is one of the four basic operations of arithmetic, the other three being subtraction, multiplication and division. The addition of two whole numbers results in the total amount or ''sum'' of those values combined. The example in the adjacent image shows a combination of three apples and two apples, making a total of five apples. This observation is equivalent to the mathematical expression (that is, "3 ''plus'' 2 is equal to 5"). Besides counting items, addition can also be defined and executed without referring to concrete objects, using abstractions called numbers instead, such as integers, real numbers and complex numbers. Addition belongs to arithmetic, a branch of mathematics. In algebra, another area of mathematics, addition can also be performed on abstract objects such as vectors, matrices, subspaces and subgroups. Addition has several important properties. It is commutative, meaning that the order of the operands d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers—addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today. History The prehistory of arithmetic is limited to a small number of artifacts, which may indicate the conception of addition and subtraction, the best-known being the Ishango bone from central Africa, dating from somewhere between 20,000 and 18,000 BC, although its interpretation is disputed. The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations: addition, subtraction, multiplication, and division, as early as 2000 BC. These artifacts do not always reveal the specific process used for solving problems, b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiplication
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division. The result of a multiplication operation is called a '' product''. The multiplication of whole numbers may be thought of as repeated addition; that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, the ''multiplicand'', as the quantity of the other one, the ''multiplier''. Both numbers can be referred to as ''factors''. :a\times b = \underbrace_ For example, 4 multiplied by 3, often written as 3 \times 4 and spoken as "3 times 4", can be calculated by adding 3 copies of 4 together: :3 \times 4 = 4 + 4 + 4 = 12 Here, 3 (the ''multiplier'') and 4 (the ''multiplicand'') are the ''factors'', and 12 is the ''product''. One of the main properties of multiplica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form a + bi, where and are real numbers. Because no real number satisfies the above equation, was called an imaginary number by René Descartes. For the complex number a+bi, is called the , and is called the . The set of complex numbers is denoted by either of the symbols \mathbb C or . Despite the historical nomenclature "imaginary", complex numbers are regarded in the mathematical sciences as just as "real" as the real numbers and are fundamental in many aspects of the scientific description of the natural world. Complex numbers allow solutions to all polynomial equations, even those that have no solutions in real numbers. More precisely, the fundamental theorem of algebra asserts that every non-constant polynomial equation with re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
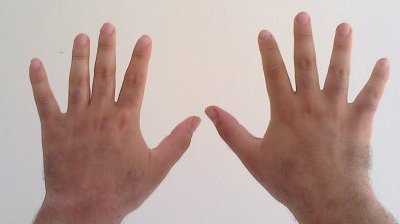
Subtraction
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, . For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken away, resulting in a total of 3 peaches. Therefore, the ''difference'' of 5 and 2 is 3; that is, . While primarily associated with natural numbers in arithmetic, subtraction can also represent removing or decreasing physical and abstract quantities using different kinds of objects including negative numbers, fractions, irrational numbers, vectors, decimals, functions, and matrices. Subtraction follows several important patterns. It is anticommutative, meaning that changing the order changes the sign of the answer. It is also not associative, meaning that when one subtracts more than two numbers, the order in which subtraction is performed matters. Because is the additive identity, subtraction of it does not change a number. Subtracti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers can be represented by symbols, called ''numerals''; for example, "5" is a numeral that represents the number five. As only a relatively small number of symbols can be memorized, basic numerals are commonly organized in a numeral system, which is an organized way to represent any number. The most common numeral system is the Hindu–Arabic numeral system, which allows for the representation of any number using a combination of ten fundamental numeric symbols, called digits. In addition to their use in counting and measuring, numerals are often used for labels (as with telephone numbers), for ordering (as with serial number A serial number is a unique identifier assigned incrementally or sequentially to an item, to ''uniquely'' identi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as ''decimal notation''. A ''decimal numeral'' (also often just ''decimal'' or, less correctly, ''decimal number''), refers generally to the notation of a number in the decimal numeral system. Decimals may sometimes be identified by a decimal separator (usually "." or "," as in or ). ''Decimal'' may also refer specifically to the digits after the decimal separator, such as in " is the approximation of to ''two decimals''". Zero-digits after a decimal separator serve the purpose of signifying the precision of a value. The numbers that may be represented in the decimal system are the decimal fractions. That is, fractions of the form , where is an inte ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrix (mathematics)
In mathematics, a matrix (plural matrices) is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object. For example, \begin1 & 9 & -13 \\20 & 5 & -6 \end is a matrix with two rows and three columns. This is often referred to as a "two by three matrix", a "-matrix", or a matrix of dimension . Without further specifications, matrices represent linear maps, and allow explicit computations in linear algebra. Therefore, the study of matrices is a large part of linear algebra, and most properties and operations of abstract linear algebra can be expressed in terms of matrices. For example, matrix multiplication represents composition of linear maps. Not all matrices are related to linear algebra. This is, in particular, the case in graph theory, of incidence matrices, and adjacency matrices. ''This article focuses on matrices related to linear algebra, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting poin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plus And Minus Signs
The plus and minus signs, and , are mathematical symbols used to represent the notions of positive and negative, respectively. In addition, represents the operation of addition, which results in a sum, while represents subtraction, resulting in a difference. Their use has been extended to many other meanings, more or less analogous. ''Plus'' and ''minus'' are Latin terms meaning "more" and "less", respectively. History Though the signs now seem as familiar as the alphabet or the Hindu-Arabic numerals, they are not of great antiquity. The Egyptian hieroglyphic sign for addition, for example, resembled a pair of legs walking in the direction in which the text was written ( Egyptian could be written either from right to left or left to right), with the reverse sign indicating subtraction: Nicole Oresme's manuscripts from the 14th century show what may be one of the earliest uses of as a sign for plus. In early 15th century Europe, the letters "P" and "M" were gener ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Real Number
In mathematics, a real number is a number that can be used to measurement, measure a ''continuous'' one-dimensional quantity such as a distance, time, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real number can be almost uniquely represented by an infinite decimal expansion. The real numbers are fundamental in calculus (and more generally in all mathematics), in particular by their role in the classical definitions of limit (mathematics), limits, continuous function, continuity and derivatives. The set of real numbers is mathematical notation, denoted or \mathbb and is sometimes called "the reals". The adjective ''real'' in this context was introduced in the 17th century by René Descartes to distinguish real numbers, associated with physical reality, from imaginary numbers (such as the square roots of ), which seemed like a theoretical contrivance unrelated to physical reality. The real numbers subset, include t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algebra
Algebra () is one of the areas of mathematics, broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics. Elementary algebra deals with the manipulation of variable (mathematics), variables (commonly represented by Roman letters) as if they were numbers and is therefore essential in all applications of mathematics. Abstract algebra is the name given, mostly in mathematical education, education, to the study of algebraic structures such as group (mathematics), groups, ring (mathematics), rings, and field (mathematics), fields (the term is no more in common use outside educational context). Linear algebra, which deals with linear equations and linear mappings, is used for modern presentations of geometry, and has many practical applications (in weather forecasting, for example). There are many areas of mathematics that belong to algebra, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |