|
360 (number)
360 (three hundred [and] sixty) is the natural number following 359 (number), 359 and preceding 361 (number), 361. In mathematics * 360 is the 13th highly composite number and one of only seven numbers such that no number less than twice as much has more divisors; the others are 1, 2, 6, 12 (number), 12, 60 (number), 60, and 2520 (number), 2520 . *360 is also the 6th superior highly composite number, the 6th colossally abundant number, a refactorable number, a 5-smooth number, and a Harshad number in Base ten, decimal since the sum of its digits (9) is a divisor of 360. *360 is divisible by the number of its divisors (24 (number), 24), and it is the smallest number divisible by every natural number from 1 to 10, except 7 (number), 7. Furthermore, one of the divisors of 360 is 72 (number), 72, which is the number of Prime number, primes below it. *360 is the sum of twin primes (179 (number), 179 + 181 (number), 181) and the sum of four consecutive Power of three, powers of thre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compound Of Five Cubes, Gray And Rgby
Compound may refer to: Architecture and built environments * Compound (enclosure), a cluster of buildings having a shared purpose, usually inside a fence or wall ** Compound (fortification), a version of the above fortified with defensive structures * Compound (migrant labour), a hostel for migrant workers such as those historically connected with mines in South Africa * The Compound, an area of Palm Bay, Florida, US * Komboni or compound, a type of slum in Zambia Government and law * Composition (fine), a legal procedure in use after the English Civil War ** Committee for Compounding with Delinquents, an English Civil War institution that allowed Parliament to compound the estates of Royalists * Compounding treason, an offence under the common law of England * Compounding a felony, a previous offense under the common law of England Linguistics * Compound (linguistics), a word that consists of more than one radical element * Compound sentence (linguistics), a type of sentence ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Twin Prime
A twin prime is a prime number that is either 2 less or 2 more than another prime number—for example, either member of the twin prime pair or In other words, a twin prime is a prime that has a prime gap of two. Sometimes the term ''twin prime'' is used for a pair of twin primes; an alternative name for this is prime twin or prime pair. Twin primes become increasingly rare as one examines larger ranges, in keeping with the general tendency of gaps between adjacent primes to become larger as the numbers themselves get larger. However, it is unknown whether there are infinitely many twin primes (the so-called twin prime conjecture) or if there is a largest pair. The breakthrough work of Yitang Zhang in 2013, as well as work by James Maynard, Terence Tao and others, has made substantial progress towards proving that there are infinitely many twin primes, but at present this remains unsolved. Properties Usually the pair is not considered to be a pair of twin primes. Since 2 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Turn (angle)
The turn (symbol tr or pla) is a unit of plane angle measurement that is the measure of a complete angle—the angle subtended by a complete circle at its center. One turn is equal to radians, 360 degrees or 400 gradians. As an angular unit, one turn also corresponds to one cycle (symbol cyc or c) or to one revolution (symbol rev or r). Common related units of frequency are '' cycles per second'' (cps) and '' revolutions per minute'' (rpm). The angular unit of the turn is useful in connection with, among other things, electromagnetic coils (e.g., transformers), rotating objects, and the winding number of curves. Divisions of a turn include the half-turn and quarter-turn, spanning a straight angle and a right angle, respectively; metric prefixes can also be used as in, e.g., centiturns (ctr), milliturns (mtr), etc. In the ISQ, an arbitrary "number of turns" (also known as "number of revolutions" or "number of cycles") is formalized as a dimensionless ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Group
In mathematics, an alternating group is the Group (mathematics), group of even permutations of a finite set. The alternating group on a set of elements is called the alternating group of degree , or the alternating group on letters and denoted by or Basic properties For , the group A''n'' is the commutator subgroup of the symmetric group S''n'' with Index of a subgroup, index 2 and has therefore factorial, ''n''!/2 elements. It is the kernel (algebra), kernel of the signature group homomorphism explained under symmetric group. The group A''n'' is abelian group, abelian if and only if and simple group, simple if and only if or . A5 is the smallest non-abelian simple group, having order of a group, order 60, and thus the smallest non-solvable group. The group A4 has the Klein four-group V as a proper normal subgroup, namely the identity and the double transpositions , that is the kernel of the surjection of A4 onto . We have the exact sequence . In Galois theory, this m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parity Of A Permutation
In mathematics, when ''X'' is a finite set with at least two elements, the permutations of ''X'' (i.e. the bijective functions from ''X'' to ''X'') fall into two classes of equal size: the even permutations and the odd permutations. If any total ordering of ''X'' is fixed, the parity (oddness or evenness) of a permutation \sigma of ''X'' can be defined as the parity of the number of inversions for ''σ'', i.e., of pairs of elements ''x'', ''y'' of ''X'' such that and . The sign, signature, or signum of a permutation ''σ'' is denoted sgn(''σ'') and defined as +1 if ''σ'' is even and −1 if ''σ'' is odd. The signature defines the alternating character of the symmetric group S''n''. Another notation for the sign of a permutation is given by the more general Levi-Civita symbol (''ε''''σ''), which is defined for all maps from ''X'' to ''X'', and has value zero for non-bijective maps. The sign of a permutation can be explicitly expressed as : where ''N''('' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unitary Perfect Number
A unitary perfect number is an integer which is the sum of its positive proper unitary divisors, not including the number itself. (A divisor ''d'' of a number ''n'' is a unitary divisor if ''d'' and ''n''/''d'' share no common factors). The number 6 is the only number that is both a perfect number and a unitary perfect number. Known examples The number 60 is a unitary perfect number because 1, 3, 4, 5, 12, 15, and 20 are its proper unitary divisors, and 1 + 3 + 4 + 5 + 12 + 15 + 20 = 60. The first five, and only known, unitary perfect numbers are: * 6 = 2 \times 3 * 60 = 2^2 \times 3 \times 5 * 90 = 2 \times 3^2 \times 5 * 87360 = 2^6 \times 3 \times 5 \times 7 \times 13, and *146361946186458562560000 = 2^ \times 3 \times 5^4 \times 7 \times 11 \times 13 \times 19 \times 37 \times 79 \times 109 \times 157 \times 313 . The respective sums of their proper unitary divisors are as follows: * 6 = 1 + 2 + 3 * 60 = 1 + 3 + 4 + 5 + 12 + 15 + 20 * 90 = 1 + 2 + 5 + 9 + ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative integers. The set (mathematics), set of all integers is often denoted by the boldface or blackboard bold The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the set of natural numbers, the set of integers \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , 5/4, and Square root of 2, are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler's Totient Function
In number theory, Euler's totient function counts the positive integers up to a given integer that are relatively prime to . It is written using the Greek letter phi as \varphi(n) or \phi(n), and may also be called Euler's phi function. In other words, it is the number of integers in the range for which the greatest common divisor is equal to 1. The integers of this form are sometimes referred to as totatives of . For example, the totatives of are the six numbers 1, 2, 4, 5, 7 and 8. They are all relatively prime to 9, but the other three numbers in this range, 3, 6, and 9 are not, since and . Therefore, . As another example, since for the only integer in the range from 1 to is 1 itself, and . Euler's totient function is a multiplicative function, meaning that if two numbers and are relatively prime, then . This function gives the order of the multiplicative group of integers modulo (the group of units of the ring \Z/n\Z). It is also used for defining the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
243 (number)
243 (two hundred ndforty-three) is the natural number following 242 and preceding 244. Additionally, 243 is: *the only 3-digit number that is a fifth power (35). *a perfect totient number. *the sum of five consecutive prime number A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime ...s (41 + 43 + 47 + 53 + 59). *an 82- gonal number. References Integers {{Num-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
81 (number)
81 (eighty-one) is the natural number following 80 (number), 80and preceding 82 (number), 82. In mathematics 81 is: * the square number, square of 9 (number), 9 and the second fourth-power of a prime; 34. * with an aliquot sum of 40 (number), 40; within an aliquot sequence of three composite numbers (81,40 (number), 40,50 (number), 50,43 (number), 43,1 (number), 1,0) to the Prime in the 43 (number), 43-aliquot tree. * a perfect totient number like all Power of three, powers of three. * a heptagonal number. * an Polygonal number, icosioctagonal number. * a centered octagonal number. * a tribonacci number. * an open meandric number. * the ninth member of the Mian-Chowla sequence. * a palindromic number in bases 8 (1218) and 26 (3326). * a Harshad number in bases 2, 3, 4, 7, 9, 10 and 13. * one of three non-trivial numbers (the other two are 1458 (number), 1458 and 1729 (number), 1729) which, when its digits (in decimal) are added together, produces a sum which, when multiplied by its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
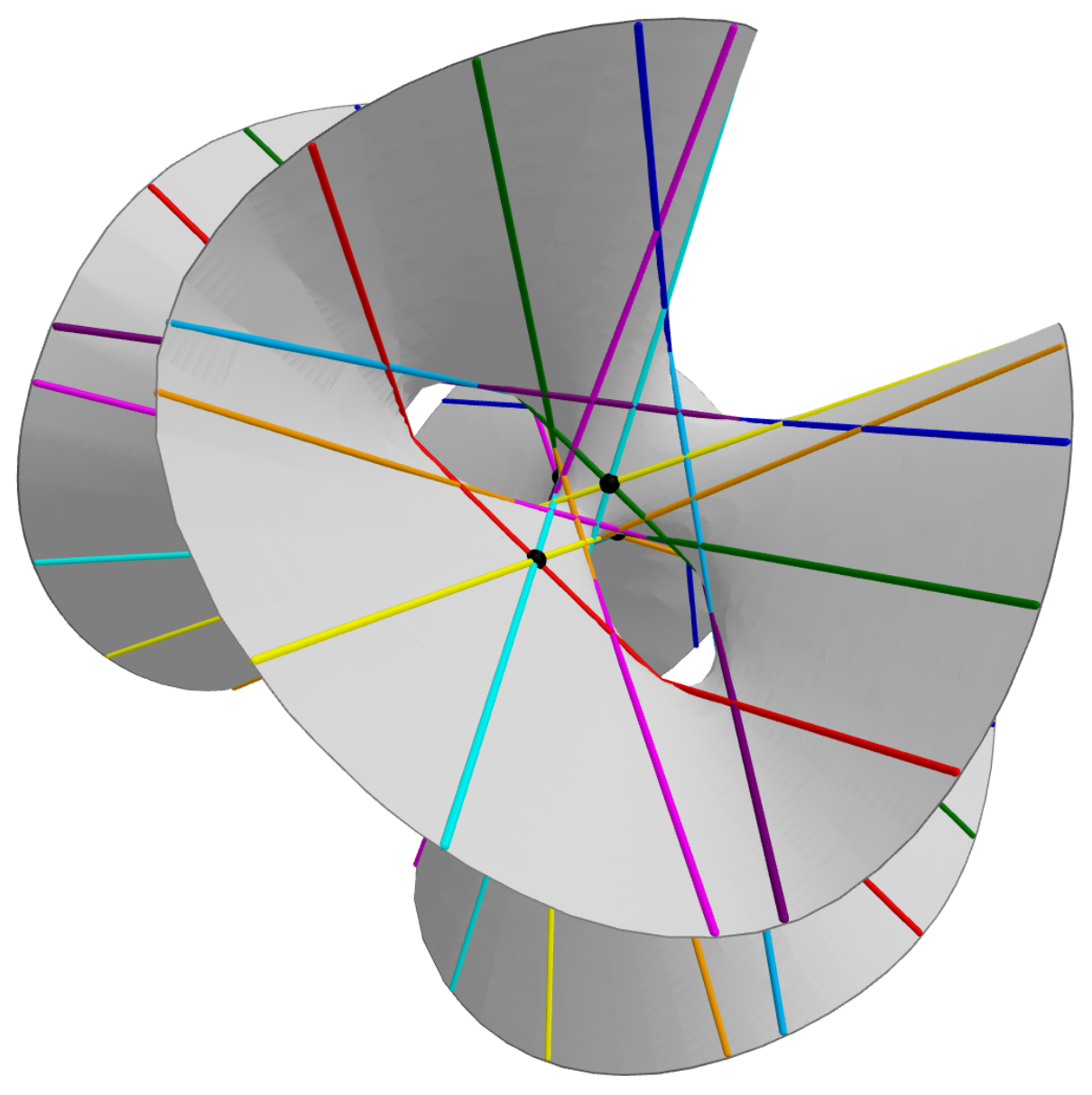
27 (number)
27 (twenty-seven) is the natural number following 26 (number), 26 and preceding 28 (number), 28. Mathematics Including the null-motif, there are 27 distinct Network motif, hypergraph motifs. There are exactly 27 lines on a cubic surface, ''twenty-seven straight lines'' on a smooth cubic surface, which give a basis of the fundamental representation of E6 (mathematics), Lie algebra \mathrm . The unique simple formally real Jordan algebra, the exceptional Jordan algebra of self-adjoint Square matrix, 3 by 3 matrices of quaternions, is 27-dimensional; its automorphism group is the 52-dimensional exceptional Lie algebra \mathrm . There are twenty-seven sporadic groups, if the Tits group, ''non-strict'' group of Lie type \mathrm (with an Faithful representation, irreducible representation that is twice that of \mathrm in 104 dimensions) is included. In Robin's theorem for the Riemann hypothesis, twenty-seven integers fail to hold \sigma(n) < e^\gamma n \log \log n for va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |