|
28 (number)
28 (twenty-eight) is the natural number following 27 (number), 27 and preceding 29 (number), 29. In mathematics Twenty-eight is a composite number and the second perfect number as it is the sum of its proper divisors: 1+2+4+7+14=28. As a perfect number, it is related to the Mersenne prime 7, since 2^\times (2^-1)=28. The next perfect number is 496 (number), 496, the previous being 6 (number), 6. Though perfect, 28 is not the aliquot sum of any other number other than itself; thus, it is not part of a multi-number aliquot sequence. Twenty-eight is the sum of the totient function for the first nine integers. Since the greatest prime factor of 28^+1=785 is 157, which is more than 28 twice, 28 is a Størmer number. Twenty-eight is a harmonic divisor number, a happy number, the 7th triangular number, a hexagonal number, a Leyland number#Leyland number of the second kind, Leyland number of the second kind (2^6-6^2), and a centered nonagonal number. It appears in the Padovan sequ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
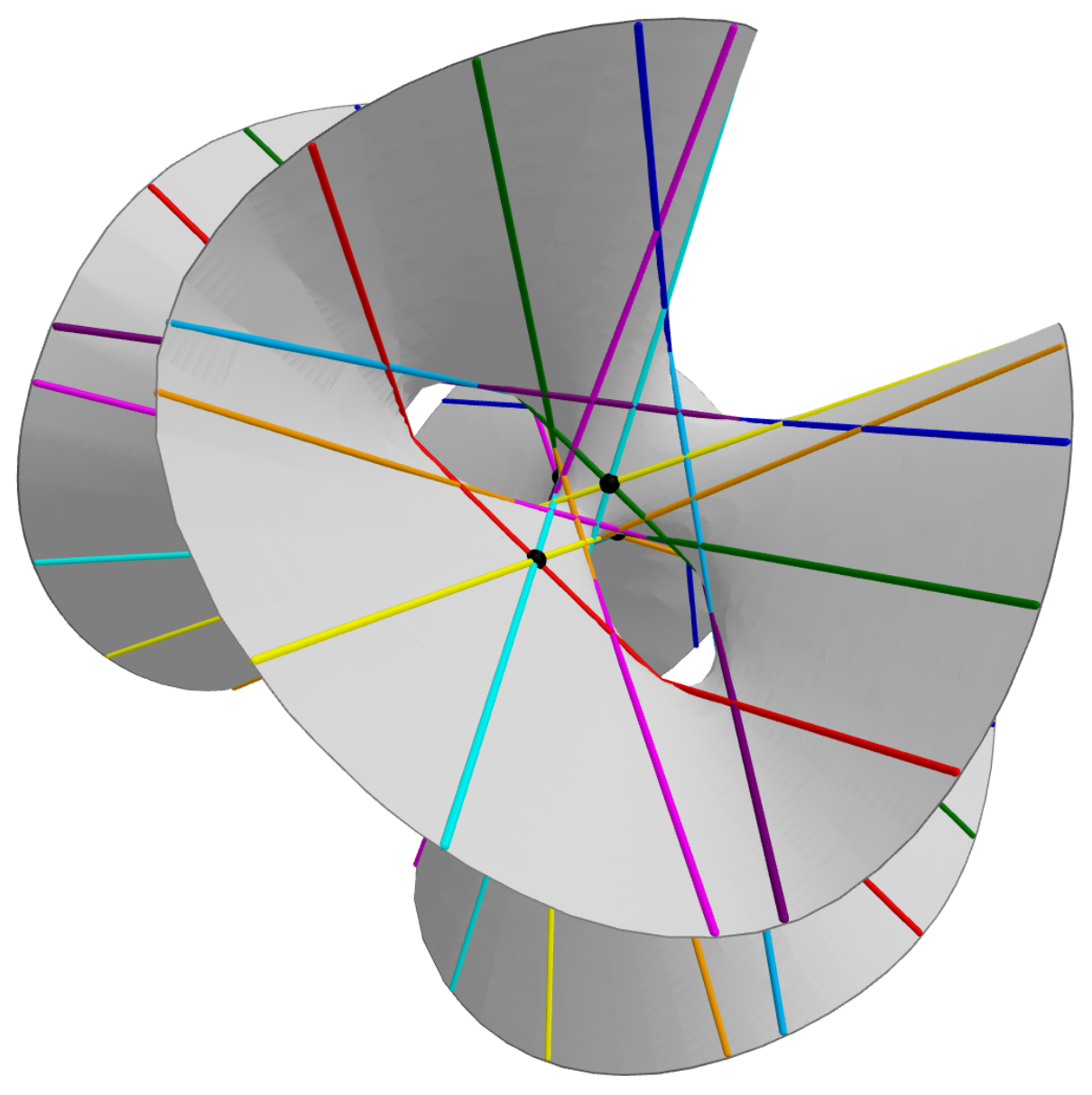
27 (number)
27 (twenty-seven) is the natural number following 26 (number), 26 and preceding 28 (number), 28. Mathematics Including the null-motif, there are 27 distinct Network motif, hypergraph motifs. There are exactly 27 lines on a cubic surface, ''twenty-seven straight lines'' on a smooth cubic surface, which give a basis of the fundamental representation of E6 (mathematics), Lie algebra \mathrm . The unique simple formally real Jordan algebra, the exceptional Jordan algebra of self-adjoint Square matrix, 3 by 3 matrices of quaternions, is 27-dimensional; its automorphism group is the 52-dimensional exceptional Lie algebra \mathrm . There are twenty-seven sporadic groups, if the Tits group, ''non-strict'' group of Lie type \mathrm (with an Faithful representation, irreducible representation that is twice that of \mathrm in 104 dimensions) is included. In Robin's theorem for the Riemann hypothesis, twenty-seven integers fail to hold \sigma(n) < e^\gamma n \log \log n for va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexagonal Number
A hexagonal number is a figurate number. The ''n''th hexagonal number ''h''''n'' is the number of ''distinct'' dots in a pattern of dots consisting of the ''outlines'' of regular hexagons with sides up to n dots, when the hexagons are overlaid so that they share one vertex (geometry), vertex. The formula for the ''n''th hexagonal number :h_n= 2n^2-n = n(2n-1) = \frac. The first few hexagonal numbers are: :1 (number), 1, 6 (number), 6, 15 (number), 15, 28 (number), 28, 45 (number), 45, 66 (number), 66, 91 (number), 91, 120 (number), 120, 153 (number), 153, 190 (number), 190, 231 (number), 231, 276 (number), 276, 325 (number), 325, 378, 435, 496 (number), 496, 561 (number), 561, 630, 703, 780, 861, 946... Every hexagonal number is a triangular number, but only every ''other'' triangular number (the 1st, 3rd, 5th, 7th, etc.) is a hexagonal number. Like a triangular number, the digital root in base 10 of a hexagonal number can only be 1, 3, 6, or 9. The digital root pattern, repe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astrology
Astrology is a range of Divination, divinatory practices, recognized as pseudoscientific since the 18th century, that propose that information about human affairs and terrestrial events may be discerned by studying the apparent positions of Celestial objects in astrology, celestial objects. Different cultures have employed forms of astrology since at least the 2nd millennium BCE, these practices having originated in Calendrical calculation, calendrical systems used to predict seasonal shifts and to interpret celestial cycles as signs of divine communications. Most, if not all, cultures have attached importance to what they observed in the sky, and some—such as the Hindu astrology, Hindus, Chinese astrology, Chinese, and the Maya civilization, Maya—developed elaborate systems for predicting terrestrial events from celestial observations. Western astrology, one of the oldest astrological systems still in use, can trace its roots to 19th–17th century BCE Mesopotamia, fr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Saturn
Saturn is the sixth planet from the Sun and the second largest in the Solar System, after Jupiter. It is a gas giant, with an average radius of about 9 times that of Earth. It has an eighth the average density of Earth, but is over 95 times more massive. Even though Saturn is almost as big as Jupiter, Saturn has less than a third its mass. Saturn orbits the Sun at a distance of , with an orbital period of 29.45 years. Saturn's interior is thought to be composed of a rocky core, surrounded by a deep layer of metallic hydrogen, an intermediate layer of liquid hydrogen and liquid helium, and an outer layer of gas. Saturn has a pale yellow hue, due to ammonia crystals in its upper atmosphere. An electrical current in the metallic hydrogen layer is thought to give rise to Saturn's planetary magnetic field, which is weaker than Earth's, but has a magnetic moment 580 times that of Earth because of Saturn's greater size. Saturn's magnetic field strength is about a twen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magic Number (physics)
In nuclear physics, a magic number is a number of nucleons (either protons or neutrons, separately) such that they are arranged into complete shells within the atomic nucleus. As a result, atomic nuclei with a "magic" number of protons or neutrons are much more stable than other nuclei. The seven most widely recognized magic numbers as of 2019 are 2, 8, 20, 28, 50, 82, and 126. For protons, this corresponds to the elements helium, oxygen, calcium, nickel, tin, lead, and the hypothetical unbihexium, although 126 is so far only known to be a magic number for neutrons. Atomic nuclei consisting of such a magic number of nucleons have a higher average binding energy per nucleon than one would expect based upon predictions such as the semi-empirical mass formula and are hence more stable against nuclear decay. The unusual stability of isotopes having magic numbers means that transuranium elements could theoretically be created with extremely large nuclei and yet not be subject ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals and can be written as . The usual notation for the square of a number is not the product , but the equivalent exponentiation , usually pronounced as " squared". The name ''square'' number comes from the name of the shape. The unit of area is defined as the area of a unit square (). Hence, a square with side length has area . If a square number is represented by ''n'' points, the points can be arranged in rows as a square each side of which has the same number of points as the square root of ''n''; thus, square numbers are a type of Figurate number, figurate numbers (other examples being Cube (algebra), cube numbers and triangular numbers). In the Real number, real number system, square numbers are non-negative. A non-negative integer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable. Definition Given two differentiable manifolds M and N, a Differentiable manifold#Differentiability of mappings between manifolds, continuously differentiable map f \colon M \rightarrow N is a diffeomorphism if it is a bijection and its inverse f^ \colon N \rightarrow M is differentiable as well. If these functions are r times continuously differentiable, f is called a C^r-diffeomorphism. Two manifolds M and N are diffeomorphic (usually denoted M \simeq N) if there is a diffeomorphism f from M to N. Two C^r-differentiable manifolds are C^r-diffeomorphic if there is an r times continuously differentiable bijective map between them whose inverse is also r times continuously differentiable. Diffeomorphisms of subsets of manifolds Given a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kayles
Kayles is a simple impartial game in combinatorial game theory, invented by Henry Dudeney in 1908. Given a row of imagined bowling pins, players take turns to knock out either one pin, or two adjacent pins, until all the pins are gone. Using the notation of octal games, Kayles is denoted 0.77. Rules Kayles is played with a row of tokens, which represent bowling pins. The row may be of any length. The two players alternate; each player, on his or her turn, may remove either any one pin (a ball bowled directly at that pin), or two adjacent pins (a ball bowled to strike both). Under the normal play convention, a player loses when they have no legal move (that is, when all the pins are gone). The game can also be played using misère rules; in this case, the player who cannot move ''wins''. History Kayles was invented by Henry Dudeney.Conway, John H. ''On Numbers and Games.'' Academic Press, 1976. Richard Guy and Cedric Smith were first to completely analyze the normal-pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Uniform Honeycomb
In geometry, a convex uniform honeycomb is a uniform polytope, uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex polyhedron, convex uniform polyhedron, uniform polyhedral cells. Twenty-eight such honeycombs are known: * the familiar cubic honeycomb and 7 truncations thereof; * the alternated cubic honeycomb and 4 truncations thereof; * 10 prismatic forms based on the #Prismatic_stacks, uniform plane tilings (11 if including the cubic honeycomb); * 5 modifications of some of the above by elongation and/or gyration. They can be considered the three-dimensional analogue to the List of uniform planar tilings, uniform tilings of the plane. The Voronoi diagram of any Lattice (group), lattice forms a convex uniform honeycomb in which the cells are zonohedra. History * 1900: Thorold Gosset enumerated the list of semiregular convex polytopes with regular cells (Platonic solids) in his publication ''On the Regular and Semi-Regular Figures in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leonardo Of Pisa
Leonardo Bonacci ( – ), commonly known as Fibonacci, was an Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages". The name he is commonly called, ''Fibonacci'', is first found in a modern source in a 1838 text by the Franco-Italian mathematician Guglielmo Libri and is short for ('son of Bonacci'). However, even as early as 1506, Perizolo, a notary of the Holy Roman Empire, mentions him as "Lionardo Fibonacci". Fibonacci popularized the Indo–Arabic numeral system in the Western world primarily through his composition in 1202 of (''Book of Calculation'') and also introduced Europe to the sequence of Fibonacci numbers, which he used as an example in . Biography Fibonacci was born around 1170 to Guglielmo, an Italian merchant and customs official who directed a trading post in Bugia, modern-day Béjaïa, Algeria. Fibonacci travelled with him as a young boy, and it was in Bugia where he was educate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Keith Number
In recreational mathematics, a Keith number or repfigit number (short for repetitive Fibonacci-like digit) is a natural number n in a given number base b with k digits such that when a sequence is created such that the first k terms are the k digits of n and each subsequent term is the sum of the previous k terms, n is part of the sequence. Keith numbers were introduced by Mike Keith in 1987. They are computationally very challenging to find, with only about 125 known. Definition Let n be a natural number, let k = \lfloor \log_ \rfloor + 1 be the number of digits of n in base b, and let :d_i = \frac be the value of each digit of n. We define the sequence S(i) by a linear recurrence relation. For 0 \leq i bool: """Determine if a number in a particular base is a Keith number.""" if x 0: return True sequence = [] y = x while y > 0: sequence.append(y % b) y = y // b digit_count = len(sequence) sequence.reverse() whi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |