Beam bending on:
[Wikipedia]
[Google]
[Amazon]
 In
In

 In the Euler–Bernoulli theory of slender beams, a major assumption is that 'plane sections remain plane'. In other words, any deformation due to shear across the section is not accounted for (no shear deformation). Also, this linear distribution is only applicable if the maximum stress is less than the
In the Euler–Bernoulli theory of slender beams, a major assumption is that 'plane sections remain plane'. In other words, any deformation due to shear across the section is not accounted for (no shear deformation). Also, this linear distribution is only applicable if the maximum stress is less than the  Compressive and tensile forces develop in the direction of the beam axis under bending loads. These forces induce stresses on the beam. The maximum compressive stress is found at the uppermost edge of the beam while the maximum tensile stress is located at the lower edge of the beam. Since the stresses between these two opposing maxima vary
Compressive and tensile forces develop in the direction of the beam axis under bending loads. These forces induce stresses on the beam. The maximum compressive stress is found at the uppermost edge of the beam while the maximum tensile stress is located at the lower edge of the beam. Since the stresses between these two opposing maxima vary
 For large deformations of the body, the stress in the cross-section is calculated using an extended version of this formula. First the following assumptions must be made:
# Assumption of flat sections – before and after deformation the considered section of body remains flat (i.e., is not swirled).
# Shear and normal stresses in this section that are perpendicular to the normal vector of cross section have no influence on normal stresses that are parallel to this section.
Large bending considerations should be implemented when the bending radius is smaller than ten section heights h:
:
With those assumptions the stress in large bending is calculated as:
:
where
: is the normal force
: is the section
For large deformations of the body, the stress in the cross-section is calculated using an extended version of this formula. First the following assumptions must be made:
# Assumption of flat sections – before and after deformation the considered section of body remains flat (i.e., is not swirled).
# Shear and normal stresses in this section that are perpendicular to the normal vector of cross section have no influence on normal stresses that are parallel to this section.
Large bending considerations should be implemented when the bending radius is smaller than ten section heights h:
:
With those assumptions the stress in large bending is calculated as:
:
where
: is the normal force
: is the section
 In 1921, Timoshenko improved upon the Euler–Bernoulli theory of beams by adding the effect of shear into the beam equation. The kinematic assumptions of the Timoshenko theory are:
* normals to the axis of the beam remain straight after deformation
* there is no change in beam thickness after deformation
However, normals to the axis are not required to remain perpendicular to the axis after deformation.
The equation for the quasistatic bending of a linear elastic, isotropic, homogeneous beam of constant cross-section beam under these assumptions is
:
where is the
In 1921, Timoshenko improved upon the Euler–Bernoulli theory of beams by adding the effect of shear into the beam equation. The kinematic assumptions of the Timoshenko theory are:
* normals to the axis of the beam remain straight after deformation
* there is no change in beam thickness after deformation
However, normals to the axis are not required to remain perpendicular to the axis after deformation.
The equation for the quasistatic bending of a linear elastic, isotropic, homogeneous beam of constant cross-section beam under these assumptions is
:
where is the
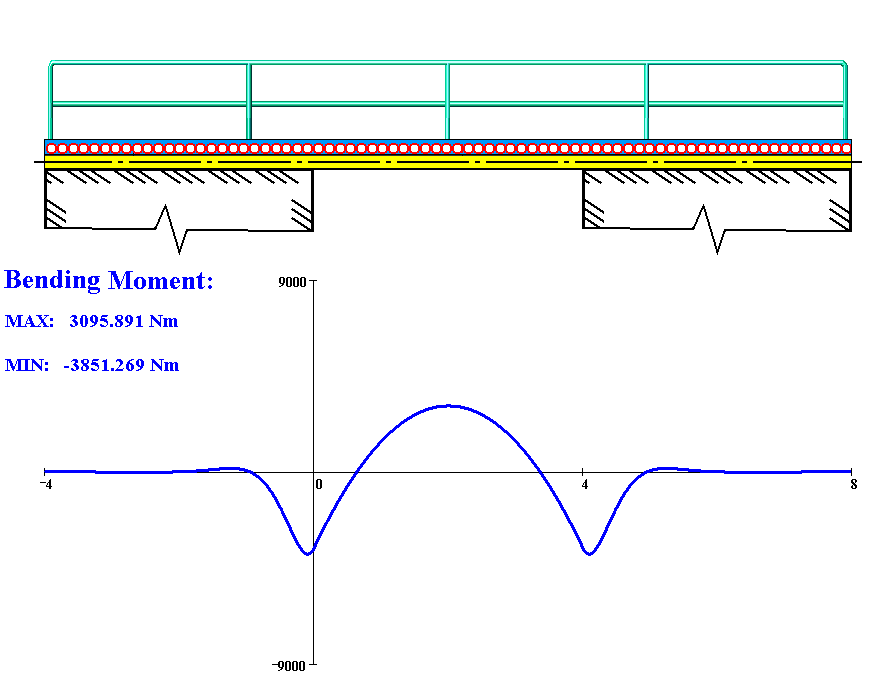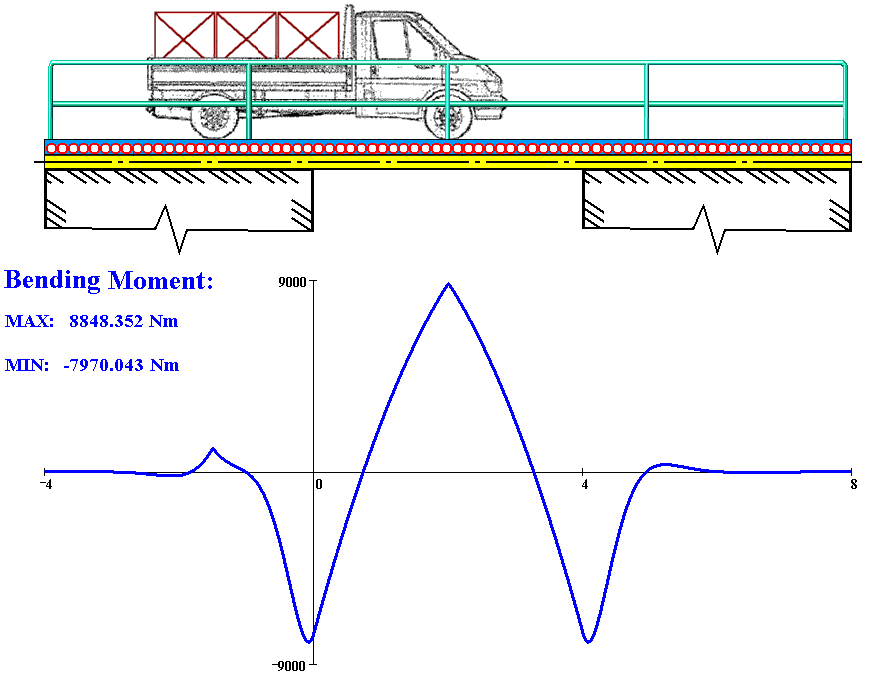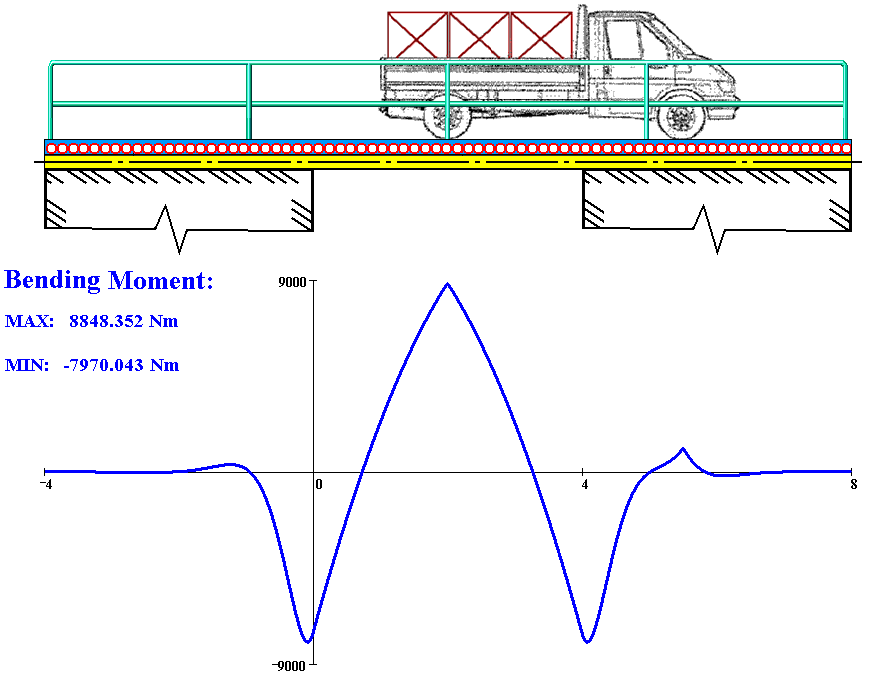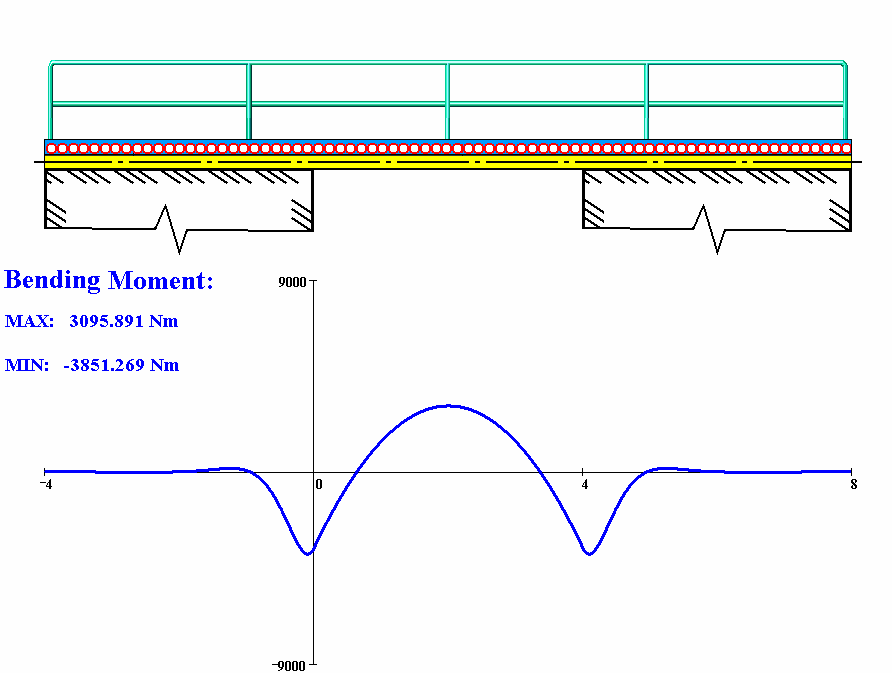
 The defining feature of beams is that one of the dimensions is much ''larger'' than the other two. A structure is called a plate when it is flat and one of its dimensions is much ''smaller'' than the other two. There are several theories that attempt to describe the deformation and stress in a plate under applied loads two of which have been used widely. These are
* the Kirchhoff–Love theory of plates (also called classical plate theory)
* the Mindlin–Reissner plate theory (also called the first-order shear theory of plates)
The defining feature of beams is that one of the dimensions is much ''larger'' than the other two. A structure is called a plate when it is flat and one of its dimensions is much ''smaller'' than the other two. There are several theories that attempt to describe the deformation and stress in a plate under applied loads two of which have been used widely. These are
* the Kirchhoff–Love theory of plates (also called classical plate theory)
* the Mindlin–Reissner plate theory (also called the first-order shear theory of plates)
File:Drum vibration mode01.gif, mode ''k'' = 0, ''p'' = 1
File:Drum vibration mode02.gif, mode ''k'' = 0, ''p'' = 2
File:Drum vibration mode12.gif, mode ''k'' = 1, ''p'' = 2
Flexure formulae
Beam stress & deflection, beam deflection tables
{{Topics in continuum mechanics Statics Elasticity (physics) Structural system Deformation (mechanics)
 In
In applied mechanics
Applied mechanics is the branch of science concerned with the motion of any substance that can be experienced or perceived by humans without the help of instruments. In short, when mechanics concepts surpass being theoretical and are applied and e ...
, bending (also known as flexure) characterizes the behavior of a slender structural
A structure is an arrangement and organization of interrelated elements in a material object or system, or the object or system so organized. Material structures include man-made objects such as buildings and machines and natural objects such ...
element subjected to an external load applied perpendicularly to a longitudinal axis of the element.
The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically 1/10 or less, of the other two.Boresi, A. P. and Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced mechanics of materials, John Wiley and Sons, New York. When the length is considerably longer than the width and the thickness, the element is called a beam. For example, a closet
A closet (especially in North American usage) is an enclosed space, with a door, used for storage, particularly that of clothes. ''Fitted closets'' are built into the walls of the house so that they take up no apparent space in the room. Closet ...
rod sagging under the weight of clothes on clothes hanger
A clothes hanger, coat hanger, or coathanger, is a hanging device in the shape/contour of:
* Human shoulders designed to facilitate the hanging of a coat, jacket, sweater, shirt, blouse or dress in a manner that prevents wrinkles, with a lowe ...
s is an example of a beam experiencing bending. On the other hand, a shell
Shell may refer to:
Architecture and design
* Shell (structure), a thin structure
** Concrete shell, a thin shell of concrete, usually with no interior columns or exterior buttresses
** Thin-shell structure
Science Biology
* Seashell, a hard o ...
is a structure of any geometric form where the length and the width are of the same order of magnitude but the thickness of the structure (known as the 'wall') is considerably smaller. A large diameter, but thin-walled, short tube supported at its ends and loaded laterally is an example of a shell experiencing bending.
In the absence of a qualifier, the term ''bending'' is ambiguous because bending can occur locally in all objects. Therefore, to make the usage of the term more precise, engineers refer to a specific object such as; the ''bending of rods'', the ''bending of beams'', the ''bending of plates
Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of ...
'', Timoshenko, S. and Woinowsky-Krieger, S., 1959, Theory of plates and shells, McGraw-Hill. the '' bending of shells''Libai, A. and Simmonds, J. G., 1998, The nonlinear theory of elastic shells, Cambridge University Press. and so on.
Quasi-static bending of beams
A beam deforms and stresses develop inside it when a transverse load is applied on it. In the quasi-static case, the amount of bendingdeflection
Deflection or deflexion may refer to:
Board games
* Deflection (chess), a tactic that forces an opposing chess piece to leave a square
* Khet (game), formerly ''Deflexion'', an Egyptian-themed chess-like game using lasers
Mechanics
* Deflection ...
and the stresses that develop are assumed not to change over time. In a horizontal beam supported at the ends and loaded downwards in the middle, the material at the over-side of the beam is compressed while the material at the underside is stretched. There are two forms of internal stresses caused by lateral loads:
* Shear stress
Shear stress, often denoted by (Greek: tau), is the component of stress coplanar with a material cross section. It arises from the shear force, the component of force vector parallel to the material cross section. ''Normal stress'', on the ...
parallel to the lateral loading plus complementary shear stress on planes perpendicular to the load direction;
* Direct compressive stress
In long, slender structural elements — such as columns or truss bars — an increase of compressive force ''F'' leads to structural failure due to buckling at lower stress than the compressive strength.
Compressive stress has stress units (fo ...
in the upper region of the beam, and direct tensile stress
In continuum mechanics, stress is a physical quantity. It is a quantity that describes the magnitude of forces that cause deformation. Stress is defined as ''force per unit area''. When an object is pulled apart by a force it will cause elonga ...
in the lower region of the beam.
These last two forces form a couple
Couple or couples may refer to :
Basic meaning
*Couple (app), a mobile app which provides a mobile messaging service for two people
*Couple (mechanics), a system of forces with a resultant moment but no resultant force
*Couple (relationship), tw ...
or moment as they are equal in magnitude and opposite in direction. This bending moment
In solid mechanics, a bending moment is the reaction induced in a structural element when an external force or moment is applied to the element, causing the element to bend. The most common or simplest structural element subjected to bending mo ...
resists the sagging deformation characteristic of a beam experiencing bending. The stress distribution in a beam can be predicted quite accurately when some simplifying assumptions are used.
Euler–Bernoulli bending theory
yield stress
In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and w ...
of the material. For stresses that exceed yield, refer to article plastic bending Plastic bending is a nonlinear behavior particular to members made of ductile materials that frequently achieve much greater ultimate bending strength than indicated by a linear elastic bending analysis. In both the plastic and elastic bending ana ...
. At yield, the maximum stress experienced in the section (at the furthest points from the neutral axis
The neutral axis is an axis in the cross section of a beam (a member resisting bending) or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the ne ...
of the beam) is defined as the flexural strength
Flexural strength, also known as modulus of rupture, or bend strength, or transverse rupture strength is a material property, defined as the stress in a material just before it yields in a flexure test. The transverse bending test is most frequ ...
.
Consider beams where the following are true:
* The beam is originally straight and slender, and any taper is slight
* The material is isotropic (or orthotropic), linear elastic, and homogeneous across any cross section (but not necessarily along its length)
* Only small deflections are considered
In this case, the equation describing beam deflection () can be approximated as:
:
where the second derivative of its deflected shape with respect to is interpreted as its curvature, is the Young's modulus
Young's modulus E, the Young modulus, or the modulus of elasticity in tension or compression (i.e., negative tension), is a mechanical property that measures the tensile or compressive stiffness of a solid material when the force is applied le ...
, is the area moment of inertia
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The ...
of the cross-section, and is the internal bending moment in the beam.
If, in addition, the beam is homogeneous along its length as well, and not tapered (i.e. constant cross section), and deflects under an applied transverse load , it can be shown that:
:
This is the Euler–Bernoulli equation for beam bending.
After a solution for the displacement of the beam has been obtained, the bending moment () and shear force () in the beam can be calculated using the relations
:
Simple beam bending is often analyzed with the Euler–Bernoulli beam equation. The conditions for using simple bending theory are:
# The beam is subject to pure bending Pure bending ( Theory of simple bending) is a condition of stress where a bending moment is applied to a beam without the simultaneous presence of axial, shear, or torsional forces.
Pure bending occurs only under a constant bending moment (M) sinc ...
. This means that the shear force is zero, and that no torsional or axial loads are present.
# The material is isotropic (or orthotropic) and homogeneous.
# The material obeys Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of ...
(it is linearly elastic and will not deform plastically).
# The beam is initially straight with a cross section that is constant throughout the beam length.
# The beam has an axis of symmetry in the plane of bending.
# The proportions of the beam are such that it would fail by bending rather than by crushing, wrinkling or sideways buckling
In structural engineering, buckling is the sudden change in shape ( deformation) of a structural component under load, such as the bowing of a column under compression or the wrinkling of a plate under shear. If a structure is subjected to a ...
.
# Cross-sections of the beam remain plane during bending.
linear
Linearity is the property of a mathematical relationship ('' function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear ...
ly, there therefore exists a point on the linear path between them where there is no bending stress. The locus
Locus (plural loci) is Latin for "place". It may refer to:
Entertainment
* Locus (comics), a Marvel Comics mutant villainess, a member of the Mutant Liberation Front
* ''Locus'' (magazine), science fiction and fantasy magazine
** ''Locus Award' ...
of these points is the neutral axis. Because of this area with no stress and the adjacent areas with low stress, using uniform cross section beams in bending is not a particularly efficient means of supporting a load as it does not use the full capacity of the beam until it is on the brink of collapse. Wide-flange beams ( -beams) and truss
A truss is an assembly of ''members'' such as beams, connected by ''nodes'', that creates a rigid structure.
In engineering, a truss is a structure that "consists of two-force members only, where the members are organized so that the assembl ...
girder
A girder () is a support beam used in construction. It is the main horizontal support of a structure which supports smaller beams. Girders often have an I-beam cross section composed of two load-bearing ''flanges'' separated by a stabilizing ...
s effectively address this inefficiency as they minimize the amount of material in this under-stressed region.
The classic formula for determining the bending stress in a beam under simple bending is:Gere, J. M. and Timoshenko, S.P., 1997, Mechanics of Materials, PWS Publishing Company.
:
where
* is the bending stress
* – the moment about the neutral axis
* – the perpendicular distance to the neutral axis
* – the second moment of area
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The ...
about the neutral axis ''z''.
* - the Resistance Moment about the neutral axis ''z''.
Extensions of Euler-Bernoulli beam bending theory
Plastic bending
The equation is valid only when the stress at the extreme fiber (i.e., the portion of the beam farthest from the neutral axis) is below theyield stress
In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and w ...
of the material from which it is constructed. At higher loadings the stress distribution becomes non-linear, and ductile materials will eventually enter a ''plastic hinge'' state where the magnitude of the stress is equal to the yield stress everywhere in the beam, with a discontinuity at the neutral axis where the stress changes from tensile to compressive. This plastic hinge state is typically used as a limit state
Limit State Design (LSD), also known as Load And Resistance Factor Design (LRFD), refers to a design method used in structural engineering. A limit state is a condition of a structure beyond which it no longer fulfills the relevant design criteria ...
in the design of steel structures.
Complex or asymmetrical bending
The equation above is only valid if the cross-section is symmetrical. For homogeneous beams with asymmetrical sections, the maximum bending stress in the beam is given by : where are the coordinates of a point on the cross section at which the stress is to be determined as shown to the right, and are the bending moments about the y and zcentroid
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any ...
axes, and are the second moments of area (distinct from moments of inertia) about the y and z axes, and is the product of moments of area. Using this equation it is possible to calculate the bending stress at any point on the beam cross section regardless of moment orientation or cross-sectional shape. Note that do not change from one point to another on the cross section.
Large bending deformation
area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape or planar lamina, while '' surface area'' refers to the area of an ope ...
: is the bending moment
: is the local bending radius (the radius of bending at the current section)
: is the area moment of inertia along the ''x''-axis, at the place (see Steiner's theorem)
: is the position along ''y''-axis on the section area in which the stress is calculated.
When bending radius approaches infinity and , the original formula is back:
:.
Timoshenko bending theory
area moment of inertia
The second moment of area, or second area moment, or quadratic moment of area and also known as the area moment of inertia, is a geometrical property of an area which reflects how its points are distributed with regard to an arbitrary axis. The ...
of the cross-section, is the cross-sectional area, is the shear modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain:
:G \ \stackre ...
, is a shear correction factor, and is an applied transverse load. For materials with Poisson's ratio
In materials science and solid mechanics, Poisson's ratio \nu ( nu) is a measure of the Poisson effect, the deformation (expansion or contraction) of a material in directions perpendicular to the specific direction of loading. The value of Po ...
s () close to 0.3, the shear correction factor for a rectangular cross-section is approximately
:
The rotation () of the normal is described by the equation
:
The bending moment () and the shear force () are given by
:
Beams on elastic foundations
According to Euler–Bernoulli, Timoshenko or other bending theories, the beams on elastic foundations can be explained. In some applications such as rail tracks, foundation of buildings and machines, ships on water, roots of plants etc., the beam subjected to loads is supported on continuous elastic foundations (i.e. the continuous reactions due to external loading is distributed along the length of the beam)
Dynamic bending of beams
The dynamic bending of beams,Han, S. M, Benaroya, H. and Wei, T., 1999, "Dynamics of transversely vibrating beams using four engineering theories," ''Journal of Sound and Vibration'', vol. 226, no. 5, pp. 935–988. also known as flexural vibrations of beams, was first investigated by Daniel Bernoulli in the late 18th century. Bernoulli's equation of motion of a vibrating beam tended to overestimate thenatural frequencies
The fundamental frequency, often referred to simply as the ''fundamental'', is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the lowest partial present. In ...
of beams and was improved marginally by Rayleigh in 1877 by the addition of a mid-plane rotation. In 1921 Stephen Timoshenko
Stepan Prokofyevich Timoshenko (russian: Степан Прокофьевич Тимошенко, p=sʲtʲɪˈpan prɐˈkofʲjɪvʲɪtɕ tʲɪmɐˈʂɛnkə; uk, Степан Прокопович Тимошенко, Stepan Prokopovych Tymoshenko; ...
improved the theory further by incorporating the effect of shear on the dynamic response of bending beams. This allowed the theory to be used for problems involving high frequencies of vibration where the dynamic Euler–Bernoulli theory is inadequate. The Euler-Bernoulli and Timoshenko theories for the dynamic bending of beams continue to be used widely by engineers.
Euler–Bernoulli theory
The Euler–Bernoulli equation for the dynamic bending of slender, isotropic, homogeneous beams of constant cross-section under an applied transverse load isThomson, W. T., 1981, Theory of Vibration with Applications : where is the Young's modulus, is the area moment of inertia of the cross-section, is the deflection of the neutral axis of the beam, and is mass per unit length of the beam.Free vibrations
For the situation where there is no transverse load on the beam, the bending equation takes the form : Free, harmonic vibrations of the beam can then be expressed as : and the bending equation can be written as : The general solution of the above equation is : where are constants andTimoshenko–Rayleigh theory
In 1877, Rayleigh proposed an improvement to the dynamic Euler–Bernoulli beam theory by including the effect of rotational inertia of the cross-section of the beam. Timoshenko improved upon that theory in 1922 by adding the effect of shear into the beam equation. Shear deformations of the normal to the mid-surface of the beam are allowed in the Timoshenko–Rayleigh theory. The equation for the bending of a linear elastic, isotropic, homogeneous beam of constant cross-section under these assumptions isRosinger, H. E. and Ritchie, I. G., 1977, ''On Timoshenko's correction for shear in vibrating isotropic beams,'' J. Phys. D: Appl. Phys., vol. 10, pp. 1461–1466. : where is the polar moment of inertia of the cross-section, is the mass per unit length of the beam, is the density of the beam, is the cross-sectional area, is the shear modulus, and is a shear correction factor. For materials with Poisson's ratios () close to 0.3, the shear correction factor are approximately :Free vibrations
For free, harmonic vibrations the Timoshenko–Rayleigh equations take the form : This equation can be solved by noting that all the derivatives of must have the same form to cancel out and hence as solution of the form may be expected. This observation leads to the characteristic equation : The solutions of thisquartic equation
In mathematics, a quartic equation is one which can be expressed as a ''quartic function'' equaling zero. The general form of a quartic equation is
:ax^4+bx^3+cx^2+dx+e=0 \,
where ''a'' ≠ 0.
The quartic is the highest order polynomi ...
are
:
where
:
The general solution of the Timoshenko-Rayleigh beam equation for free vibrations can then be written as
:
Quasistatic bending of plates
Kirchhoff–Love theory of plates
The assumptions of Kirchhoff–Love theory are * straight lines normal to the mid-surface remain straight after deformation * straight lines normal to the mid-surface remain normal to the mid-surface after deformation * the thickness of the plate does not change during a deformation. These assumptions imply that : where is the displacement of a point in the plate and is the displacement of the mid-surface. The strain-displacement relations are : The equilibrium equations are : where is an applied load normal to the surface of the plate. In terms of displacements, the equilibrium equations for an isotropic, linear elastic plate in the absence of external load can be written as : In direct tensor notation, :Mindlin–Reissner theory of plates
The special assumption of this theory is that normals to the mid-surface remain straight and inextensible but not necessarily normal to the mid-surface after deformation. The displacements of the plate are given by : where are the rotations of the normal. The strain-displacement relations that result from these assumptions are : where is a shear correction factor. The equilibrium equations are : where :Dynamic bending of plates
Dynamics of thin Kirchhoff plates
The dynamic theory of plates determines the propagation of waves in the plates, and the study of standing waves and vibration modes. The equations that govern the dynamic bending of Kirchhoff plates are : where, for a plate with density , : and : The figures below show some vibrational modes of a circular plate.See also
*Bending moment
In solid mechanics, a bending moment is the reaction induced in a structural element when an external force or moment is applied to the element, causing the element to bend. The most common or simplest structural element subjected to bending mo ...
* Bending Machine (flat metal bending)
* Brake (sheet metal bending)
A brake is a metalworking machine that allows the bending of sheet metal. A cornice brake only allows for simple bends and creases, while a box-and-pan brake also allows one to form box and pan shapes. It is also known as a bending machine or b ...
* Brazier effect
* Bending of plates
Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of ...
* Bending (metalworking)
Bending is a manufacturing process that produces a V-shape, U-shape, or channel shape along a straight axis in ductile materials, most commonly sheet metal.Manufacturing Processes Reference Guide, Industrial Press Inc., 1994. Commonly used equ ...
* Continuum mechanics
* Contraflexure
* Deflection (engineering)
In structural engineering, deflection is the degree to which a part of a structural element is displaced under a load (because it deforms). It may refer to an angle or a distance.
The deflection distance of a member under a load can be calcul ...
* Flexure bearing
A flexure bearing is a category of flexure which is engineered to be compliant in one or more angular degrees of freedom. Flexure bearings are often part of compliant mechanisms. Flexure bearings serve much of the same function as conventional ...
* List of area moments of inertia
* Pipe bending
* Shear and moment diagram
Shear force and bending moment diagrams are analytical tools used in conjunction with structural analysis to help perform structural design by determining the value of shear forces and bending moments at a given point of a structural element su ...
* Shear strength
In engineering, shear strength is the strength of a material or component against the type of yield or structural failure when the material or component fails in shear. A shear load is a force that tends to produce a sliding failure on a materi ...
* Sandwich theory
Sandwich theoryPlantema, F, J., 1966, Sandwich Construction: The Bending and Buckling of Sandwich Beams, Plates, and Shells, Jon Wiley and Sons, New York.Zenkert, D., 1995, An Introduction to Sandwich Construction, Engineering Materials Advisory S ...
* Vibration
Vibration is a mechanical phenomenon whereby oscillations occur about an equilibrium point. The word comes from Latin ''vibrationem'' ("shaking, brandishing"). The oscillations may be periodic, such as the motion of a pendulum—or random, su ...
* Vibration of plates
The vibration of plates is a special case of the more general problem of mechanical vibrations. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is ...
References
External links
Flexure formulae
Beam stress & deflection, beam deflection tables
{{Topics in continuum mechanics Statics Elasticity (physics) Structural system Deformation (mechanics)