Improper integral on:
[Wikipedia]
[Google]
[Amazon]
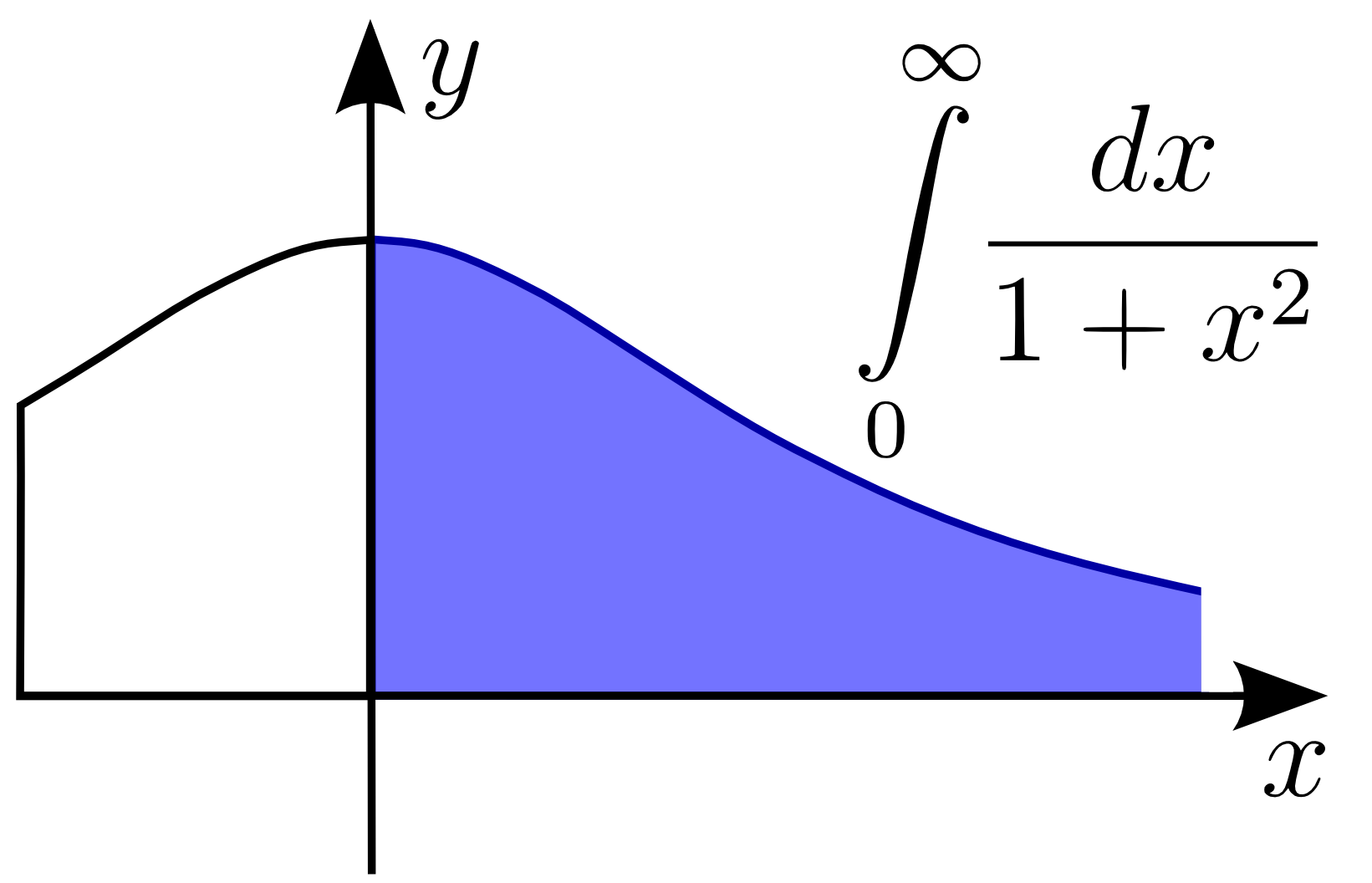
 In
In
 Sometimes integrals may have two singularities where they are improper. Consider, for example, the function integrated from 0 to (shown right). At the lower bound, as goes to 0 the function goes to , and the upper bound is itself , though the function goes to 0. Thus this is a doubly improper integral. Integrated, say, from 1 to 3, an ordinary Riemann sum suffices to produce a result of /6. To integrate from 1 to , a Riemann sum is not possible. However, any finite upper bound, say (with ), gives a well-defined result, . This has a finite limit as goes to infinity, namely /2. Similarly, the integral from 1/3 to 1 allows a Riemann sum as well, coincidentally again producing /6. Replacing 1/3 by an arbitrary positive value (with ) is equally safe, giving . This, too, has a finite limit as goes to zero, namely /2. Combining the limits of the two fragments, the result of this improper integral is
:
This process does not guarantee success; a limit might fail to exist, or might be infinite. For example, over the bounded interval from 0 to 1 the integral of does not converge; and over the unbounded interval from 1 to the integral of does not converge.
Sometimes integrals may have two singularities where they are improper. Consider, for example, the function integrated from 0 to (shown right). At the lower bound, as goes to 0 the function goes to , and the upper bound is itself , though the function goes to 0. Thus this is a doubly improper integral. Integrated, say, from 1 to 3, an ordinary Riemann sum suffices to produce a result of /6. To integrate from 1 to , a Riemann sum is not possible. However, any finite upper bound, say (with ), gives a well-defined result, . This has a finite limit as goes to infinity, namely /2. Similarly, the integral from 1/3 to 1 allows a Riemann sum as well, coincidentally again producing /6. Replacing 1/3 by an arbitrary positive value (with ) is equally safe, giving . This, too, has a finite limit as goes to zero, namely /2. Combining the limits of the two fragments, the result of this improper integral is
:
This process does not guarantee success; a limit might fail to exist, or might be infinite. For example, over the bounded interval from 0 to 1 the integral of does not converge; and over the unbounded interval from 1 to the integral of does not converge.
 It might also happen that an integrand is unbounded near an interior point, in which case the integral must be split at that point. For the integral as a whole to converge, the limit integrals on both sides must exist and must be bounded. For example:
:
But the similar integral
:
cannot be assigned a value in this way, as the integrals above and below zero do not independently converge. (However, see
It might also happen that an integrand is unbounded near an interior point, in which case the integral must be split at that point. For the integral as a whole to converge, the limit integrals on both sides must exist and must be bounded. For example:
:
But the similar integral
:
cannot be assigned a value in this way, as the integrals above and below zero do not independently converge. (However, see

 In some cases, the integral
:
can be defined as an integral (a
In some cases, the integral
:
can be defined as an integral (a
Numerical Methods to Solve Improper Integrals
at Holistic Numerical Methods Institute {{integral Integral calculus

 In
In mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limits, and related theories, such as differentiation, integration, measure, infinite sequences, series, and analytic functions.
These theories are usually studied ...
, an improper integral is the limit
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
of a definite integral
In mathematics, an integral assigns numbers to functions in a way that describes displacement, area, volume, and other concepts that arise by combining infinitesimal data. The process of finding integrals is called integration. Along with ...
as an endpoint of the interval(s) of integration approaches either a specified real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
or positive or negative infinity
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions am ...
; or in some instances as both endpoints approach limits. Such an integral is often written symbolically just like a standard definite integral, in some cases with ''infinity'' as a limit of integration.
Specifically, an improper integral is a limit of the form:
:
or
:
in which one takes a limit in one or the other (or sometimes both) endpoints .
By abuse of notation
In mathematics, abuse of notation occurs when an author uses a mathematical notation in a way that is not entirely formally correct, but which might help simplify the exposition or suggest the correct intuition (while possibly minimizing errors a ...
, improper integrals are often written symbolically just like standard definite integrals, perhaps with ''infinity'' among the limits of integration. When the definite integral exists (in the sense of either the Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of G� ...
or the more powerful Lebesgue integral
In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the -axis. The Lebesgue integral, named after French mathematician Henri Lebe ...
), this ambiguity is resolved as both the proper and improper integral will coincide in value.
Often one is able to compute values for improper integrals, even when the function is not integrable in the conventional sense (as a Riemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of G� ...
, for instance) because of a singularity in the function or because one of the bounds of integration is infinite.
Examples
The original definition of theRiemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of G� ...
does not apply to a function such as on the interval , because in this case the domain of integration is unbounded. However, the Riemann integral can often be extended by continuity, by defining the improper integral instead as a limit
Limit or Limits may refer to:
Arts and media
* ''Limit'' (manga), a manga by Keiko Suenobu
* ''Limit'' (film), a South Korean film
* Limit (music), a way to characterize harmony
* "Limit" (song), a 2016 single by Luna Sea
* "Limits", a 2019 ...
:
The narrow definition of the Riemann integral also does not cover the function on the interval . The problem here is that the integrand is unbounded in the domain of integration (the definition requires that both the domain of integration and the integrand be bounded). However, the improper integral does exist if understood as the limit
:
Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.
Formulation
Depending on the type of singularity in the integrand ...
.)
Convergence of the integral
An improper integral converges if the limit defining it exists. Thus for example one says that the improper integral : exists and is equal to ''L'' if the integrals under the limit exist for all sufficiently large ''t'', and the value of the limit is equal to ''L''. It is also possible for an improper integral to diverge to infinity. In that case, one may assign the value of ∞ (or −∞) to the integral. For instance : However, other improper integrals may simply diverge in no particular direction, such as : which does not exist, even as an extended real number. This is called divergence by oscillation. A limitation of the technique of improper integration is that the limit must be taken with respect to one endpoint at a time. Thus, for instance, an improper integral of the form : can be defined by taking two separate limits; to wit : provided the double limit is finite. It can also be defined as a pair of distinct improper integrals of the first kind: : where ''c'' is any convenient point at which to start the integration. This definition also applies when one of these integrals is infinite, or both if they have the same sign. An example of an improper integral where both endpoints are infinite is theGaussian integral
The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function f(x) = e^ over the entire real line. Named after the German mathematician Carl Friedrich Gauss, the integral is
\int_^\infty e^\,dx = \s ...
An example which evaluates to infinity is But one cannot even define other integrals of this kind unambiguously, such as since the double limit is infinite and the two-integral method
:
yields In this case, one can however define an improper integral in the sense of Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.
Formulation
Depending on the type of singularity in the integrand ...
:
:
The questions one must address in determining an improper integral are:
*Does the limit exist?
*Can the limit be computed?
The first question is an issue of mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limits, and related theories, such as differentiation, integration, measure, infinite sequences, series, and analytic functions.
These theories are usually studied ...
. The second one can be addressed by calculus techniques, but also in some cases by contour integration
In the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.
Contour integration is closely related to the calculus of residues, a method of complex analysis.
...
, Fourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed ...
s and other more advanced methods.
Types of integrals
There is more than one theory of integration. From the point of view of calculus, theRiemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. It was presented to the faculty at the University of G� ...
theory is usually assumed as the default theory. In using improper integrals, it can matter which integration theory is in play.
* For the Riemann integral (or the Darboux integral
In the branch of mathematics known as real analysis, the Darboux integral is constructed using Darboux sums and is one possible definition of the integral of a function. Darboux integrals are equivalent to Riemann integrals, meaning that a functi ...
, which is equivalent to it), improper integration is necessary ''both'' for unbounded intervals (since one cannot divide the interval into finitely many subintervals of finite length) ''and'' for unbounded functions with finite integral (since, supposing it is unbounded above, then the upper integral will be infinite, but the lower integral will be finite).
* The Lebesgue integral
In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the -axis. The Lebesgue integral, named after French mathematician Henri Lebe ...
deals differently with unbounded domains and unbounded functions, so that often an integral which only exists as an improper Riemann integral will exist as a (proper) Lebesgue integral, such as . On the other hand, there are also integrals that have an improper Riemann integral but do not have a (proper) Lebesgue integral, such as . The Lebesgue theory does not see this as a deficiency: from the point of view of measure theory
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures (length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many simila ...
, and cannot be defined satisfactorily. In some situations, however, it may be convenient to employ improper Lebesgue integrals as is the case, for instance, when defining the Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.
Formulation
Depending on the type of singularity in the integrand ...
. The Lebesgue integral is more or less essential in the theoretical treatment of the Fourier transform
A Fourier transform (FT) is a mathematical transform that decomposes functions into frequency components, which are represented by the output of the transform as a function of frequency. Most commonly functions of time or space are transformed ...
, with pervasive use of integrals over the whole real line.
* For the Henstock–Kurzweil integral, improper integration ''is not necessary'', and this is seen as a strength of the theory: it encompasses all Lebesgue integrable and improper Riemann integrable functions.
Improper Riemann integrals and Lebesgue integrals

 In some cases, the integral
:
can be defined as an integral (a
In some cases, the integral
:
can be defined as an integral (a Lebesgue integral
In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the -axis. The Lebesgue integral, named after French mathematician Henri Lebe ...
, for instance) without reference to the limit
:
but cannot otherwise be conveniently computed. This often happens when the function ''f'' being integrated from ''a'' to ''c'' has a vertical asymptote at ''c'', or if ''c'' = ∞ (see Figures 1 and 2). In such cases, the improper Riemann integral allows one to calculate the Lebesgue integral of the function. Specifically, the following theorem holds :
* If a function ''f'' is Riemann integrable on 'a'',''b''for every ''b'' ≥ ''a'', and the partial integrals
::
:are bounded as ''b'' → ∞, then the improper Riemann integrals
::
:both exist. Furthermore, ''f'' is Lebesgue integrable on [''a'', ∞), and its Lebesgue integral is equal to its improper Riemann integral.
For example, the integral
:
can be interpreted alternatively as the improper integral
:
or it may be interpreted instead as a Lebesgue integral
In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the -axis. The Lebesgue integral, named after French mathematician Henri Lebe ...
over the set (0, ∞). Since both of these kinds of integral agree, one is free to choose the first method to calculate the value of the integral, even if one ultimately wishes to regard it as a Lebesgue integral. Thus improper integrals are clearly useful tools for obtaining the actual values of integrals.
In other cases, however, a Lebesgue integral between finite endpoints may not even be defined, because the integrals of the positive and negative parts of ''f'' are both infinite, but the improper Riemann integral may still exist. Such cases are "properly improper" integrals, i.e. their values cannot be defined except as such limits. For example,
:
cannot be interpreted as a Lebesgue integral, since
:
But is nevertheless integrable between any two finite endpoints, and its integral between 0 and ∞ is usually understood as the limit of the integral:
:
Singularities
One can speak of the ''singularities'' of an improper integral, meaning those points of the extended real number line at which limits are used.Cauchy principal value
Consider the difference in values of two limits: : : The former is the Cauchy principal value of the otherwise ill-defined expression : Similarly, we have : but : The former is the principal value of the otherwise ill-defined expression : All of the above limits are cases of theindeterminate form
In calculus and other branches of mathematical analysis, limits involving an algebraic combination of functions in an independent variable may often be evaluated by replacing these functions by their limits; if the expression obtained after this s ...
∞ − ∞.
These pathologies
Pathology is the study of the causes and effects of disease or injury. The word ''pathology'' also refers to the study of disease in general, incorporating a wide range of biology research fields and medical practices. However, when used in ...
do not affect "Lebesgue-integrable" functions, that is, functions the integrals of whose absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
s are finite.
Summability
An improper integral may diverge in the sense that the limit defining it may not exist. In this case, there are more sophisticated definitions of the limit which can produce a convergent value for the improper integral. These are calledsummability
In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a finite limit.
If a series converges, the individual terms of the series must ...
methods.
One summability method, popular in Fourier analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph ...
, is that of Cesàro summation
In mathematical analysis, Cesàro summation (also known as the Cesàro mean
) assigns values to some infinite sums that are not necessarily convergent in the usual sense. The Cesàro sum is defined as the limit, as ''n'' tends to infinity, of ...
. The integral
:
is Cesàro summable (C, α) if
:
exists and is finite . The value of this limit, should it exist, is the (C, α) sum of the integral.
An integral is (C, 0) summable precisely when it exists as an improper integral. However, there are integrals which are (C, α) summable for α > 0 which fail to converge as improper integrals (in the sense of Riemann or Lebesgue). One example is the integral
:
which fails to exist as an improper integral, but is (C,''α'') summable for every ''α'' > 0. This is an integral version of Grandi's series.
Multivariable improper integrals
The improper integral can also be defined for functions of several variables. The definition is slightly different, depending on whether one requires integrating over an unbounded domain, such as , or is integrating a function with singularities, like .Improper integrals over arbitrary domains
If is a non-negative function that is Riemann integrable over every compact cube of the form , for , then the improper integral of ''f'' over is defined to be the limit : provided it exists. A function on an arbitrary domain ''A'' in is extended to a function on by zero outside of ''A'': : The Riemann integral of a function over a bounded domain ''A'' is then defined as the integral of the extended function over a cube containing ''A'': : More generally, if ''A'' is unbounded, then the improper Riemann integral over an arbitrary domain in is defined as the limit: :Improper integrals with singularities
If ''f'' is a non-negative function which is unbounded in a domain ''A'', then the improper integral of ''f'' is defined by truncating ''f'' at some cutoff ''M'', integrating the resulting function, and then taking the limit as ''M'' tends to infinity. That is for , set . Then define : provided this limit exists.Functions with both positive and negative values
These definitions apply for functions that are non-negative. A more general function ''f'' can be decomposed as a difference of its positive part and negative part , so : with and both non-negative functions. The function ''f'' has an improper Riemann integral if each of and has one, in which case the value of that improper integral is defined by : In order to exist in this sense, the improper integral necessarily converges absolutely, since :: "The relevant notion here is that of unconditional convergence." ... "In fact, for improper integrals of such functions, unconditional convergence turns out to be equivalent to absolute convergence."Notes
Bibliography
* . * . * * . * *External links
Numerical Methods to Solve Improper Integrals
at Holistic Numerical Methods Institute {{integral Integral calculus