Hyperbolic Substitution

In mathematics, trigonometric substitution is the replacement of trigonometric functions for other expressions. In calculus, trigonometric substitution is a technique for evaluating integrals. Moreover, one may use the trigonometric identities to simplify certain integrals containing radical expressions. Like other methods of integration by substitution, when evaluating a definite integral, it may be simpler to completely deduce the antiderivative before applying the boundaries of integration.

Case I: Integrands containing ''a''² − ''x''²

Let $x = a \sin \theta$, and use the identity $1-\sin^2 \theta = \cos^2 \theta$.

Examples of Case I

Example 1

In the integral

:$\int\frac,$

we may use

:$x=a\sin \theta,\quad dx=a\cos\theta\, d\theta, \quad \theta=\arcsin\frac.$

Then,
:\begin
\int\frac &= \int\frac \\ pt &= \int\frac \\ pt &= \int\frac \\ pt &= \int d\theta \\ pt &= \theta + C \\ pt &= \arcsin\frac+C.
\end

The above step requires that $a > 0$ and $\cos \theta > 0$. We can choose $a$ to be the principal root of $a^2$, and impose the restriction $-\pi /2 < \theta < \pi /2$ by using the inverse sine function.

For a definite integral, one must figure out how the bounds of integration change. For example, as $x$ goes from $0$ to $a/2$, then $\sin \theta$ goes from $0$ to $1/2$, so $\theta$ goes from $0$ to $\pi / 6$. Then,

:$\int_0^\frac=\int_0^ d\theta = \frac.$

Some care is needed when picking the bounds. Because integration above requires that $-\pi /2 < \theta < \pi /2$ , $\theta$ can only go from $0$ to $\pi / 6$. Neglecting this restriction, one might have picked $\theta$ to go from $\pi$ to $5\pi /6$, which would have resulted in the negative of the actual value.

Alternatively, fully evaluate the indefinite integrals before applying the boundary conditions. In that case, the antiderivative gives

:$\int_^ \frac = \arcsin \left( \frac \right) \Biggl, _^ = \arcsin \left ( \frac\right) - \arcsin (0) = \frac$ as before.

Example 2

The integral

:$\int\sqrt\,dx,$

may be evaluated by letting $x=a\sin \theta,\, dx=a\cos\theta\, d\theta,\, \theta=\arcsin\frac,$

where $a > 0$ so that $\sqrt=a$, and $-\frac \le \theta \le \frac$ by the range of arcsine, so that $\cos \theta \ge 0$ and $\sqrt = \cos \theta$.

Then,
:\begin
\int\sqrt\,dx &= \int\sqrt\,(a\cos\theta) \,d\theta \\ pt &= \int\sqrt\,(a\cos\theta) \,d\theta \\ pt &= \int\sqrt\,(a\cos\theta) \,d\theta \\ pt &= \int(a\cos\theta)(a\cos\theta) \,d\theta \\ pt &= a^2\int\cos^2\theta\,d\theta \\ pt &= a^2\int\left(\frac\right)\,d\theta \\ pt &= \frac \left(\theta+\frac\sin 2\theta \right) + C \\ pt &= \frac(\theta+\sin\theta\cos\theta) + C \\ pt &= \frac\left(\arcsin\frac+\frac\sqrt\right) + C \\ pt &= \frac\arcsin\frac+\frac\sqrt+C.
\end

For a definite integral, the bounds change once the substitution is performed and are determined using the equation $\theta = \arcsin\frac$, with values in the range $-\frac \le \theta \le \frac$. Alternatively, apply the boundary terms directly to the formula for the antiderivative.

For example, the definite integral

:$\int_^1\sqrt\,dx,$

may be evaluated by substituting $x = 2\sin\theta, \,dx = 2\cos\theta\,d\theta$, with the bounds determined using $\theta = \arcsin\frac$.

Since $\arcsin(1/2) = \pi/6$ and $\arcsin(-1/2) = -\pi/6$,
:\begin
\int_^1\sqrt\,dx &= \int_^\sqrt\,(2\cos\theta) \,d\theta \\ pt &= \int_^\sqrt\,(2\cos\theta) \,d\theta \\ pt &= \int_^\sqrt\,(2\cos\theta) \,d\theta \\ pt &= \int_^(2\cos\theta)(2\cos\theta) \,d\theta \\ pt &= 4\int_^\cos^2\theta\,d\theta \\ pt &= 4\int_^\left(\frac\right)\,d\theta \\ pt &= 2 \left theta+\frac \sin 2\theta \right_
= \theta+\sin 2\theta\Biggl , ^_ \\ pt &= \left(\frac+\sin\frac\right)-\left(-\frac+\sin\left(-\frac\right)\right)
= \frac+\sqrt.
\end

On the other hand, direct application of the boundary terms to the previously obtained formula for the antiderivative yields
:\begin
\int_^1\sqrt\,dx &= \left \frac\arcsin\frac+\frac\sqrt \right^\\ pt&= \left( 2 \arcsin \frac + \frac\sqrt\right) - \left( 2 \arcsin \left(-\frac\right) + \frac\sqrt\right)\\ pt&= \left( 2 \cdot \frac + \frac\right) - \left( 2\cdot \left(-\frac\right) - \frac\right)\\ pt&= \frac + \sqrt
\end
as before.

Case II: Integrands containing ''a''² + ''x''²

Let $x = a \tan \theta$, and use the identity $1+\tan^2 \theta = \sec^2 \theta$.

Examples of Case II

Example 1

In the integral

:$\int\frac$

we may write

:$x=a\tan\theta,\quad dx=a\sec^2\theta\, d\theta, \quad \theta=\arctan\frac,$

so that the integral becomes

:\begin
\int\frac &= \int\frac \\ pt &= \int\frac \\ pt &= \int\frac \\ pt &= \int\frac \\ pt &= \frac+C \\ pt &= \frac \arctan \frac + C,
\end

provided $a \neq 0$.

For a definite integral, the bounds change once the substitution is performed and are determined using the equation $\theta = \arctan\frac$, with values in the range $-\frac < \theta < \frac$. Alternatively, apply the boundary terms directly to the formula for the antiderivative.

For example, the definite integral

:$\int_0^1\frac\,$

may be evaluated by substituting $x = \tan\theta, \,dx = \sec^2\theta\,d\theta$, with the bounds determined using $\theta = \arctan x$.

Since $\arctan 0 = 0$ and $\arctan 1 = \pi/4$,
:\begin
\int_0^1\frac &= 4\int_0^1\frac \\ pt &= 4\int_0^\frac \\ pt &= 4\int_0^\frac \\ pt &= 4\int_0^d\theta \\ pt &= (4\theta)\Bigg, ^_0 = 4 \left (\frac - 0 \right) = \pi.
\end

Meanwhile, direct application of the boundary terms to the formula for the antiderivative yields
:\begin
\int_0^1\frac\,
&= 4\int_0^1\frac \\
&= 4\left frac \arctan \frac \right1_0 \\
&= 4(\arctan x)\Bigg, ^1_0 \\
&= 4(\arctan 1 - \arctan 0) \\
&= 4 \left (\frac - 0 \right) = \pi,
\end
same as before.

Example 2

The integral

:$\int\sqrt\,$

may be evaluated by letting $x=a\tan\theta,\, dx=a\sec^2\theta\, d\theta, \, \theta=\arctan\frac,$

where $a > 0$ so that $\sqrt=a$, and $-\frac<\theta<\frac$ by the range of arctangent, so that $\sec \theta > 0$ and $\sqrt = \sec \theta$.

Then,
:\begin
\int\sqrt\,dx &= \int\sqrt\,(a \sec^2\theta)\, d\theta \\ pt &= \int\sqrt\,(a \sec^2\theta)\, d\theta \\ pt &= \int\sqrt\,(a \sec^2\theta)\, d\theta \\ pt &= \int(a \sec\theta)(a \sec^2\theta)\, d\theta \\ pt &= a^2\int \sec^3\theta\, d\theta. \\ pt \end
The integral of secant cubed may be evaluated using integration by parts. As a result,
:\begin
\int\sqrt\,dx &= \frac(\sec\theta \tan\theta + \ln, \sec\theta+\tan\theta, )+C \\ pt &= \frac\left(\sqrt\cdot\frac + \ln\left, \sqrt+\frac\\right)+C \\ pt &= \frac\left(x\sqrt + a^2\ln\left, \frac\\right)+C.
\end

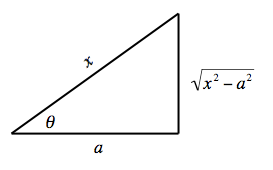
Case III: Integrands containing ''x''² − ''a''²

Let $x = a \sec \theta$, and use the identity $\sec^2 \theta -1 = \tan^2 \theta.$

Examples of Case III

Integrals like

:$\int\frac$

can also be evaluated by partial fractions rather than trigonometric substitutions. However, the integral

:$\int\sqrt\, dx$

cannot. In this case, an appropriate substitution is:
:$x = a \sec\theta,\, dx = a \sec\theta\tan\theta\, d\theta, \, \theta = \arcsec\frac,$

where $a > 0$ so that $\sqrt=a$, and $0 \le \theta < \frac$ by assuming $x > 0$, so that $\tan \theta \ge 0$ and $\sqrt = \tan \theta$.

Then,
:$\begin \int\sqrt\, dx &= \int\sqrt \cdot a \sec\theta\tan\theta\, d\theta \\ &= \int\sqrt \cdot a \sec\theta\tan\theta\, d\theta \\ &= \int\sqrt \cdot a \sec\theta\tan\theta\, d\theta \\ &= \int a^2 \sec\theta\tan^2\theta\, d\theta \\ &= a^2 \int (\sec\theta)(\sec^2\theta - 1)\, d\theta \\ &= a^2 \int (\sec^3\theta - \sec\theta)\, d\theta. \end$

One may evaluate the integral of the secant function by multiplying the numerator and denominator by $( \sec \theta + \tan \theta)$ and the integral of secant cubed by parts. As a result,
:\begin
\int\sqrt\,dx &= \frac(\sec\theta \tan\theta + \ln, \sec\theta+\tan\theta, )-a^2\ln, \sec\theta+\tan\theta, +C \\ pt &= \frac(\sec\theta \tan\theta - \ln, \sec\theta+\tan\theta, )+C \\ pt &= \frac\left(\frac\cdot\sqrt - \ln\left, \frac+\sqrt\\right)+C \\ pt &= \frac\left(x\sqrt - a^2\ln\left, \frac\\right)+C.
\end

When $\frac < \theta \le \pi$, which happens when $x < 0$ given the range of arcsecant, $\tan \theta \le 0$, meaning $\sqrt = -\tan \theta$ instead in that case.

Substitutions that eliminate trigonometric functions

Substitution can be used to remove trigonometric functions.

For instance,

:\begin
\int f(\sin(x), \cos(x))\, dx &=\int\frac1 f\left(u,\pm\sqrt\right)\, du && u=\sin (x) \\ pt\int f(\sin(x), \cos(x))\, dx &=\int\frac f\left(\pm\sqrt,u\right)\, du && u=\cos (x) \\ pt\int f(\sin(x), \cos(x))\, dx &=\int\frac2 f \left(\frac,\frac\right)\, du && u=\tan\left (\tfrac \right ) \\ pt\end

The last substitution is known as the Weierstrass substitution, which makes use of tangent half-angle formulas.

For example,

:$\begin \int\frac\, dx &= \int\frac2\frac\, du = \int (1-u^2)(1+u^2)\, du \\&= \int (1-u^4)\,du = u - \frac + C = \tan \frac - \frac \tan^5 \frac + C. \end$

Hyperbolic substitution

Substitutions of hyperbolic functions can also be used to simplify integrals.

In the integral $\int \frac\,$, make the substitution $x=a\sinh$, $dx=a\cosh u\, du.$

Then, using the identities $\cosh^2 (x) - \sinh^2 (x) = 1$ and $\sinh^ = \ln(x + \sqrt),$

\begin
\int \frac\, &= \int \frac\ , \\ pt&=\int \frac\, \\ pt&=\int \frac\, du\\ pt&=u+C\\ pt&=\sinh^+C\\ pt&=\ln\left(\sqrt + \frac\right) + C\\ pt&=\ln\left(\frac\right) + C
\end

See also

* Integration by substitution
* Weierstrass substitution
* Euler substitution

References

{{Integrals
Integral calculus
Trigonometry