|
Integral Of The Secant Function
In calculus, the integral of the secant function can be evaluated using a variety of methods and there are multiple ways of expressing the antiderivative, all of which can be shown to be equivalent via trigonometric identities, : \int \sec \theta \, d\theta = \begin \dfrac12 \ln \left, \dfrac\ + C \\ 5pt\ln\left, \sec\theta + \tan\theta\ + C \\ 5pt\ln\left, \tan\left(\dfrac + \dfrac\right) \ + C\\ 5pt\end This formula is useful for evaluating various trigonometric integrals. In particular, it can be used to evaluate the integral of the secant cubed, which, though seemingly special, comes up rather frequently in applications. Proof that the different antiderivatives are equivalent Trigonometric forms : \int \sec \theta \, d\theta = \left\\text The second of these follows by first multiplying top and bottom of the interior fraction by . This gives in the denominator, and the result follows by moving the factor of into the logarithm as a square root. Leaving out the cons ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involving certain functions of one or more angles. They are distinct from triangle identities, which are identities potentially involving angles but also involving side lengths or other lengths of a triangle. These identities are useful whenever expressions involving trigonometric functions need to be simplified. An important application is the integration of non-trigonometric functions: a common technique involves first using the substitution rule with a trigonometric function, and then simplifying the resulting integral with a trigonometric identity. Pythagorean identities The basic relationship between the sine and cosine is given by the Pythagorean identity: :\sin^2\theta + \cos^2\theta = 1, where \sin^2 \theta means (\sin \theta)^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a " natural philosopher"), widely recognised as one of the greatest mathematicians and physicists and among the most influential scientists of all time. He was a key figure in the philosophical revolution known as the Enlightenment. His book (''Mathematical Principles of Natural Philosophy''), first published in 1687, established classical mechanics. Newton also made seminal contributions to optics, and shares credit with German mathematician Gottfried Wilhelm Leibniz for developing infinitesimal calculus. In the , Newton formulated the laws of motion and universal gravitation that formed the dominant scientific viewpoint for centuries until it was superseded by the theory of relativity. Newton used his mathematical description of gravity to derive Kepler's laws of planetary motion, account for ti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complex Exponential
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, although it can be extended to the complex numbers or generalized to other mathematical objects like matrices or Lie algebras. The exponential function originated from the notion of exponentiation (repeated multiplication), but modern definitions (there are several equivalent characterizations) allow it to be rigorously extended to all real arguments, including irrational numbers. Its ubiquitous occurrence in pure and applied mathematics led mathematician Walter Rudin to opine that the exponential function is "the most important function in mathematics". The exponential function satisfies the exponentiation identity e^ = e^x e^y \text x,y\in\mathbb, which, along with the definition e = \exp(1), shows that e^n=\underbrace_ for positive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Function
In mathematics, the sign function or signum function (from '' signum'', Latin for "sign") is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as . To avoid confusion with the sine function, this function is usually called the signum function. Definition The signum function of a real number is a piecewise function which is defined as follows: \sgn x :=\begin -1 & \text x 0. \end Properties Any real number can be expressed as the product of its absolute value and its sign function: x = , x, \sgn x. It follows that whenever is not equal to 0 we have \sgn x = \frac = \frac\,. Similarly, for ''any'' real number , , x, = x\sgn x. We can also ascertain that: \sgn x^n=(\sgn x)^n. The signum function is the derivative of the absolute value function, up to (but not including) the indeterminacy at zero. More formally, in integration theory it is a weak derivative, and in convex functio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Cosecant
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. 328 from which are derived: * hyperbolic tangent "" (), * hyp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Secant
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions occur in the calculations of angles and distances in hyperbolic geometry. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, fluid dynamics, and special relativity. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictionary'', p. 328 from which are derived: * hyperbolic tangent "" (), * hyperb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosecant
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
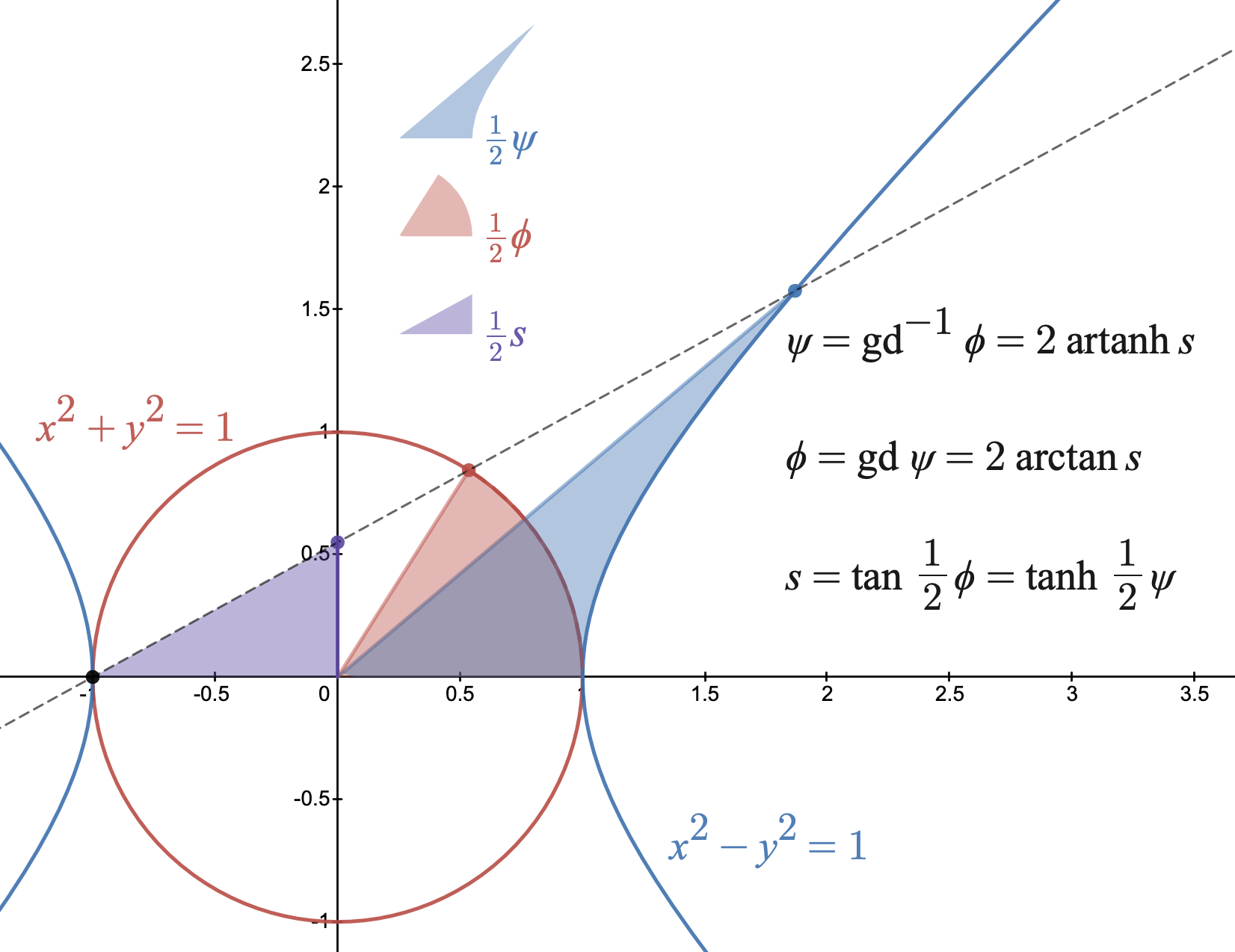
Tangent Half-angle Substitution
In integral calculus, the tangent half-angle substitution is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of x into an ordinary rational function of t by setting t = \tan \tfrac x2. This is the one-dimensional stereographic projection of the unit circle parametrized by angle measure onto the real line. The general transformation formula is: \int f(\sin x, \cos x)\, dx =\int f \frac. The tangent of half an angle is important in spherical trigonometry and was sometimes known in the 17th century as the half tangent or semi-tangent. Leonhard Euler used it to evaluate the integral \int dx / (a + b\cos x) in his 1768 integral calculus textbook, and Adrien-Marie Legendre described the general method in 1817. The substitution is described in most integral calculus textbooks since the late 19th century, usually without any special name. It is known in Russia as the universal trigonometric substitution, and also known ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Fraction
In algebra, the partial fraction decomposition or partial fraction expansion of a rational fraction (that is, a fraction such that the numerator and the denominator are both polynomials) is an operation that consists of expressing the fraction as a sum of a polynomial (possibly zero) and one or several fractions with a simpler denominator. The importance of the partial fraction decomposition lies in the fact that it provides algorithms for various computations with rational functions, including the explicit computation of antiderivatives, Taylor series expansions, inverse Z-transforms, and inverse Laplace transforms. The concept was discovered independently in 1702 by both Johann Bernoulli and Gottfried Leibniz. In symbols, the ''partial fraction decomposition'' of a rational fraction of the form \frac, where and are polynomials, is its expression as \frac=p(x) + \sum_j \frac where is a polynomial, and, for each , the denominator is a power of an irreducible p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isaac Barrow
Isaac Barrow (October 1630 – 4 May 1677) was an English Christian theologian and mathematician who is generally given credit for his early role in the development of infinitesimal calculus; in particular, for proof of the fundamental theorem of calculus. His work centered on the properties of the tangent; Barrow was the first to calculate the tangents of the kappa curve. He is also notable for being the inaugural holder of the prestigious Lucasian Professorship of Mathematics, a post later held by his student, Isaac Newton. Life Early life and education Barrow was born in London. He was the son of Thomas Barrow, a linen draper by trade. In 1624, Thomas married Ann, daughter of William Buggin of North Cray, Kent and their son Isaac was born in 1630. It appears that Barrow was the only child of this union—certainly the only child to survive infancy. Ann died around 1634, and the widowed father sent the lad to his grandfather, Isaac, the Cambridgeshire J.P., who resided ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartography
Cartography (; from grc, χάρτης , "papyrus, sheet of paper, map"; and , "write") is the study and practice of making and using maps. Combining science, aesthetics and technique, cartography builds on the premise that reality (or an imagined reality) can be modeled in ways that communicate spatial information effectively. The fundamental objectives of traditional cartography are to: * Set the map's agenda and select traits of the object to be mapped. This is the concern of map editing. Traits may be physical, such as roads or land masses, or may be abstract, such as toponyms or political boundaries. * Represent the terrain of the mapped object on flat media. This is the concern of map projections. * Eliminate characteristics of the mapped object that are not relevant to the map's purpose. This is the concern of generalization. * Reduce the complexity of the characteristics that will be mapped. This is also the concern of generalization. * Orchestrate the elements of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integral Of Secant Cubed
The integral of secant cubed is a frequent and challenging indefinite integral of elementary calculus: :\begin \int \sec^3 x \, dx &= \tfrac12\sec x \tan x + \tfrac12 \int \sec x\, dx + C \\ mu&= \tfrac12(\sec x \tan x + \ln \left, \sec x + \tan x\) + C \\ mu&= \tfrac12(\sec x \tan x + \operatorname^ x) + C, \qquad , x, < \tfrac12\pi \end where is the inverse , the . There are a number of reasons why this particular antiderivative is worthy of special attention: * The technique used for reducing integrals of higher odd powers of secant to lower ones is fully present in this, the simp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |