algebra on:
[Wikipedia]
[Google]
[Amazon]
Algebra is a branch of
 Systems of equations can be interpreted as geometric figures. For systems with two variables, each equation represents a line in two-dimensional space. The point where the two lines intersect is the solution of the full system because this is the only point that solves both the first and the second equation. For inconsistent systems, the two lines run parallel, meaning that there is no solution since they never intersect. If two equations are not independent then they describe the same line, meaning that every solution of one equation is also a solution of the other equation. These relations make it possible to seek solutions graphically by plotting the equations and determining where they intersect. The same principles also apply to systems of equations with more variables, with the difference being that the equations do not describe lines but higher dimensional figures. For instance, equations with three variables correspond to planes in three-dimensional space, and the points where all planes intersect solve the system of equations.
Systems of equations can be interpreted as geometric figures. For systems with two variables, each equation represents a line in two-dimensional space. The point where the two lines intersect is the solution of the full system because this is the only point that solves both the first and the second equation. For inconsistent systems, the two lines run parallel, meaning that there is no solution since they never intersect. If two equations are not independent then they describe the same line, meaning that every solution of one equation is also a solution of the other equation. These relations make it possible to seek solutions graphically by plotting the equations and determining where they intersect. The same principles also apply to systems of equations with more variables, with the difference being that the equations do not describe lines but higher dimensional figures. For instance, equations with three variables correspond to planes in three-dimensional space, and the points where all planes intersect solve the system of equations.
 On a formal level, an algebraic structure is a set of mathematical objects, called the underlying set, together with one or several operations. Abstract algebra is primarily interested in
On a formal level, an algebraic structure is a set of mathematical objects, called the underlying set, together with one or several operations. Abstract algebra is primarily interested in
 Besides groups, rings, and fields, there are many other algebraic structures studied by algebra. They include magmas, semigroups, monoids, abelian groups,
Besides groups, rings, and fields, there are many other algebraic structures studied by algebra. They include magmas, semigroups, monoids, abelian groups,  Another tool of comparison is the relation between an algebraic structure and its subalgebra. The algebraic structure and its subalgebra use the same operations, which follow the same axioms. The only difference is that the underlying set of the subalgebra is a subset of the underlying set of the algebraic structure. All operations in the subalgebra are required to be closed in its underlying set, meaning that they only produce elements that belong to this set. For example, the set of even integers together with addition is a subalgebra of the full set of integers together with addition. This is the case because the sum of two even numbers is again an even number. But the set of odd integers together with addition is not a subalgebra because it is not closed: adding two odd numbers produces an even number, which is not part of the chosen subset.
Universal algebra is the study of algebraic structures in general. As part of its general perspective, it is not concerned with the specific elements that make up the underlying sets and considers operations with more than two inputs, such as ternary operations. It provides a framework for investigating what structural features different algebraic structures have in common. One of those structural features concerns the identities that are true in different algebraic structures. In this context, an identity is a universal equation or an equation that is true for all elements of the underlying set. For example, commutativity is a universal equation that states that is identical to for all elements. A variety is a class of all algebraic structures that satisfy certain identities. For example, if two algebraic structures satisfy commutativity then they are both part of the corresponding variety.
Another tool of comparison is the relation between an algebraic structure and its subalgebra. The algebraic structure and its subalgebra use the same operations, which follow the same axioms. The only difference is that the underlying set of the subalgebra is a subset of the underlying set of the algebraic structure. All operations in the subalgebra are required to be closed in its underlying set, meaning that they only produce elements that belong to this set. For example, the set of even integers together with addition is a subalgebra of the full set of integers together with addition. This is the case because the sum of two even numbers is again an even number. But the set of odd integers together with addition is not a subalgebra because it is not closed: adding two odd numbers produces an even number, which is not part of the chosen subset.
Universal algebra is the study of algebraic structures in general. As part of its general perspective, it is not concerned with the specific elements that make up the underlying sets and considers operations with more than two inputs, such as ternary operations. It provides a framework for investigating what structural features different algebraic structures have in common. One of those structural features concerns the identities that are true in different algebraic structures. In this context, an identity is a universal equation or an equation that is true for all elements of the underlying set. For example, commutativity is a universal equation that states that is identical to for all elements. A variety is a class of all algebraic structures that satisfy certain identities. For example, if two algebraic structures satisfy commutativity then they are both part of the corresponding variety.
 The origin of algebra lies in attempts to solve mathematical problems involving arithmetic calculations and unknown quantities. These developments happened in the ancient period in
The origin of algebra lies in attempts to solve mathematical problems involving arithmetic calculations and unknown quantities. These developments happened in the ancient period in  Starting in the mid-19th century, interest in algebra shifted from the study of polynomials associated with elementary algebra towards a more general inquiry into algebraic structures, marking the emergence of
Starting in the mid-19th century, interest in algebra shifted from the study of polynomials associated with elementary algebra towards a more general inquiry into algebraic structures, marking the emergence of
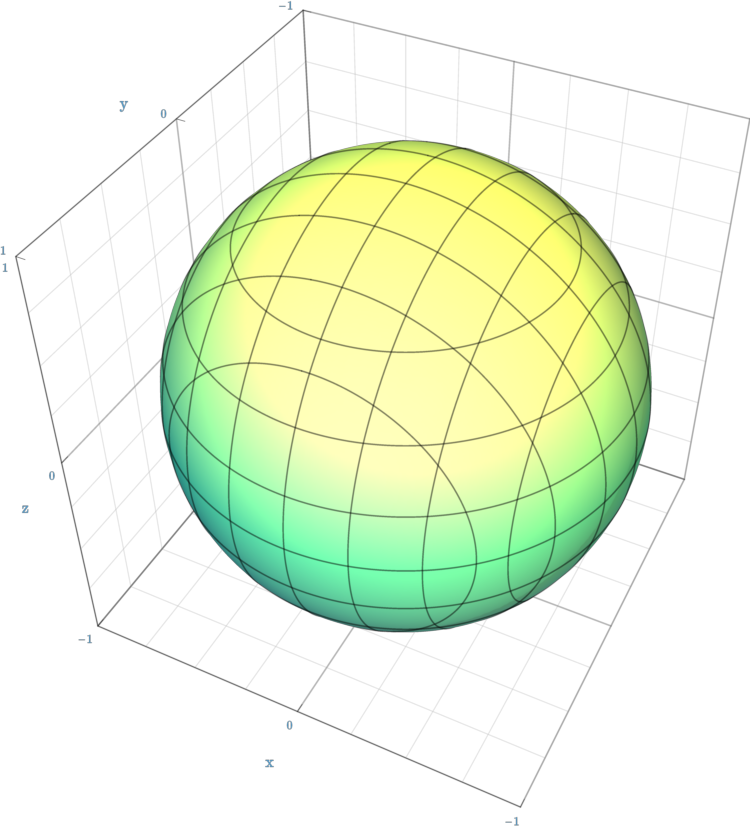 One application, found in geometry, is the use of algebraic statements to describe geometric figures. For example, the equation describes a line in two-dimensional space while the equation corresponds to a
One application, found in geometry, is the use of algebraic statements to describe geometric figures. For example, the equation describes a line in two-dimensional space while the equation corresponds to a
 Algebra education mostly focuses on elementary algebra, which is one of the reasons why elementary algebra is also called school algebra. It is usually not introduced until
Algebra education mostly focuses on elementary algebra, which is one of the reasons why elementary algebra is also called school algebra. It is usually not introduced until
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
that deals with abstract system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
s, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations, such as addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
and multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
.
Elementary algebra is the main form of algebra taught in schools. It examines mathematical statements using variables for unspecified values and seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equation
In mathematics, a linear equation is an equation that may be put in the form
a_1x_1+\ldots+a_nx_n+b=0, where x_1,\ldots,x_n are the variables (or unknowns), and b,a_1,\ldots,a_n are the coefficients, which are often real numbers. The coeffici ...
s and combinations of them called '' systems of linear equations''. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions.
Abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures, which are set (mathematics), sets with specific operation (mathematics), operations acting on their elements. Algebraic structur ...
studies algebraic structures, which consist of a set of mathematical objects together with one or several operations defined on that set. It is a generalization of elementary and linear algebra since it allows mathematical objects other than numbers and non-arithmetic operations. It distinguishes between different types of algebraic structures, such as groups, rings, and fields, based on the number of operations they use and the laws they follow, called axioms. Universal algebra and category theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory ...
provide general frameworks to investigate abstract patterns that characterize different classes of algebraic structures.
Algebraic methods were first studied in the ancient period to solve specific problems in fields like geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
. Subsequent mathematicians examined general techniques to solve equations independent of their specific applications. They described equations and their solutions using words and abbreviations until the 16th and 17th centuries when a rigorous symbolic formalism was developed. In the mid-19th century, the scope of algebra broadened beyond a theory of equations to cover diverse types of algebraic operations and structures. Algebra is relevant to many branches of mathematics, such as geometry, topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
, and calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
, and other fields of inquiry, like logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure o ...
and the empirical sciences.
Definition and etymology
Algebra is the branch of mathematics that studies algebraic structures and the operations they use. An algebraic structure is a non-empty set of mathematical objects, such as theinteger
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
s, together with algebraic operations defined on that set, like addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
and multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
. Algebra explores the laws, general characteristics, and types of algebraic structures. Within certain algebraic structures, it examines the use of variables in equations and how to manipulate these equations.
Algebra is often understood as a generalization of arithmetic. Arithmetic studies operations like addition, subtraction, multiplication, and division, in a particular domain of numbers, such as the real numbers. Elementary algebra constitutes the first level of abstraction. Like arithmetic, it restricts itself to specific types of numbers and operations. It generalizes these operations by allowing indefinite quantities in the form of variables in addition to numbers. A higher level of abstraction is found in abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures, which are set (mathematics), sets with specific operation (mathematics), operations acting on their elements. Algebraic structur ...
, which is not limited to a particular domain and examines algebraic structures such as groups and rings. It extends beyond typical arithmetic operations by also covering other types of operations. Universal algebra is still more abstract in that it is not interested in specific algebraic structures but investigates the characteristics of algebraic structures in general.
The term "algebra" is sometimes used in a more narrow sense to refer only to elementary algebra or only to abstract algebra. When used as a countable noun, an algebra is a specific type of algebraic structure that involves a vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
equipped with a certain type of binary operation. Depending on the context, "algebra" can also refer to other algebraic structures, like a Lie algebra
In mathematics, a Lie algebra (pronounced ) is a vector space \mathfrak g together with an operation called the Lie bracket, an alternating bilinear map \mathfrak g \times \mathfrak g \rightarrow \mathfrak g, that satisfies the Jacobi ident ...
or an associative algebra.
The word ''algebra'' comes from the Arabic
Arabic (, , or , ) is a Central Semitic languages, Central Semitic language of the Afroasiatic languages, Afroasiatic language family spoken primarily in the Arab world. The International Organization for Standardization (ISO) assigns lang ...
term (), which originally referred to the surgical treatment of bonesetting. In the 9th century, the term received a mathematical meaning when the Persian mathematician Muhammad ibn Musa al-Khwarizmi employed it to describe a method of solving equations and used it in the title of a treatise on algebra, 'The Compendious Book on Calculation by Completion and Balancing''which was translated into Latin as . The word entered the English language in the 16th century from Italian, Spanish, and medieval Latin
Latin ( or ) is a classical language belonging to the Italic languages, Italic branch of the Indo-European languages. Latin was originally spoken by the Latins (Italic tribe), Latins in Latium (now known as Lazio), the lower Tiber area aroun ...
. Initially, its meaning was restricted to the theory of equations, that is, to the art of manipulating polynomial equations in view of solving them. This changed in the 19th century when the scope of algebra broadened to cover the study of diverse types of algebraic operations and structures together with their underlying axioms, the laws they follow.
Major branches
Elementary algebra
Elementary algebra, also called school algebra, college algebra, and classical algebra, is the oldest and most basic form of algebra. It is a generalization of arithmetic that relies on variables and examines how mathematical statements may be transformed. Arithmetic is the study of numerical operations and investigates how numbers are combined and transformed using the arithmetic operations ofaddition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
, subtraction, multiplication
Multiplication is one of the four elementary mathematical operations of arithmetic, with the other ones being addition, subtraction, and division (mathematics), division. The result of a multiplication operation is called a ''Product (mathem ...
, division, exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
, extraction of roots
A root is the part of a plant, generally underground, that anchors the plant body, and absorbs and stores water and nutrients.
Root or roots may also refer to:
Art, entertainment, and media
* ''The Root'' (magazine), an online magazine focusin ...
, and logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , the ...
. For example, the operation of addition combines two numbers, called the addends, into a third number, called the sum, as in
Elementary algebra relies on the same operations while allowing variables in addition to regular numbers. Variables are symbol
A symbol is a mark, Sign (semiotics), sign, or word that indicates, signifies, or is understood as representing an idea, physical object, object, or wikt:relationship, relationship. Symbols allow people to go beyond what is known or seen by cr ...
s for unspecified or unknown quantities. They make it possible to state relationships for which one does not know the exact values and to express general laws that are true, independent of which numbers are used. For example, the equation
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for ...
belongs to arithmetic and expresses an equality only for these specific numbers. By replacing the numbers with variables, it is possible to express a general law that applies to any possible combination of numbers, like the commutative property of multiplication, which is expressed in the equation
Algebraic expressions are formed by using arithmetic operations to combine variables and numbers. By convention, the lowercase letters , , and represent variables. In some cases, subscripts are added to distinguish variables, as in , , and . The lowercase letters , , and are usually used for constants and coefficients. The expression is an algebraic expression created by multiplying the number 5 with the variable and adding the number 3 to the result. Other examples of algebraic expressions are and
Some algebraic expressions take the form of statements that relate two expressions to one another. An equation is a statement formed by comparing two expressions, saying that they are equal. This can be expressed using the equals sign
The equals sign (British English) or equal sign (American English), also known as the equality sign, is the mathematical symbol , which is used to indicate equality. In an equation it is placed between two expressions that have the same valu ...
(), as in . Inequations involve a different type of comparison, saying that the two sides are different. This can be expressed using symbols such as the less-than sign
The less-than sign is a mathematical symbol that denotes an inequality between two values. The widely adopted form of two equal-length strokes connecting in an acute angle at the left, , has been found in documents dated as far back as the 1560 ...
(), the greater-than sign
The greater-than sign is a mathematical symbol that denotes an inequality between two values. The widely adopted form of two equal-length strokes connecting in an acute angle at the right, , has been found in documents dated as far back as 1631 ...
(), and the inequality sign (). Unlike other expressions, statements can be true or false, and their truth value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth, which in classical logic has only two possible values ('' true'' or '' false''). Truth values are used in ...
usually depends on the values of the variables. For example, the statement is true if is either 2 or −2 and false otherwise. Equations with variables can be divided into identity equations and conditional equations. Identity equations are true for all values that can be assigned to the variables, such as the equation . Conditional equations are only true for some values. For example, the equation is only true if is 5.
The main goal of elementary algebra is to determine the values for which a statement is true. This can be achieved by transforming and manipulating statements according to certain rules. A key principle guiding this process is that whatever operation is applied to one side of an equation also needs to be done to the other side. For example, if one subtracts 5 from the left side of an equation one also needs to subtract 5 from the right side to balance both sides. The goal of these steps is usually to isolate the variable one is interested in on one side, a process known as solving the equation for that variable. For example, the equation can be solved for by adding 7 to both sides, which isolates on the left side and results in the equation .
There are many other techniques used to solve equations. Simplification is employed to replace a complicated expression with an equivalent simpler one. For example, the expression can be replaced with the expression since by the distributive property. For statements with several variables, substitution is a common technique to replace one variable with an equivalent expression that does not use this variable. For example, if one knows that then one can simplify the expression to arrive at . In a similar way, if one knows the value of one variable one may be able to use it to determine the value of other variables.
Algebraic equations can be interpreted geometrically to describe spatial figures in the form of a graph. To do so, the different variables in the equation are understood as coordinates and the values that solve the equation are interpreted as points of a graph. For example, if is set to zero in the equation , then must be −1 for the equation to be true. This means that the -pair is part of the graph of the equation. The -pair , by contrast, does not solve the equation and is therefore not part of the graph. The graph encompasses the totality of -pairs that solve the equation.
Polynomials
A polynomial is an expression consisting of one or more terms that are added or subtracted from each other, like . Each term is either a constant, a variable, or a product of a constant and variables. Each variable can be raised to a positive integer power. A monomial is a polynomial with one term while two- and three-term polynomials are called binomials and trinomials. The degree of a polynomial is the maximal value (among its terms) of the sum of the exponents of the variables (4 in the above example). Polynomials of degree one are called ''linear polynomials''. Linear algebra studies systems of linear polynomials. A polynomial is said to be ''univariate'' or ''multivariate'', depending on whether it uses one or more variables. Factorization is a method used to simplify polynomials, making it easier to analyze them and determine the values for which they evaluate to zero. Factorization consists of rewriting a polynomial as a product of several factors. For example, the polynomial can be factorized as . The polynomial as a whole is zero if and only if one of its factors is zero, i.e., if is either −2 or 5. Before the 19th century, much of algebra was devoted to polynomial equations, that isequation
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for ...
s obtained by equating a polynomial to zero. The first attempts for solving polynomial equations were to express the solutions in terms of th roots. The solution of a second-degree polynomial equation of the form is given by the quadratic formula
Solutions for the degrees 3 and 4 are given by the cubic and quartic formulas. There are no general solutions for higher degrees, as proven in the 19th century by the Abel–Ruffini theorem. Even when general solutions do not exist, approximate solutions can be found by numerical tools like the Newton–Raphson method.
The fundamental theorem of algebra asserts that every univariate polynomial equation of positive degree with real or complex coefficients has at least one complex solution. Consequently, every polynomial of a positive degree can be factorized into linear polynomials. This theorem was proved at the beginning of the 19th century, but this does not close the problem since the theorem does not provide any way for computing the solutions.
Linear algebra
Linear algebra starts with the study of systems of linear equations. An equation is linear if it can be expressed in the form , where , , ..., and are constants. Examples are and . A ''system of linear equations'' is a set of linear equations for which one is interested in common solutions. Matrices are rectangular arrays of values that have been originally introduced for having a compact and synthetic notation for systems of linear equations. For example, the system of equations can be written as where , and are the matrices Under some conditions on the number of rows and columns, matrices can be added, multiplied, and sometimes inverted. All methods for solving linear systems may be expressed as matrix manipulations using these operations. For example, solving the above system consists of computing an inverted matrix such that where is the identity matrix. Then, multiplying on the left both members of the above matrix equation by one gets the solution of the system of linear equations as Methods of solving systems of linear equations range from the introductory, like substitution and elimination, to more advanced techniques using matrices, such as Cramer's rule, the Gaussian elimination, and LU decomposition. Some systems of equations are inconsistent, meaning that no solutions exist because the equations contradict each other. Consistent systems have either one unique solution or an infinite number of solutions. The study ofvector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
s and linear map
In mathematics, and more specifically in linear algebra, a linear map (also called a linear mapping, linear transformation, vector space homomorphism, or in some contexts linear function) is a mapping V \to W between two vector spaces that p ...
s form a large part of linear algebra. A vector space is an algebraic structure formed by a set with an addition that makes it an abelian group and a scalar multiplication that is compatible with addition (see vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
for details). A linear map is a function between vector spaces that is compatible with addition and scalar multiplication. In the case of finite-dimensional vector spaces, vectors and linear maps can be represented by matrices. It follows that the theories of matrices and finite-dimensional vector spaces are essentially the same. In particular, vector spaces provide a third way for expressing and manipulating systems of linear equations. From this perspective, a matrix is a representation of a linear map: if one chooses a particular basis to describe the vectors being transformed, then the entries in the matrix give the results of applying the linear map to the basis vectors.
Abstract algebra
Abstract algebra, also called modern algebra, is the study of algebraic structures. An algebraic structure is a framework for understanding operations on mathematical objects, like the addition of numbers. While elementary algebra and linear algebra work within the confines of particular algebraic structures, abstract algebra takes a more general approach that compares how algebraic structures differ from each other and what types of algebraic structures there are, such as groups, rings, and fields. The key difference between these types of algebraic structures lies in the number of operations they use and the laws they obey. Inmathematics education
In contemporary education, mathematics education—known in Europe as the didactics or pedagogy of mathematics—is the practice of teaching, learning, and carrying out Scholarly method, scholarly research into the transfer of mathematical know ...
, abstract algebra refers to an advanced undergraduate course that mathematics majors take after completing courses in linear algebra.
binary operation
In mathematics, a binary operation or dyadic operation is a rule for combining two elements (called operands) to produce another element. More formally, a binary operation is an operation of arity two.
More specifically, a binary operation ...
s, which take any two objects from the underlying set as inputs and map them to another object from this set as output. For example, the algebraic structure has the natural numbers () as the underlying set and addition () as its binary operation. The underlying set can contain mathematical objects other than numbers, and the operations are not restricted to regular arithmetic operations. For instance, the underlying set of the symmetry group of a geometric object is made up of geometric transformations, such as rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
s, under which the object remains unchanged. Its binary operation is function composition, which takes two transformations as input and has the transformation resulting from applying the first transformation followed by the second as its output.
Group theory
Abstract algebra classifies algebraic structures based on the laws or axioms that its operations obey and the number of operations it uses. One of the most basic types is a group, which has one operation and requires that this operation is associative and has anidentity element
In mathematics, an identity element or neutral element of a binary operation is an element that leaves unchanged every element when the operation is applied. For example, 0 is an identity element of the addition of real numbers. This concept is use ...
and inverse elements. An operation is associative if the order of several applications does not matter, i.e., if is the same as for all elements. An operation has an identity element or a neutral element if one element ''e'' exists that does not change the value of any other element, i.e., if . An operation has inverse elements if for any element there exists a reciprocal element that undoes . If an element operates on its inverse then the result is the neutral element ''e'', expressed formally as . Every algebraic structure that fulfills these requirements is a group. For example, is a group formed by the set of integers
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
together with the operation of addition. The neutral element is 0 and the inverse element of any number is The natural numbers with addition, by contrast, do not form a group since they contain only positive integers and therefore lack inverse elements.
Group theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field ( ...
examines the nature of groups, with basic theorems such as the fundamental theorem of finite abelian groups and the Feit–Thompson theorem. The latter was a key early step in one of the most important mathematical achievements of the 20th century: the collaborative effort, taking up more than 10,000 journal pages and mostly published between 1960 and 2004, that culminated in a complete classification of finite simple groups.
Ring theory and field theory
A ring is an algebraic structure with two operations that work similarly to the addition and multiplication of numbers and are named and generally denoted similarly. A ring is a commutative group under addition: the addition of the ring is associative, commutative, and has an identity element and inverse elements. The multiplication is associative and distributive with respect to addition; that is, and Moreover, multiplication is associative and has anidentity element
In mathematics, an identity element or neutral element of a binary operation is an element that leaves unchanged every element when the operation is applied. For example, 0 is an identity element of the addition of real numbers. This concept is use ...
generally denoted as . Multiplication needs not to be commutative; if it is commutative, one has a commutative ring
In mathematics, a commutative ring is a Ring (mathematics), ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra. Complementarily, noncommutative algebra is the study of ring prope ...
. The ring of integers () is one of the simplest commutative rings.
A '' field'' is a commutative ring such that and each nonzero element has a multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a ra ...
. The ring of integers does not form a field because it lacks multiplicative inverses. For example, the multiplicative inverse of is , which is not an integer. The rational numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction (mathematics), fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for examp ...
, the real numbers
In mathematics, a real number is a number that can be used to measurement, measure a continuous variable, continuous one-dimensional quantity such as a time, duration or temperature. Here, ''continuous'' means that pairs of values can have arbi ...
, and the complex numbers each form a field with the operations of addition and multiplication.
Ring theory is the study of rings, exploring concepts such as subrings, quotient rings, polynomial rings, and ideals as well as theorems such as Hilbert's basis theorem
In mathematics Hilbert's basis theorem asserts that every ideal (ring theory), ideal of a polynomial ring over a field (mathematics), field has a finite generating set of an ideal, generating set (a finite ''basis'' in Hilbert's terminology).
In ...
. Field theory is concerned with fields, examining field extensions, algebraic closures, and finite fields. Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field (mathematics), field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems ...
explores the relation between field theory and group theory, relying on the fundamental theorem of Galois theory.
Theories of interrelations among structures
commutative ring
In mathematics, a commutative ring is a Ring (mathematics), ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra. Complementarily, noncommutative algebra is the study of ring prope ...
s, modules, lattices, vector space
In mathematics and physics, a vector space (also called a linear space) is a set (mathematics), set whose elements, often called vector (mathematics and physics), ''vectors'', can be added together and multiplied ("scaled") by numbers called sc ...
s, algebras over a field, and associative and non-associative algebras. They differ from each other regarding the types of objects they describe and the requirements that their operations fulfill. Many are related to each other in that a basic structure can be turned into a more specialized structure by adding constraints. For example, a magma becomes a semigroup if its operation is associative.
Homomorphisms are tools to examine structural features by comparing two algebraic structures. A homomorphism is a function from the underlying set of one algebraic structure to the underlying set of another algebraic structure that preserves certain structural characteristics. If the two algebraic structures use binary operations and have the form and then the function is a homomorphism if it fulfills the following requirement: . The existence of a homomorphism reveals that the operation in the second algebraic structure plays the same role as the operation does in the first algebraic structure. Isomorphisms are a special type of homomorphism that indicates a high degree of similarity between two algebraic structures. An isomorphism is a bijective homomorphism, meaning that it establishes a one-to-one relationship between the elements of the two algebraic structures. This implies that every element of the first algebraic structure is mapped to one unique element in the second structure without any unmapped elements in the second structure.
Category theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory ...
examines how mathematical objects are related to each other using the concept of categories. A category is a collection of objects together with a collection of morphisms or "arrows" between those objects. These two collections must satisfy certain conditions. For example, morphisms can be joined, or ''composed'': if there exists a morphism from object to object , and another morphism from object to object , then there must also exist one from object to object . Composition of morphisms is required to be associative, and there must be an "identity morphism" for every object. Categories are widely used in contemporary mathematics since they provide a unifying framework to describe and analyze many fundamental mathematical concepts. For example, sets can be described with the category of sets, and any group can be regarded as the morphisms of a category with just one object.
History
 The origin of algebra lies in attempts to solve mathematical problems involving arithmetic calculations and unknown quantities. These developments happened in the ancient period in
The origin of algebra lies in attempts to solve mathematical problems involving arithmetic calculations and unknown quantities. These developments happened in the ancient period in Babylonia
Babylonia (; , ) was an Ancient history, ancient Akkadian language, Akkadian-speaking state and cultural area based in the city of Babylon in central-southern Mesopotamia (present-day Iraq and parts of Kuwait, Syria and Iran). It emerged as a ...
, Egypt
Egypt ( , ), officially the Arab Republic of Egypt, is a country spanning the Northeast Africa, northeast corner of Africa and Western Asia, southwest corner of Asia via the Sinai Peninsula. It is bordered by the Mediterranean Sea to northe ...
, Greece
Greece, officially the Hellenic Republic, is a country in Southeast Europe. Located on the southern tip of the Balkan peninsula, it shares land borders with Albania to the northwest, North Macedonia and Bulgaria to the north, and Turkey to th ...
, China
China, officially the People's Republic of China (PRC), is a country in East Asia. With population of China, a population exceeding 1.4 billion, it is the list of countries by population (United Nations), second-most populous country after ...
, and India
India, officially the Republic of India, is a country in South Asia. It is the List of countries and dependencies by area, seventh-largest country by area; the List of countries by population (United Nations), most populous country since ...
. One of the earliest documents on algebraic problems is the Rhind Mathematical Papyrus from ancient Egypt, which was written around 1650 BCE. It discusses solutions to linear equations, as expressed in problems like "A quantity; its fourth is added to it. It becomes fifteen. What is the quantity?" Babylonian clay tablets from around the same time explain methods to solve linear and quadratic polynomial equations, such as the method of completing the square.
Many of these insights found their way to the ancient Greeks. Starting in the 6th century BCE, their main interest was geometry rather than algebra, but they employed algebraic methods to solve geometric problems. For example, they studied geometric figures while taking their lengths and areas as unknown quantities to be determined, as exemplified in Pythagoras' formulation of the difference of two squares method and later in Euclid's ''Elements''. In the 3rd century CE, Diophantus provided a detailed treatment of how to solve algebraic equations in a series of books called '' Arithmetica''. He was the first to experiment with symbolic notation to express polynomials. Diophantus's work influenced Arab development of algebra with many of his methods reflected in the concepts and techniques used in medieval Arabic algebra. In ancient China, '' The Nine Chapters on the Mathematical Art'', a book composed over the period spanning from the 10th century BCE to the 2nd century CE, explored various techniques for solving algebraic equations, including the use of matrix-like constructs.
There is no unanimity of opinion as to whether these early developments are part of algebra or only precursors. They offered solutions to algebraic problems but did not conceive them in an abstract and general manner, focusing instead on specific cases and applications. This changed with the Persian mathematician al-Khwarizmi, who published his '' The Compendious Book on Calculation by Completion and Balancing'' in 825 CE. It presents the first detailed treatment of general methods that can be used to manipulate linear and quadratic equations by "reducing" and "balancing" both sides. Other influential contributions to algebra came from the Arab mathematician Thābit ibn Qurra also in the 9th century and the Persian mathematician Omar Khayyam
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīshābūrī (18 May 1048 – 4 December 1131) (Persian language, Persian: غیاث الدین ابوالفتح عمر بن ابراهیم خیام نیشابورﻯ), commonly known as Omar ...
in the 11th and 12th centuries.
In India, Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
investigated how to solve quadratic equations and systems of equations with several variables in the 7th century CE. Among his innovations were the use of zero and negative numbers in algebraic equations. The Indian mathematicians Mahāvīra in the 9th century and Bhāskara II in the 12th century further refined Brahmagupta's methods and concepts. In 1247, the Chinese mathematician Qin Jiushao wrote the '' Mathematical Treatise in Nine Sections'', which includes an algorithm for the numerical evaluation of polynomials, including polynomials of higher degrees.
The Italian mathematician Fibonacci
Leonardo Bonacci ( – ), commonly known as Fibonacci, was an Italians, Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages".
The name he is commonly called, ''Fibonacci ...
brought al-Khwarizmi's ideas and techniques to Europe in books including his '' Liber Abaci''. In 1545, the Italian polymath Gerolamo Cardano published his book '' Ars Magna'', which covered many topics in algebra, discussed imaginary numbers, and was the first to present general methods for solving cubic and quartic equations. In the 16th and 17th centuries, the French mathematicians François Viète and René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
introduced letters and symbols to denote variables and operations, making it possible to express equations in an concise and abstract manner. Their predecessors had relied on verbal descriptions of problems and solutions. Some historians see this development as a key turning point in the history of algebra and consider what came before it as the prehistory of algebra because it lacked the abstract nature based on symbolic manipulation.
In the 17th and 18th centuries, many attempts were made to find general solutions to polynomials of degree five and higher. All of them failed. At the end of the 18th century, the German mathematician Carl Friedrich Gauss proved the fundamental theorem of algebra, which describes the existence of zeros of polynomials of any degree without providing a general solution. At the beginning of the 19th century, the Italian mathematician Paolo Ruffini and the Norwegian mathematician Niels Henrik Abel were able to show that no general solution exists for polynomials of degree five and higher. In response to and shortly after their findings, the French mathematician Évariste Galois developed what came later to be known as Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field (mathematics), field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems ...
, which offered a more in-depth analysis of the solutions of polynomials while also laying the foundation of group theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field ( ...
. Mathematicians soon realized the relevance of group theory to other fields and applied it to disciplines like geometry and number theory.
 Starting in the mid-19th century, interest in algebra shifted from the study of polynomials associated with elementary algebra towards a more general inquiry into algebraic structures, marking the emergence of
Starting in the mid-19th century, interest in algebra shifted from the study of polynomials associated with elementary algebra towards a more general inquiry into algebraic structures, marking the emergence of abstract algebra
In mathematics, more specifically algebra, abstract algebra or modern algebra is the study of algebraic structures, which are set (mathematics), sets with specific operation (mathematics), operations acting on their elements. Algebraic structur ...
. This approach explored the axiomatic basis of arbitrary algebraic operations. The invention of new algebraic systems based on different operations and elements accompanied this development, such as Boolean algebra, vector algebra, and matrix algebra. Influential early developments in abstract algebra were made by the German mathematicians David Hilbert, Ernst Steinitz, and Emmy Noether
Amalie Emmy Noether (23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She also proved Noether's theorem, Noether's first and Noether's second theorem, second theorems, which ...
as well as the Austrian mathematician Emil Artin. They researched different forms of algebraic structures and categorized them based on their underlying axioms into types, like groups, rings, and fields.
The idea of the even more general approach associated with universal algebra was conceived by the English mathematician Alfred North Whitehead in his 1898 book ''A Treatise on Universal Algebra''. Starting in the 1930s, the American mathematician Garrett Birkhoff
Garrett Birkhoff (January 19, 1911 – November 22, 1996) was an American mathematician. He is best known for his work in lattice theory.
The mathematician George Birkhoff (1884–1944) was his father.
Life
The son of the mathematician Ge ...
expanded these ideas and developed many of the foundational concepts of this field. The invention of universal algebra led to the emergence of various new areas focused on the algebraization of mathematicsthat is, the application of algebraic methods to other branches of mathematics. Topological algebra arose in the early 20th century, studying algebraic structures such as topological groups and Lie groups. In the 1940s and 50s, homological algebra
Homological algebra is the branch of mathematics that studies homology (mathematics), homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology (a precurs ...
emerged, employing algebraic techniques to study homology. Around the same time, category theory
Category theory is a general theory of mathematical structures and their relations. It was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Category theory ...
was developed and has since played a key role in the foundations of mathematics
Foundations of mathematics are the mathematical logic, logical and mathematics, mathematical framework that allows the development of mathematics without generating consistency, self-contradictory theories, and to have reliable concepts of theo ...
. Other developments were the formulation of model theory
In mathematical logic, model theory is the study of the relationship between theory (mathematical logic), formal theories (a collection of Sentence (mathematical logic), sentences in a formal language expressing statements about a Structure (mat ...
and the study of free algebras.
Applications
The influence of algebra is wide-reaching, both within mathematics and in its applications to other fields. The algebraization of mathematics is the process of applying algebraic methods and principles to other branches of mathematics, such asgeometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...
, and calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
. It happens by employing symbols in the form of variables to express mathematical insights on a more general level, allowing mathematicians to develop formal models describing how objects interact and relate to each other.
 One application, found in geometry, is the use of algebraic statements to describe geometric figures. For example, the equation describes a line in two-dimensional space while the equation corresponds to a
One application, found in geometry, is the use of algebraic statements to describe geometric figures. For example, the equation describes a line in two-dimensional space while the equation corresponds to a sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
in three-dimensional space. Of special interest to algebraic geometry
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometry, geometrical problems. Classically, it studies zero of a function, zeros of multivariate polynomials; th ...
are algebraic varieties, which are solutions to systems of polynomial equations that can be used to describe more complex geometric figures. Algebraic reasoning can also solve geometric problems. For example, one can determine whether and where the line described by intersects with the circle described by by solving the system of equations made up of these two equations. Topology studies the properties of geometric figures or topological space
In mathematics, a topological space is, roughly speaking, a Geometry, geometrical space in which Closeness (mathematics), closeness is defined but cannot necessarily be measured by a numeric Distance (mathematics), distance. More specifically, a to ...
s that are preserved under operations of continuous deformation. Algebraic topology
Algebraic topology is a branch of mathematics that uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariant (mathematics), invariants that classification theorem, classify topological spaces up t ...
relies on algebraic theories such as group theory
In abstract algebra, group theory studies the algebraic structures known as group (mathematics), groups.
The concept of a group is central to abstract algebra: other well-known algebraic structures, such as ring (mathematics), rings, field ( ...
to classify topological spaces. For example, homotopy groups classify topological spaces based on the existence of loops or holes in them.
Number theory is concerned with the properties of and relations between integers. Algebraic number theory
Algebraic number theory is a branch of number theory that uses the techniques of abstract algebra to study the integers, rational numbers, and their generalizations. Number-theoretic questions are expressed in terms of properties of algebraic ob ...
applies algebraic methods and principles to this field of inquiry. Examples are the use of algebraic expressions to describe general laws, like Fermat's Last Theorem
In number theory, Fermat's Last Theorem (sometimes called Fermat's conjecture, especially in older texts) states that no three positive number, positive integers , , and satisfy the equation for any integer value of greater than . The cases ...
, and of algebraic structures to analyze the behavior of numbers, such as the ring of integers. The related field of combinatorics
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many ...
uses algebraic techniques to solve problems related to counting, arrangement, and combination of discrete objects. An example in algebraic combinatorics is the application of group theory to analyze graphs and symmetries. The insights of algebra are also relevant to calculus, which uses mathematical expressions to examine rates of change and accumulation. It relies on algebra, for instance, to understand how these expressions can be transformed and what role variables play in them. Algebraic logic employs the methods of algebra to describe and analyze the structures and patterns that underlie logical reasoning
Logical reasoning is a mind, mental Action (philosophy), activity that aims to arrive at a Logical consequence, conclusion in a Rigour, rigorous way. It happens in the form of inferences or arguments by starting from a set of premises and reason ...
, exploring both the relevant mathematical structures themselves and their application to concrete problems of logic. It includes the study of Boolean algebra to describe propositional logic as well as the formulation and analysis of algebraic structures corresponding to more complex systems of logic.
Algebraic methods are also commonly employed in other areas, like the natural sciences. For example, they are used to express scientific laws and solve equations in physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, chemistry
Chemistry is the scientific study of the properties and behavior of matter. It is a physical science within the natural sciences that studies the chemical elements that make up matter and chemical compound, compounds made of atoms, molecules a ...
, and biology
Biology is the scientific study of life and living organisms. It is a broad natural science that encompasses a wide range of fields and unifying principles that explain the structure, function, growth, History of life, origin, evolution, and ...
. Similar applications are found in fields like economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and interac ...
, geography
Geography (from Ancient Greek ; combining 'Earth' and 'write', literally 'Earth writing') is the study of the lands, features, inhabitants, and phenomena of Earth. Geography is an all-encompassing discipline that seeks an understanding o ...
, engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
(including electronics
Electronics is a scientific and engineering discipline that studies and applies the principles of physics to design, create, and operate devices that manipulate electrons and other Electric charge, electrically charged particles. It is a subfield ...
and robotics
Robotics is the interdisciplinary study and practice of the design, construction, operation, and use of robots.
Within mechanical engineering, robotics is the design and construction of the physical structures of robots, while in computer s ...
), and computer science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, ...
to express relationships, solve problems, and model systems. Linear algebra plays a central role in artificial intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of re ...
and machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
, for instance, by enabling the efficient processing and analysis of large datasets. Various fields rely on algebraic structures investigated by abstract algebra. For example, physical sciences like crystallography
Crystallography is the branch of science devoted to the study of molecular and crystalline structure and properties. The word ''crystallography'' is derived from the Ancient Greek word (; "clear ice, rock-crystal"), and (; "to write"). In J ...
and quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
make extensive use of group theory, which is also employed to study puzzles such as Sudoku and Rubik's cubes, and origami. Both coding theory
Coding theory is the study of the properties of codes and their respective fitness for specific applications. Codes are used for data compression, cryptography, error detection and correction, data transmission and computer data storage, data sto ...
and cryptology rely on abstract algebra to solve problems associated with data transmission
Data communication, including data transmission and data reception, is the transfer of data, signal transmission, transmitted and received over a Point-to-point (telecommunications), point-to-point or point-to-multipoint communication chann ...
, like avoiding the effects of noise
Noise is sound, chiefly unwanted, unintentional, or harmful sound considered unpleasant, loud, or disruptive to mental or hearing faculties. From a physics standpoint, there is no distinction between noise and desired sound, as both are vibrat ...
and ensuring data security.
Education
secondary education
Secondary education is the education level following primary education and preceding tertiary education.
Level 2 or ''lower secondary education'' (less commonly ''junior secondary education'') is considered the second and final phase of basic e ...
since it requires mastery of the fundamentals of arithmetic while posing new cognitive challenges associated with abstract reasoning and generalization. It aims to familiarize students with the formal side of mathematics by helping them understand mathematical symbolism, for example, how variables can be used to represent unknown quantities. An additional difficulty for students lies in the fact that, unlike arithmetic calculations, algebraic expressions are often difficult to solve directly. Instead, students need to learn how to transform them according to certain laws, often to determine an unknown quantity.
Some tools to introduce students to the abstract side of algebra rely on concrete models and visualizations of equations, including geometric analogies, manipulatives including sticks or cups, and "function machines" representing equations as flow diagrams. One method uses balance scales as a pictorial approach to help students grasp basic problems of algebra. The mass of some objects on the scale is unknown and represents variables. Solving an equation corresponds to adding and removing objects on both sides in such a way that the sides stay in balance until the only object remaining on one side is the object of unknown mass. Word problems are another tool to show how algebra is applied to real-life situations. For example, students may be presented with a situation in which Naomi's brother has twice as many apples as Naomi. Given that both together have twelve apples, students are then asked to find an algebraic equation that describes this situation () and to determine how many apples Naomi has
At the university level, mathematics students encounter advanced algebra topics from linear and abstract algebra. Initial undergraduate courses in linear algebra focus on matrices, vector spaces, and linear maps. Upon completing them, students are usually introduced to abstract algebra, where they learn about algebraic structures like groups, rings, and fields, as well as the relations between them. The curriculum typically also covers specific instances of algebraic structures, such as the systems of rational numbers, the real numbers, and the polynomials.
See also
* * * * * * * * *References
Notes
Citations
Sources
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *External links
{{Authority control