Transcendent angle

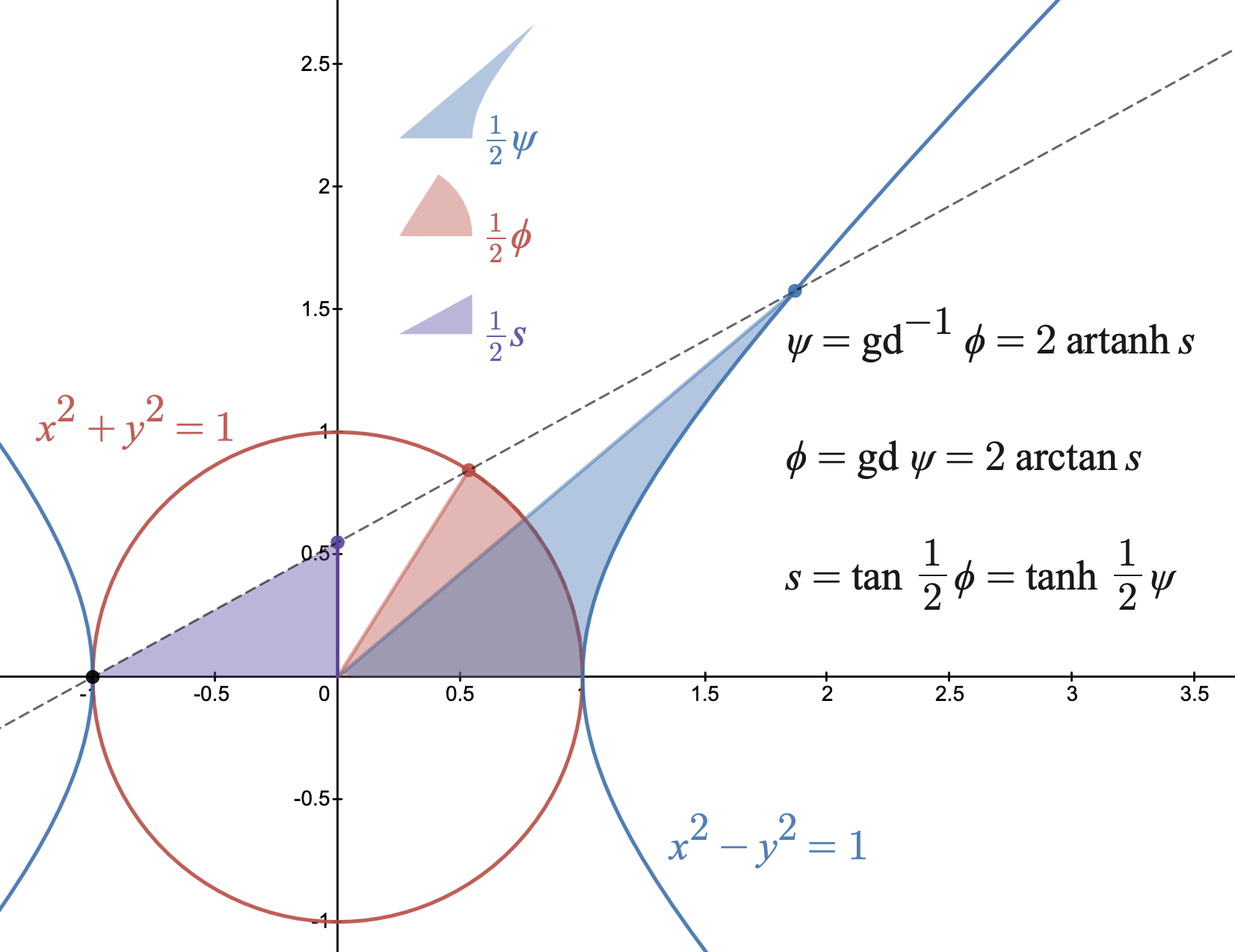In mathematics, the Gudermannian function relates a hyperbolic angle measure $\psi$ to a circular angle measure $\phi$ called the ''gudermannian'' of $\psi$ and denoted $\operatorname\psi$. The Gudermannian function reveals a close relationship between the circular functions and hyperbolic functions. It was introduced in the 1760s by Johann Heinrich Lambert, and later named for Christoph Gudermann who also described the relationship between circular and hyperbolic functions in 1830. The gudermannian is sometimes called the hyperbolic amplitude as a limiting case of the Jacobi elliptic amplitude $\operatorname(\psi, m)$ when parameter $m=1.$

The real Gudermannian function is typically defined for $-\infty < \psi < \infty$ to be the integral of the hyperbolic secant

The real inverse Gudermannian function can be defined for $-\tfrac12\pi < \phi < \tfrac12\pi$ as the integral of the secant

The hyperbolic angle measure $\psi = \operatorname^ \phi$ is called the ''anti-gudermannian'' of $\phi$ or sometimes the lambertian of $\phi$, denoted $\psi = \operatorname \phi.$ In the context of geodesy and navigation for latitude $\phi$, $k \operatorname^ \phi$ (scaled by arbitrary constant $k$) was historically called the meridional part of $\phi$ ( French: ''latitude croissante''). It is the vertical coordinate of the Mercator projection.

The two angle measures $\phi$ and $\psi$ are related by a common stereographic projection

and this identity can serve as an alternative definition for $\operatorname$ and $\operatorname^$ valid throughout the complex plane:

__TOC__

Circular–hyperbolic identities

We can evaluate the integral of the hyperbolic secant using the stereographic projection ( hyperbolic half-tangent) as a change of variables:

Letting $\phi = \operatorname \psi$ and $s = \tan \tfrac12 \phi = \tanh \tfrac12 \psi$ we can derive a number of identities between hyperbolic functions of $\psi$ and circular functions of $\phi.$

These are commonly used as expressions for $\operatorname$ and $\operatorname^$ for real values of $\psi$ and $\phi$ with $, \phi, < \tfrac12\pi.$ For example, the numerically well-behaved formulas

(Note, for $, \phi, > \tfrac12\pi$ and for complex arguments, care must be taken choosing branches of the inverse functions.)

We can also express $\psi$ and $\phi$ in terms of $s\colon$

If we expand $\tan\tfrac12$ and $\tanh\tfrac12$ in terms of the exponential, then we can see that $s,$ $\exp \phi i,$ and $\exp \psi$ are all Möbius transformations of each-other (specifically, rotations of the Riemann sphere):

For real values of $\psi$ and $\phi$ with $, \phi, < \tfrac12\pi$, these Möbius transformations can be written in terms of trigonometric functions in several ways,

These give further expressions for $\operatorname$ and $\operatorname^$ for real arguments with $, \phi, < \tfrac12\pi.$ For example,

Complex values

As a functions of a complex variable, $z \mapsto w = \operatorname z$ conformally maps the infinite strip $\left, \operatornamez\ \leq \tfrac12\pi$ to the infinite strip $\left, \operatornamew\ \leq \tfrac12\pi,$ while $w \mapsto z = \operatorname^ w$ conformally maps the infinite strip $\left, \operatornamew\ \leq \tfrac12\pi$ to the infinite strip $\left, \operatornamez\ \leq \tfrac12\pi.$

Analytically continued by reflections to the whole complex plane, $z \mapsto w = \operatorname z$ is a periodic function of period $2\pi i$ which sends any infinite strip of "height" $2\pi i$ onto the strip $-\pi< \operatornamew \leq \pi.$ Likewise, extended to the whole complex plane, $w \mapsto z = \operatorname^ w$ is a periodic function of period $2\pi$ which sends any infinite strip of "width" $2\pi$ onto the strip $-\pi < \operatornamez \leq \pi.$ For all points in the complex plane, these functions can be correctly written as:

For the $\operatorname$ and $\operatorname^$ functions to remain invertible with these extended domains, we might consider each to be a multivalued function (perhaps $\operatorname$ and $\operatorname^$, with $\operatorname$ and $\operatorname^$ the principal branch) or consider their domains and codomains as Riemann surfaces.

If $u + iv = \operatorname(x + iy),$ then the real and imaginary components $u$ and $v$ can be found by:

(In practical implementation, make sure to use the 2-argument arctangent,

Likewise, if $x + iy = \operatorname^(u + iv),$ then components $x$ and $y$ can be found by:

Multiplying these together reveals the additional identity

Symmetries

The two functions can be thought of as rotations or reflections of each-other, with a similar relationship as $\sinh iz = i \sin z$ between sine and hyperbolic sine:

The functions are both odd and they commute with complex conjugation. That is, a reflection across the real or imaginary axis in the domain results in the same reflection in the codomain:

The functions are periodic, with periods $2\pi i$ and $2\pi$:

A translation in the domain of $\operatorname$ by $\pm\pi i$ results in a half-turn rotation and translation in the codomain by one of $\pm\pi,$ and vice versa for $\operatorname^\colon$

A reflection in the domain of $\operatorname$ across either of the lines $x \pm \tfrac12\pi i$ results in a reflection in the codomain across one of the lines $\pm \tfrac12\pi + yi,$ and vice versa for $\operatorname^\colon$

This is related to the identity

Specific values

A few specific values (where $\infty$ indicates the limit at one end of the infinite strip):

Derivatives

Argument-addition identities

By combining hyperbolic and circular argument-addition identities,

with the circular–hyperbolic identity,

we have the Gudermannian argument-addition identities:

Further argument-addition identities can be written in terms of other circular functions, but they require greater care in choosing branches in inverse functions. Notably,

which can be used to derive the per-component computation for the complex Gudermannian and inverse Gudermannian.

In the specific case $z = w,$ double-argument identities are

Taylor series

The Taylor series near zero, valid for complex values $z$ with $, z, < \tfrac12\pi,$ are

where the numbers $E_$ are the Euler secant numbers, 1, 0, -1, 0, 5, 0, -61, 0, 1385 ... (sequences , , and in the OEIS).

Because the Gudermannian and inverse Gudermannian functions are the integrals of the hyperbolic secant and secant functions, the numerators $E_$ and $, E_,$ are same as the numerators of the Taylor series for and , respectively, but shifted by one place.

The reduced unsigned numerators are 1, 1, 1, 61, 277, ... and the reduced denominators are 1, 6, 24, 5040, 72576, ... (sequences and in the OEIS).

History

The function and its inverse are related to the Mercator projection. The vertical coordinate in the Mercator projection is called isometric latitude, and is often denoted $\psi.$ In terms of latitude $\phi$ on the sphere (expressed in radians) the isometric latitude can be written

The inverse from the isometric latitude to spherical latitude is $\phi = \operatorname \psi.$ (Note: on an ellipsoid of revolution, the relation between geodetic latitude and isometric latitude is slightly more complicated.)

Gerardus Mercator plotted his celebrated map in 1569, but the precise method of construction was not revealed. In 1599, Edward Wright described a method for constructing a Mercator projection numerically from trigonometric tables, but did not produce a closed formula. The closed formula was published in 1668 by James Gregory.

The Gudermannian function per se was introduced by Johann Heinrich Lambert in the 1760s at the same time as the hyperbolic functions. He called it the "transcendent angle," and it went by various names until 1862 when Arthur Cayley suggested it be given its current name as a tribute to Christoph Gudermann's work in the 1830s on the theory of special functions.
Gudermann had published articles in ''Crelle's Journal'' that were later collected in a book
which expounded $\sinh$ and $\cosh$ to a wide audience (although represented by the symbols $\mathfrak$ and $\mathfrak$).

The notation $\operatorname$ was introduced by Cayley who starts by calling $\phi = \operatorname u$ the Jacobi elliptic amplitude $\operatorname u$ in the degenerate case where the elliptic modulus is $m = 1,$ so that $\sqrt$ reduces to $\cos \phi.$ This is the inverse of the integral of the secant function. Using Cayley's notation,

He then derives "the definition of the transcendent",

observing that "although exhibited in an imaginary form, tis a real function of

Generalization

The Gudermannian function can be thought of mapping points on one branch of a hyperbola to points on a semicircle. Points on one sheet of an ''n''-dimensional hyperboloid of two sheets can be likewise mapped onto a ''n''-dimensional hemisphere via stereographic projection. The hemisphere model of hyperbolic space uses such a map to represent hyperbolic space.

Applications

*The angle of parallelism function in hyperbolic geometry is the complement of the gudermannian, $\mathit(\psi) = \tfrac12\pi - \operatorname \psi.$
* On a Mercator projection a line of constant latitude is parallel to the equator (on the projection) and is displaced by an amount proportional to the inverse Gudermannian of the latitude.
* The Gudermannian (with a complex argument) may be used to define the transverse Mercator projection.

* The Gudermannian appears in a non-periodic solution of the inverted pendulum.
* The Gudermannian appears in a moving mirror solution of the dynamical Casimir effect.
* If an infinite number of infinitely long, equidistant, parallel, coplanar, straight wires are kept at equal potentials with alternating signs, the potential-flux distribution in a cross-sectional plane perpendicular to the wires is the complex Gudermannian.
* The Gudermannian function is a sigmoid function, and as such is sometimes used as an activation function in machine learning.
* The (scaled and shifted) Gudermannian is the cumulative distribution function of the hyperbolic secant distribution.
* A function based on the Gudermannian provides a good model for the shape of spiral galaxy
* Catenary#Catenary of equal strength

Notes

External links

* Penn, Michael (2020
"the Gudermannian function!"
on YouTube.

References

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* irst published as *
*
*
*
*
*
*
*
*
*
{{refend

Trigonometry
Elementary special functions
Exponentials