Solenoid (mathematics) on:
[Wikipedia]
[Google]
[Amazon]
:''This page discusses a class of topological groups. For the wrapped loop of wire, see  In mathematics, a solenoid is a compact
In mathematics, a solenoid is a compact

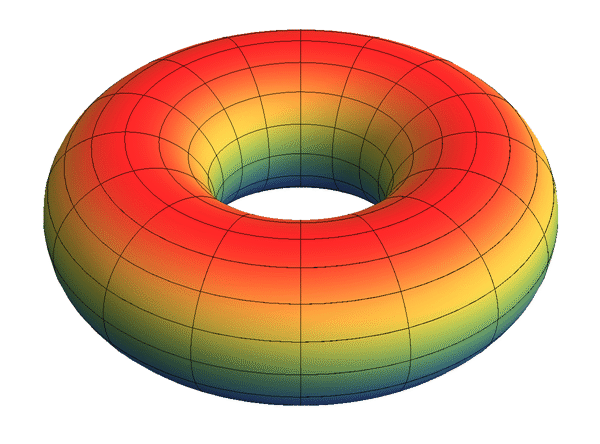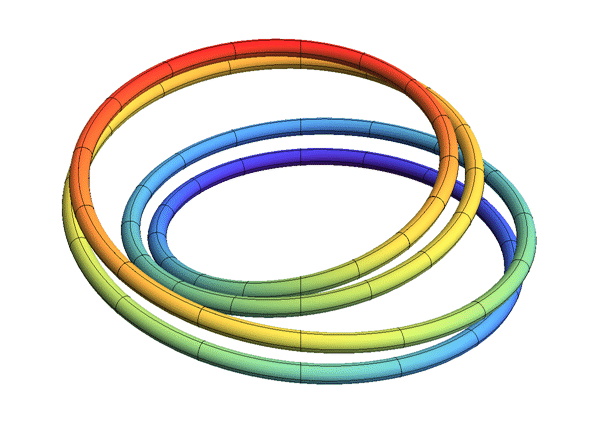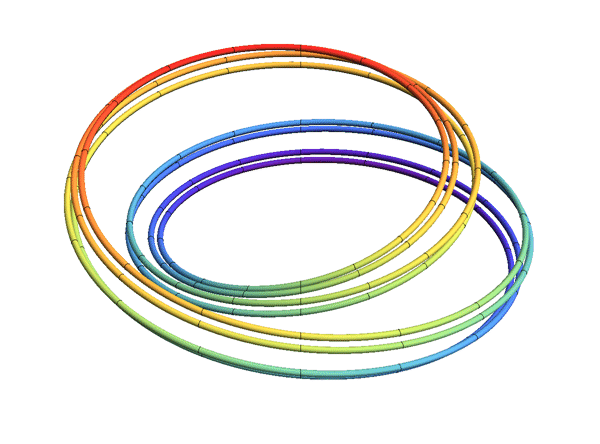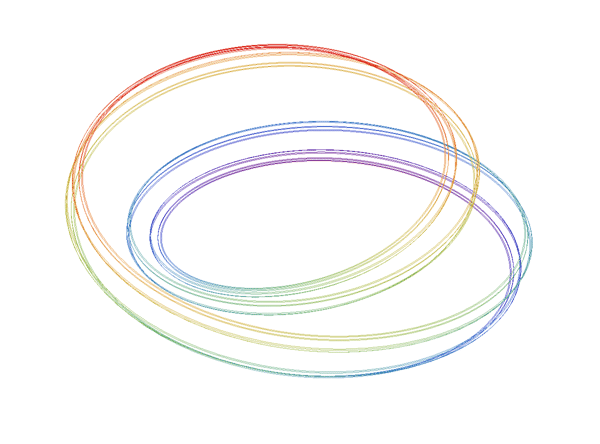 Each solenoid may be constructed as the intersection of a nested system of embedded solid tori in R3.
Fix a sequence of natural numbers , ''n''''i'' ≥ 2. Let ''T''0 = ''S''1 × ''D'' be a solid torus. For each ''i'' ≥ 0, choose a solid torus ''T''''i''+1 that is wrapped longitudinally ''n''''i'' times inside the solid torus ''T''''i''. Then their intersection
:
is homeomorphic to the solenoid constructed as the inverse limit of the system of circles with the maps determined by the sequence .
Here is a variant of this construction isolated by Stephen Smale as an example of an expanding attractor in the theory of smooth dynamical systems. Denote the angular coordinate on the circle ''S''1 by ''t'' (it is defined mod 2π) and consider the complex coordinate ''z'' on the two-dimensional
Each solenoid may be constructed as the intersection of a nested system of embedded solid tori in R3.
Fix a sequence of natural numbers , ''n''''i'' ≥ 2. Let ''T''0 = ''S''1 × ''D'' be a solid torus. For each ''i'' ≥ 0, choose a solid torus ''T''''i''+1 that is wrapped longitudinally ''n''''i'' times inside the solid torus ''T''''i''. Then their intersection
:
is homeomorphic to the solenoid constructed as the inverse limit of the system of circles with the maps determined by the sequence .
Here is a variant of this construction isolated by Stephen Smale as an example of an expanding attractor in the theory of smooth dynamical systems. Denote the angular coordinate on the circle ''S''1 by ''t'' (it is defined mod 2π) and consider the complex coordinate ''z'' on the two-dimensional
''Differentiable dynamical systems''
Bull. of the AMS, 73 (1967), 747 – 817. * L. Vietoris, ''Über den höheren Zusammenhang kompakter Räume und eine Klasse von zusammenhangstreuen Abbildungen'', Math. Ann. 97 (1927), pp. 454–472 * Robert F. Williams
''Expanding attractors''
Publ. Math. IHES, t. 43 (1974), p. 169–203
Solenoid
upright=1.20, An illustration of a solenoid
upright=1.20, Magnetic field created by a seven-loop solenoid (cross-sectional view) described using field lines
A solenoid () is a type of electromagnet formed by a helix, helical coil of wire whose ...
.''
 In mathematics, a solenoid is a compact
In mathematics, a solenoid is a compact connected
Connected may refer to:
Film and television
* ''Connected'' (2008 film), a Hong Kong remake of the American movie ''Cellular''
* '' Connected: An Autoblogography About Love, Death & Technology'', a 2011 documentary film
* ''Connected'' (2015 TV ...
topological space
In mathematics, a topological space is, roughly speaking, a geometrical space in which closeness is defined but cannot necessarily be measured by a numeric distance. More specifically, a topological space is a set whose elements are called po ...
(i.e. a continuum) that may be obtained as the inverse limit of an inverse system of topological groups and continuous homomorphisms
:
where each is a circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is con ...
and ''f''''i'' is the map that uniformly wraps the circle for times () around the circle . This construction can be carried out geometrically in the three-dimensional Euclidean space R3. A solenoid is a one-dimensional homogeneous indecomposable continuum that has the structure of a compact topological group.
Solenoids were first introduced by Vietoris for the case, and by van Dantzig the case, where is fixed. Such a solenoid arises as a one-dimensional expanding attractor, or Smale–Williams attractor, and forms an important example in the theory of hyperbolic
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry.
The following phenomena are described as ''hyperbolic'' because they ...
dynamical system
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in ...
s.
Construction
Geometric construction and the Smale–Williams attractor

 Each solenoid may be constructed as the intersection of a nested system of embedded solid tori in R3.
Fix a sequence of natural numbers , ''n''''i'' ≥ 2. Let ''T''0 = ''S''1 × ''D'' be a solid torus. For each ''i'' ≥ 0, choose a solid torus ''T''''i''+1 that is wrapped longitudinally ''n''''i'' times inside the solid torus ''T''''i''. Then their intersection
:
is homeomorphic to the solenoid constructed as the inverse limit of the system of circles with the maps determined by the sequence .
Here is a variant of this construction isolated by Stephen Smale as an example of an expanding attractor in the theory of smooth dynamical systems. Denote the angular coordinate on the circle ''S''1 by ''t'' (it is defined mod 2π) and consider the complex coordinate ''z'' on the two-dimensional
Each solenoid may be constructed as the intersection of a nested system of embedded solid tori in R3.
Fix a sequence of natural numbers , ''n''''i'' ≥ 2. Let ''T''0 = ''S''1 × ''D'' be a solid torus. For each ''i'' ≥ 0, choose a solid torus ''T''''i''+1 that is wrapped longitudinally ''n''''i'' times inside the solid torus ''T''''i''. Then their intersection
:
is homeomorphic to the solenoid constructed as the inverse limit of the system of circles with the maps determined by the sequence .
Here is a variant of this construction isolated by Stephen Smale as an example of an expanding attractor in the theory of smooth dynamical systems. Denote the angular coordinate on the circle ''S''1 by ''t'' (it is defined mod 2π) and consider the complex coordinate ''z'' on the two-dimensional unit disk
In mathematics, the open unit disk (or disc) around ''P'' (where ''P'' is a given point in the plane), is the set of points whose distance from ''P'' is less than 1:
:D_1(P) = \.\,
The closed unit disk around ''P'' is the set of points whose ...
''D''. Let ''f'' be the map of the solid torus ''T'' = ''S''1 × ''D'' into itself given by the explicit formula
:
This map is a smooth embedding of ''T'' into itself that preserves the foliation
In mathematics (differential geometry), a foliation is an equivalence relation on an ''n''-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension ''p'', modeled on the decomposition of ...
by meridional disks (the constants 1/2 and 1/4 are somewhat arbitrary, but it is essential that 1/4 < 1/2 and 1/4 + 1/2 < 1). If ''T'' is imagined as a rubber tube, the map ''f'' stretches it in the longitudinal direction, contracts each meridional disk, and wraps the deformed tube twice inside ''T'' with twisting, but without self-intersections. The hyperbolic set ''Λ'' of the discrete dynamical system (''T'', ''f'') is the intersection of the sequence of nested solid tori described above, where ''T''''i'' is the image of ''T'' under the ''i''th iteration of the map ''f''. This set is a one-dimensional (in the sense of topological dimension
In mathematics, the Lebesgue covering dimension or topological dimension of a topological space is one of several different ways of defining the dimension of the space in a
topologically invariant way.
Informal discussion
For ordinary Euclidean ...
) attractor
In the mathematical field of dynamical systems, an attractor is a set of states toward which a system tends to evolve, for a wide variety of starting conditions of the system. System values that get close enough to the attractor values remain ...
, and the dynamics of ''f'' on ''Λ'' has the following interesting properties:
* meridional disks are the stable manifolds, each of which intersects ''Λ'' over a Cantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.
T ...
* periodic points of ''f'' are dense
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematicall ...
in ''Λ''
* the map ''f'' is topologically transitive on ''Λ''
General theory of solenoids and expanding attractors, not necessarily one-dimensional, was developed by R. F. Williams and involves a projective system of infinitely many copies of a compact branched manifold in place of the circle, together with an expanding self- immersion.
Construction in toroidal coordinates
In the toroidal coordinates with radius , the solenoid can be parametrized by aswhere Here, are adjustable shape-parameters, with constraint . In particular, works. Let be the solenoid constructed this way, then the topology of the solenoid is just the subset topology induced by the Euclidean topology on . Since the parametrization is bijective, we can pullback the topology on to , which makes itself the solenoid. This allows us to construct the inverse limit maps explicitly:Construction by symbolic dynamics
Viewed as a set, the solenoid is just a Cantor-continuum of circles, wired together in a particular way. This suggests to us the construction by symbolic dynamics, where we start with a circle as a "racetrack", and append an "odometer" to keep track of which circle we are on. Define as the solenoid. Next, define addition on the odometer , in the same way as p-adic numbers. Next, define addition on the solenoid byThe topology on the solenoid is generated by the basis containing the subsets , where is any open interval in , and is the set of all elements of starting with the initial segment .Pathological properties
Solenoids are compact metrizable spaces that areconnected
Connected may refer to:
Film and television
* ''Connected'' (2008 film), a Hong Kong remake of the American movie ''Cellular''
* '' Connected: An Autoblogography About Love, Death & Technology'', a 2011 documentary film
* ''Connected'' (2015 TV ...
, but not locally connected or path connected
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint non-empty open subsets. Connectedness is one of the principal topological properties t ...
. This is reflected in their pathological
Pathology is the study of the causes and effects of disease or injury. The word ''pathology'' also refers to the study of disease in general, incorporating a wide range of biology research fields and medical practices. However, when used in th ...
behavior with respect to various homology theories
In mathematics, homology is a general way of associating a sequence of algebraic objects, such as abelian groups or modules, with other mathematical objects such as topological spaces. Homology groups were originally defined in algebraic topol ...
, in contrast with the standard properties of homology for simplicial complexes. In Čech homology, one can construct a non-exact long homology sequence using a solenoid. In Steenrod-style homology theories, the 0th homology group of a solenoid may have a fairly complicated structure, even though a solenoid is a connected space.
See also
*Protorus
In mathematics, a protorus is a compact connected topological abelian group. Equivalently, it is a projective limit of tori (products of a finite number of copies of the circle group), or the Pontryagin dual of a discrete torsion-free abelian gr ...
, a class of topological groups that includes the solenoids
* Pontryagin duality
* Inverse limit
* p-adic number
* Profinite integer
References
* D. van Dantzig, ''Ueber topologisch homogene Kontinua'', Fund. Math. 15 (1930), pp. 102–125 * * Clark Robinson, ''Dynamical systems: Stability, Symbolic Dynamics and Chaos'', 2nd edition, CRC Press, 1998 * S. Smale''Differentiable dynamical systems''
Bull. of the AMS, 73 (1967), 747 – 817. * L. Vietoris, ''Über den höheren Zusammenhang kompakter Räume und eine Klasse von zusammenhangstreuen Abbildungen'', Math. Ann. 97 (1927), pp. 454–472 * Robert F. Williams
''Expanding attractors''
Publ. Math. IHES, t. 43 (1974), p. 169–203
Further reading
* {{DEFAULTSORT:Solenoid (Mathematics) Topological groups Continuum theory Algebraic topology Ring theory Number theory P-adic numbers