nephroid

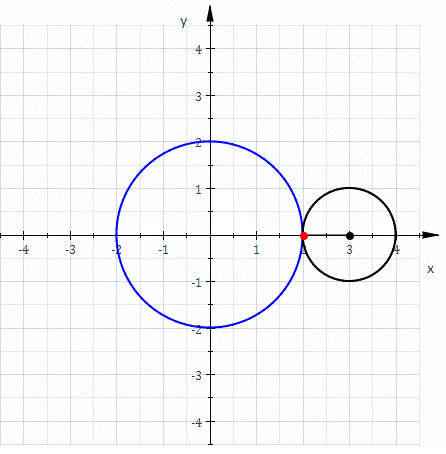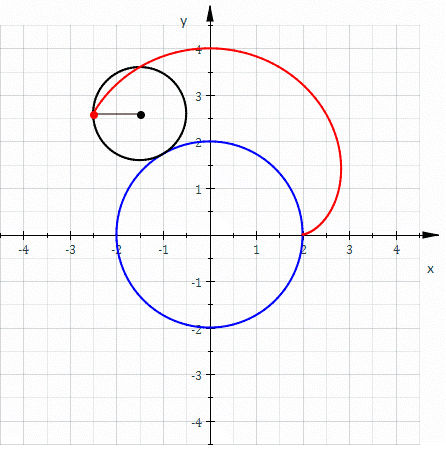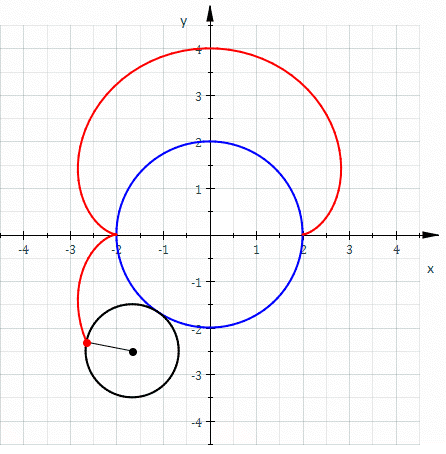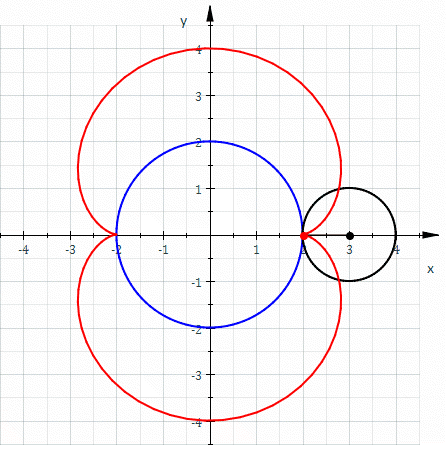
In geometry, a nephroid () is a specific plane curve. It is a type of epicycloid in which the smaller circle's radius differs from the larger by a factor of one-half.

Name

Although the term ''nephroid'' was used to describe other curves, it was applied to the curve in this article by Richard A. Proctor in 1878.

Strict definition

A nephroid is
* an algebraic curve of degree 6.
* an epicycloid with two cusps
* a plane simple closed curve = a Jordan curve

Equations

Parametric

If the small circle has radius $a$, the fixed circle has midpoint $(0,0)$ and radius $2a$, the rolling angle of the small circle is $2\varphi$ and point $(2a,0)$ the starting point (see diagram) then one gets the parametric representation:
:$x(\varphi) = 3a\cos\varphi- a\cos3\varphi=6a\cos\varphi-4a \cos^3\varphi \ ,$
:$y(\varphi) = 3a \sin\varphi - a\sin3\varphi =4a\sin^3\varphi\ , \qquad 0\le \varphi < 2\pi$

The complex map $z \to z^3 + 3z$ maps the unit circle to a nephroidMathematical Documentation of the objects realized in the visualization program 3D-XplorMath
/ref>

=Proof of the parametric representation

=
The proof of the parametric representation is easily done by using complex numbers and their representation as complex plane. The movement of the small circle can be split into two rotations. In the complex plane a rotation of a point $z$ around point $0$ (origin) by an angle $\varphi$ can be performed by the multiplication of point $z$ (complex number) by $e^$. Hence the
:rotation $\Phi_3$ around point $3a$ by angle $2\varphi$ is $: z \mapsto 3a+(z-3a)e^$ ,
:rotation $\Phi_0$ around point $0$ by angle $\varphi$ is $:\quad z \mapsto ze^$.

A point $p(\varphi)$ of the nephroid is generated by the rotation of point $2a$ by $\Phi_3$ and the subsequent rotation with $\Phi_0$:
:$p(\varphi)=\Phi_0(\Phi_3(2a))=\Phi_0(3a-ae^)=(3a-ae^)e^=3ae^-ae^$.
Herefrom one gets
:$\begin x(\varphi)&=&3a\cos\varphi-a\cos3\varphi &=& 6a\cos\varphi-4a \cos^3\varphi \ ,&& \\ y(\varphi)&=&3a\sin\varphi-a\sin3\varphi&=& 4a\sin^3\varphi &.& \end$
(The formulae $e^=\cos\varphi+ i\sin\varphi, \ \cos^2\varphi+ \sin^2\varphi=1, \ \cos3\varphi=4\cos^3\varphi-3\cos\varphi,\;\sin 3\varphi=3\sin\varphi -4\sin^3\varphi$ were used. See trigonometric functions.)

Implicit

Inserting $x(\varphi)$ and $y(\varphi)$ into the equation
*$(x^2+y^2-4a^2)^3=108a^4y^2$
shows that this equation is an implicit representation of the curve.

=Proof of the implicit representation

=
With
:$x^2+y^2-4a^2=(3a\cos\varphi-a\cos3\varphi)^2+(3a\sin\varphi-a\sin3\varphi)^2 -4a^2=\cdots=6a^2(1-\cos2\varphi)=12a^2\sin^2\varphi$
one gets
:$(x^2+y^2-4a^2)^3=(12a^2)^3\sin^6\varphi=108a^4(4a\sin^3\varphi)^2=108a^4y^2\ .$

Orientation

If the cusps are on the y-axis the parametric representation is
:$x=3a\cos \varphi+a\cos3\varphi,\quad y=3a\sin \varphi+a\sin3\varphi).$
and the implicit one:
:$(x^2+y^2-4a^2)^3=108a^4x^2.$

Metric properties

For the nephroid above the
* arclength is $L= 24 a,$
*area $A= 12\pi a^2\$ and
*radius of curvature is $\rho=, 3a\sin \varphi, .$
The proofs of these statements use suitable formulae on curves (arc length, area and radius of curvature) and the parametric representation above
:$x(\varphi)=6a\cos\varphi-4a \cos^3\varphi \ ,$
:$y(\varphi)= 4a\sin^3\varphi$
and their derivatives
:$\dot x=-6a\sin\varphi(1 - 2\cos^2\varphi)\ ,\quad \ \ddot x= -6 a\cos \varphi(5-6\cos^2\varphi)\ ,$
:$\dot y=12a\sin^2\varphi\cos\varphi \quad , \quad \quad \quad \quad \ddot y=12a\sin\varphi(3\cos^2\varphi-1)\ .$

;Proof for the arc length:
:$L=2\int_0^\pi \; d\varphi=\cdots =12a\int_0^\pi \sin\varphi\; d\varphi= 24a$ .

;Proof for the area:
: A=2\cdot \tfrac, \int_0^\pi \dot y-y \dot x; d\varphi, =\cdots= 24a^2\int_0^\pi\sin^2\varphi\; d\varphi= 12\pi a^2 .

;Proof for the radius of curvature:
:$\rho = \left, \frac \=\cdots= , 3a\sin \varphi, .$

Construction

* It can be generated by rolling a circle with radius $a$ on the outside of a fixed circle with radius $2a$. Hence, a nephroid is an epicycloid.

Nephroid as envelope of a pencil of circles

*Let be $c_0$ a circle and $D_1,D_2$ points of a diameter $d_$, then the envelope of the pencil of circles, which have midpoints on $c_0$ and are touching $d_$ is a ''nephroid'' with cusps $D_1,D_2$.

Proof

Let $c_0$ be the circle $(2a\cos\varphi,2a\sin\varphi)$ with midpoint $(0,0)$ and radius $2a$. The diameter may lie on the x-axis (see diagram). The pencil of circles has equations:
:$f(x,y,\varphi)=(x-2a\cos\varphi)^2+(y-2a\sin\varphi)^2-(2a\sin\varphi)^2=0 \ .$
The envelope condition is
:$f_\varphi(x,y,\varphi)=2a(x\sin\varphi -y\cos\varphi-2a\cos\varphi\sin\varphi)=0\ .$
One can easily check that the point of the nephroid $p(\varphi)=(6a\cos\varphi-4a \cos^3\varphi\; ,\; 4a\sin^3\varphi)$ is a solution of the system $f(x,y,\varphi)=0, \; f_\varphi(x,y,\varphi)=0$ and hence a point of the envelope of the pencil of circles.

Nephroid as envelope of a pencil of lines

Similar to the generation of a cardioid as envelope of a pencil of lines the following procedure holds:
# Draw a circle, divide its perimeter into equal spaced parts with $3N$ points (see diagram) and number them consecutively.
# Draw the chords: $(1,3), (2,6), ...., (n,3n),...., (N,3N), (N+1,3), (N+2,6), ....,$. (i.e.: The second point is moved by threefold velocity.)
# The ''envelope'' of these chords is a nephroid.

Proof

The following consideration uses trigonometric formulae for
$\cos \alpha+\cos\beta,\ \sin \alpha+\sin\beta, \ \cos (\alpha+\beta), \ \cos2\alpha$. In order to keep the calculations simple, the proof is given for the nephroid with cusps on the y-axis.
''Equation of the tangent'': for the nephroid with parametric representation
:$x=3\cos\varphi + \cos3\varphi,\; y=3\sin\varphi+\sin3\varphi$:
Herefrom one determines the normal vector $\vec n=(\dot y , -\dot x)^T$, at first.


The equation of the tangent $\dot y(\varphi)\cdot (x -x(\varphi)) - \dot x(\varphi)\cdot (y-y(\varphi))= 0$ is:
:$(\cos2\varphi\cdot x \ + \ \sin 2\varphi\cdot y)\cos \varphi = 4\cos^2 \varphi \ .$
For $\varphi=\tfrac,\tfrac$ one gets the cusps of the nephroid, where there is no tangent. For $\varphi\ne\tfrac,\tfrac$ one can divide by $\cos\varphi$ to obtain
*$\cos2\varphi \cdot x + \sin2\varphi \cdot y = 4 \cos\varphi \ .$

''Equation of the chord'': to the circle with midpoint $(0,0)$ and radius $4$: The equation of the chord containing the two points $(4\cos\theta, 4\sin\theta), \ (4\cos\theta, 4\sin\theta))$ is:
:$(\cos2\theta \cdot x + \sin2\theta \cdot y)\sin\theta = 4 \cos\theta\sin\theta \ .$
For $\theta =0, \pi$ the chord degenerates to a point. For $\theta \ne 0,\pi$ one can divide by $\sin\theta$ and gets the equation of the chord:
*$\cos2\theta \cdot x + \sin2\theta \cdot y = 4 \cos\theta \ .$
The two angles $\varphi , \theta$ are defined differently ($\varphi$ is one half of the rolling angle, $\theta$ is the parameter of the circle, whose chords are determined), for $\varphi=\theta$ one gets the same line. Hence any chord from the circle above is tangent to the nephroid and
* ''the nephroid is the envelope of the chords of the circle.''

Nephroid as caustic of one half of a circle

The considerations made in the previous section give a proof for the fact, that the caustic of one half of a circle is a nephroid.

* If in the plane parallel light rays meet a reflecting half of a circle (see diagram), then the reflected rays are tangent to a nephroid.

Proof

The circle may have the origin as midpoint (as in the previous section) and its
radius is $4$. The circle has the parametric representation
:$k(\varphi)=4(\cos\varphi,\sin\varphi) \ .$
The tangent at the circle point $K:\ k(\varphi)$ has normal vector $\vec n_t=(\cos\varphi,\sin\varphi)^T$. The reflected ray has the normal vector (see diagram) $\vec n_r=(\cos\varphi,\sin\varphi)^T$ and containing circle point $K: \ 4(\cos\varphi,\sin\varphi)$. Hence the reflected ray is part of the line with equation
:$\cos\varphi\cdot x \ + \ \sin \varphi\cdot y = 4\cos\varphi \ ,$
which is tangent to the nephroid of the previous section at point
:$P:\ (3\cos\varphi + \cos3\varphi,3\sin\varphi+\sin3\varphi)$ (see above).

The evolute and involute of a nephroid

Evolute

The evolute of a curve is the locus of centers of curvature. In detail: For a curve $\vec x=\vec c(s)$ with radius of curvature $\rho(s)$ the evolute has the representation
:$\vec x=\vec c(s) + \rho(s)\vec n(s).$
with $\vec n(s)$ the suitably oriented unit normal.

For a nephroid one gets:
*The ''evolute'' of a nephroid is another nephroid half as large and rotated 90 degrees (see diagram).

Proof

The nephroid as shown in the picture has the parametric representation
:$x=3\cos\varphi + \cos3\varphi,\quad y=3\sin\varphi+\sin3\varphi \ ,$
the unit normal vector pointing to the center of curvature
:$\vec n(\varphi)=(-\cos 2\varphi,-\sin 2\varphi)^T$ (see section above)
and the radius of curvature $3\cos \varphi$ (s. section on metric properties).
Hence the evolute has the representation:
:$x=3\cos\varphi + \cos3\varphi -3\cos\varphi\cdot\cos2\varphi=\cdots=3\cos\varphi-2\cos^3\varphi,$
:$y=3\sin\varphi+\sin3\varphi -3\cos\varphi\cdot\sin2\varphi\ =\cdots=2\sin^3\varphi \ ,$
which is a nephroid half as large and rotated 90 degrees (see diagram and section above)

Involute

Because the evolute of a nephroid is another nephroid, the involute of the nephroid is also another nephroid. The original nephroid in the image is the involute of the smaller nephroid.

Inversion of a nephroid

The inversion
:$x \mapsto \frac, \quad y\mapsto \frac$
across the circle with midpoint $(0,0)$ and radius $2a$ maps the nephroid with equation
:$(x^2+y^2-4a^2)^3=108a^4y^2$
onto the curve of degree 6 with equation
: $(4a^2-(x^2+y^2))^3=27a^2(x^2+y^2)y^2$ (see diagram) .

References

*Arganbright, D., ''Practical Handbook of Spreadsheet Curves and Geometric Constructions'', CRC Press, 1939, , p. 54.
* Borceux, F., ''A Differential Approach to Geometry: Geometric Trilogy III'', Springer, 2014, , p. 148.
*Lockwood, E. H., ''A Book of Curves,'' Cambridge University Press, 1961, , p. 7.

External links

{{Commonscat, Nephroid

Mathworld: nephroid



Roulettes (curve)